рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Электроника
- /
- ОРТОГОНАЛЬНЫЕ ПЕРИОДИЧЕСКИЕ ФУНКЦИИ
Реферат Курсовая Конспект
ОРТОГОНАЛЬНЫЕ ПЕРИОДИЧЕСКИЕ ФУНКЦИИ
ОРТОГОНАЛЬНЫЕ ПЕРИОДИЧЕСКИЕ ФУНКЦИИ - раздел Электроника, ПРЕДСТАВЛЕНИЕ МОДЕЛИ, ИСПОЛЬЗУЮЩЕЕ СЛУЧАЙНЫЕ ИМПУЛЬСЫ Тригонометрические Функции ...
Тригонометрические функции 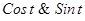 являются периодическими с периодом
являются периодическими с периодом 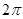 , т.е.
, т.е.
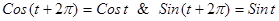 (1)
(1)
Отсюда следует, что
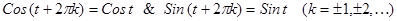 (2)
(2)
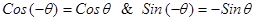
Мы можем линейно преобразовать аргументы, сохранив свойство периодичности. Функции 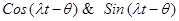 периодичны с периодом
периодичны с периодом 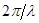 , т.е.
, т.е.
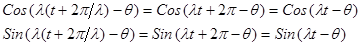 (3)
(3)
Обратная величина 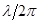 называется частотой. Она равна числу периодов (не обязательно целому), содержащемуся в единичном интервале.
называется частотой. Она равна числу периодов (не обязательно целому), содержащемуся в единичном интервале.
Иными словами, именно такое число раз функция повторяет свои значения. Умножение на 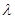 соответствует вычитание
соответствует вычитание 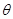 - сдвигу графика косинуса или синуса. Функция
- сдвигу графика косинуса или синуса. Функция 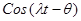 достигает максимума в точках
достигает максимума в точках 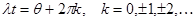 , т.е. при
, т.е. при 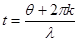 .
.
Угол 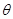 называется фазой. Обычно
называется фазой. Обычно 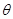 выбирается так, чтобы первый max достигался в точке
выбирается так, чтобы первый max достигался в точке 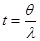 . В таком случае
. В таком случае 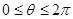 .
.
При t=0 указанные тригонометрические функции равны, соответственно 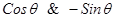 .
.
Сдвинутые косинусоида и синусоида являются линейными комбинациями обычной косинусоиды и обычной синусоиды и наоборот. Из тригонометрической формулы 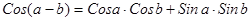 имеем
имеем
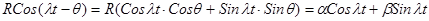 (4)
(4)
где 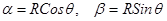 (5)
(5)
или, что эквивалентно, 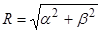
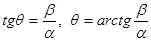 (6)
(6)
Коэффициент R, являющийся максимумом функции 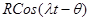 , называется амплитудой этой функции. Выражение (4) можно записать также в виде
, называется амплитудой этой функции. Выражение (4) можно записать также в виде 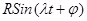 , где
, где 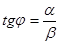 , но обычно предпочитают использовать функцию косинус.
, но обычно предпочитают использовать функцию косинус.
С тригонометрическими функциями довольно удобно работать вследствие того, что они обладают определенными свойствами ортогональности.
Мы рассмотрим здесь свойства ортогональности сумм на множестве 1,…,T. Рассмотрим частоты 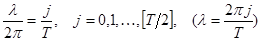 , где
, где
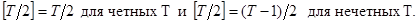
(недостающую единицу принимают за 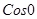 )
)
Период при этом равен 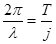 . Функции косинус и синус с такими частотами являются ортогональными. Чтобы показать это, удобно воспользоваться соотношениями:
. Функции косинус и синус с такими частотами являются ортогональными. Чтобы показать это, удобно воспользоваться соотношениями:
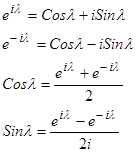 (7)
(7)
При этом
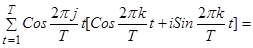 (8)
(8)
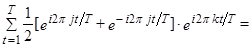 (
(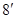 )
)
=изменяем (сдвигаем) пределы суммирования – от 0 до (Т-1), а в формулах вместо t подставим (t+1), чтобы ничего не изменилось=
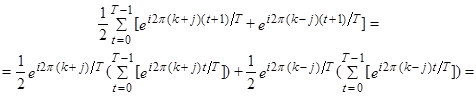
(т.к.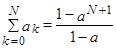 )
)
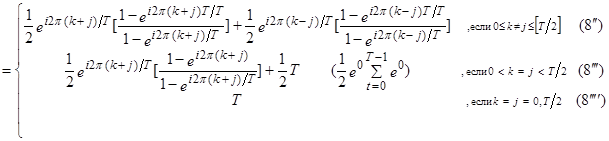
Покажем справедливость (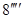 )
)
Действительно, при k=j=0 имеем из (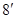 ):
):
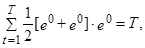
при 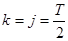 из (8)
из (8)
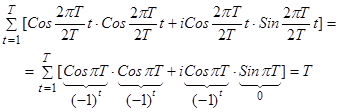
Далее, покажем, что (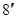 )=0
)=0
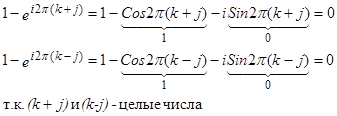
Следовательно, и 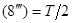
Итак, получаем:
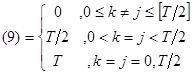
Приравнивая действительные и мнимые части в соотношении (8), с учетом того, что в (9) нет мнимых частей), получаем:
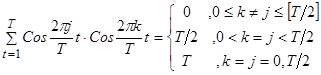 (10)
(10)
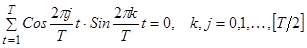 (11)
(11)
Подобным же образом можно показать, что
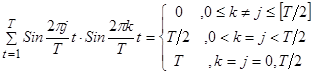 (12)
(12)
Кроме того, полагая j=0 в (10) и (11), получаем:
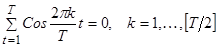 (13)
(13)
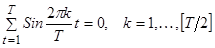 (14)
(14)
Если Т – нечетное, то 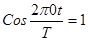 .
.
При этом 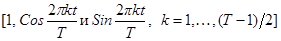 образуют множество из Т последовательностей по Т чисел, любые две из которых ортогональны.
образуют множество из Т последовательностей по Т чисел, любые две из которых ортогональны.
Если Т – четное, то таким множеством является совокупность функций 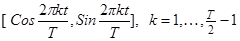 и
и 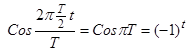 . Сумма квадратов членов каждой последовательности равна
. Сумма квадратов членов каждой последовательности равна 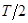 , за исключением последовательностей 1 и (-1), у которых она равна Т.
, за исключением последовательностей 1 и (-1), у которых она равна Т.
– Конец работы –
Эта тема принадлежит разделу:
ПРЕДСТАВЛЕНИЕ МОДЕЛИ, ИСПОЛЬЗУЮЩЕЕ СЛУЧАЙНЫЕ ИМПУЛЬСЫ
На сайте allrefs.net читайте: "ПРЕДСТАВЛЕНИЕ МОДЕЛИ, ИСПОЛЬЗУЮЩЕЕ СЛУЧАЙНЫЕ ИМПУЛЬСЫ"...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: ОРТОГОНАЛЬНЫЕ ПЕРИОДИЧЕСКИЕ ФУНКЦИИ
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов