Математические модели финансовой математики носят вероятностный характер
Часть 1. Теория вероятностей
Тема: Элементы теории вероятностей
Математические модели финансовой математики носят вероятностный характер.
Теория вероятностей является разделом математики, в котором изучаются математические модели случайных экспериментов, исходы которых нельзя определить однозначно условиями проведения опыта. При этом предполагается, что сам эксперимент может быть повторен (хотя бы в принципе) любое число раз при неизменном комплексе условий, а исходы эксперимента обладают статистической устойчивостью.
Например, 1) при однократном подбрасывании монеты возможны следующие исходы (события): выпадение «герба» или «решки». В результате проведения опыта возникает лишь один исход, однако, до проведения опыта нельзя установить какой; 2) проводя контроль качества деталей, так же возможны два исхода: не бракованная или бракованная. Однако до проведения опыта опять же нельзя сказать, какой исход будет установлен для каждой детали; 3) предположим, нас интересует число вызовов, которое поступит за определенный промежуток времени на телефонную станцию. Как и в предыдущих примерах, интересующую величину до проведения эксперимента определить невозможно, хотя очевидно, что результатом будет целое неотрицательное число.
Примеров такого рода можно привести сколь угодно. Принято говорить, что возникающее в ходе эксперимента событие (исход) является случайным.
В чем состоит общность опытов со случайными исходами? Оказывается, несмотря на то, что результат каждого из перечисленных выше экспериментов предсказать невозможно, на практике уже давно была замечена закономерность: при проведении большого количества испытаний наблюденные частоты появления каждого случайного события (это отношение числа его появлений к общему числу испытаний) стабилизируются, то есть все меньше отличаются от некоторого числа, называемого вероятностью события. Так, при многократном бросании игральной кости «шестерка» выпадает в среднем в каждом шестом случае. Такое свойство устойчивости частоты позволяет, не имея возможности предсказать исход отдельного опыта, достаточно точно прогнозировать свойства явлений, связанных с рассматриваемым опытом. Поэтому методы теории вероятностей в современной жизни проникли во все сферы деятельности человека, причем не только в естественно-научные, экономические, но и гуманитарные (например, историю, лингвистику и т.д.).
Вероятность события
Обозначим число благоприятствующих событию А исходов через М, а число всех исходов — N: P(A)=M/N, где М — целое неотрицательное число, 0 £ М £ N.Правила сложения и умножения вероятностей.
Зависимые и независимые события
Р(А + В) = Р(А) + Р(В) - Р(АВ). Для несовместных событий их совместное наступление есть невозможное событие,…Формула полной вероятности и формула Байеса
Пусть событие А может осуществиться лишь вместе с одним из событий Н1, Н2, H3, ..., Hn, образующих полную группу. Пусть известны вероятности Р(Н1),… а также известны и условные вероятности события А:Случайные величины и законы их распределения
Величину называют случайной, если в результате испытания она примет лишь одно возможное значение, заранее неизвестное и зависящее от случая. В теории вероятностей и на практике случайной величиной называют функцию,… Примеры случайных величин: количество гербов, выпавших при независимом бросании двух монет, число, выпавшее на верхней…Дискретные случайные величины (ДСВ) и законы их распределения
Способы задания дискретной случайной величины.
1. Для задания дискретной случайной величины необходимо задать вероятностное простpанство <Ω,Σ,p>. В дискретном случае это означает. что тем или иным способом должны быть перечислены все возможные значения случайной величины и соответствующие им вероятности появления этих значений.
Если случайная величина Х принимает значения х1,х2,….хn соответственно с вероятностями p1,p2,…pn и при этом х1<х2<….<хn и 
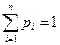 , то таблица
, то таблица
| Х | х1 | x2 | … | xi | … | xn |
| Р | p1 | p2 | … | pi | … | pn |
называется законом распределения вероятностей или рядом распределения случайной величины.
2. 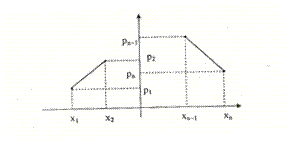 График распределения вероятностей дискретной случайной величины называют полигоном или многоугольником распределения вероятностей.
График распределения вероятностей дискретной случайной величины называют полигоном или многоугольником распределения вероятностей.
Числовые характеристики дискретной случайной величины.
Основные меры положения ДСВ. 1. Мода – самое вероятное значение случайной величины (абсцисса самой высокой точки полигона вероятностей). ДСВ может…Законы распределения ДСВ.
Биномиальное распределение.
1) Каждое испытание имеет 2 исхода, называемые успех и неуспех; это – взаимно несовместные и противоположные события; 2) Вероятность успеха – р – остается постоянной от испытания к испытанию;… 3) Все n испытаний – независимы. Это означает, что вероятность наступления события в любом из n повторных испытаний…Гипергеометрическое распределение.
Пусть во множестве из N элементов содержится k элементов с признаком В. Вероятность выбрать элемент с признаком В при одном случайном извлечении из… Замечание. В отличии от биномиального закона, применимого в случае независимых… Вероятность появления в выборке из n элементов ровно х элементов с признаком В вычисляется по формуле: .Распределение Пуассона.
Распределение Пуассона можно описать с помощью следующей математической модели. Пусть событие А происходит многократно с течением времени, то есть… 1) Поток стационарен, то есть вероятность попадания k событий в промежуток… 2) Поток без последствия, то есть вероятность попадания k событий в промежуток времени (t; t+τ) не зависит от…Непрерывные случайные величины (НСВ) и законы их распределения.
Способы задания НСВ.
Напомним, что случайная величина называется непрерывной, если множеством ее значений является интервал.
Для исследования вероятностных свойств СВ необходимо знать правило, позволяющее находить вероятность того, что СВ примет значение из подмножества ее значений. Для НСВ нельзя определить вероятность того, что она примет некоторое конкретное значение (точечную вероятность). Так как в любом интервале содержится бесконечно много значений, то вероятность выпадения одного из них асимптотически равна нулю. В результате НСВ нельзя задать таблицей. Для описания НСВ используют так называемую функцию распределения.
Определение. Функцией распределения F(x) называется вероятность того, что случайная величина Х примет значение меньшее некоторого заданного х., т.е. 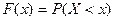 .
.
Определение. Случайная величина называется абсолютно непрерывной, если ее функция распределения может быть представлена в виде: 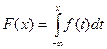 .
.
F(х) непрерывна, как функция верхнего предела интегрирования. Функция f(x) (подынтегральная функция в формуле для F(x)) называется функцией плотности вероятности (это вероятность, приходящаяся на единицу длины в данной точке). Таким образом. 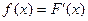 . В связи с этим, функцию F(x) называют интегральным законом распределения СВ Х, а f(x) – дифференциальным законом распределения СВ.
. В связи с этим, функцию F(x) называют интегральным законом распределения СВ Х, а f(x) – дифференциальным законом распределения СВ.
Свойства функции распределения случайной величины.
1)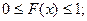
2) F(x) – неубывающая;
3) F(-∞)=0, F(+∞)=1;
4) P(x1<X<x2)=F(x2)-F(x1);
5)F(x) непрерывна слева.
Свойства функции плотности вероятности.
1)f(x) ≥0(как производная неубывающей функции);
2) P(x1<X<x2)=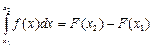 ;
;
3)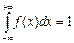 (площадь, заключенная под всей кривой, изображающей плотность распределения, равна 1);
(площадь, заключенная под всей кривой, изображающей плотность распределения, равна 1);
4)f(+∞)=f(-∞)=0.
Числовые характеристики НСВ.
2) Медиана находится из условия . Решив данное уравнение, необходимо проверить принадлежность полученного решения соответствующему промежутку. 3) . Математическое ожидание НСВ сохраняет все свойства математического… 4) . Дисперсия НСВ сохраняет все свойства дисперсии ДСВ.Законы распределения НСВ.