Вільні осі. Головні осі інерції. Моменти інерції різних тіл

При обертанні тіла навколо довільно обраної осі в загальному випад-ку вісь обертання або повертається, або переміщується відносно умовно не-рухомої системи відліку. Для того, щоб така вісь обертання залишалася в незмінному положенні, до неї необхідно прикласти певні зовнішні сили.

При обертанні однорідного симетричного тіла вісь обертання збері-гала б своє положення в просторі без впливу на неї ззовні. Вісь обертання тіла, положення якої в просторі зберігається без дії на неї будь-яких сил ззовні, називають вільною віссю тіла.

Для тіла будь-якої форми і з будь-яким розподілом маси існує три вза-ємно перпендикулярні осі, що проходять через центр інерції тіла, які мо-жуть служити вільними осями – їх називають головними осями інерції. У загальному випадку головні осі інерції тіла можуть бути обрані не в будь-якому довільному напрямку, а лише в певному, тобто вони фіксовані. В од-норідного тіла із площинною симетрією (наприклад, паралелепіпеда) фіксо-вані дві головні осі інерції. В однорідного тіла з осьовою симетрією (напри-клад, циліндра) фіксована лише одна з головних осей інерції (вісь цилінд-ра). В однорідного тіла із центральною симетрією (кулі) жодна з головних осей інерції не фіксована.

Моменти інерції відносно головних осей називають головними мо-ментами інерції тіла 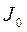. У загальному випадку ці моменти різні:

Для тіла з осьовою симетрією два головні моменти інерції мають однакову величину, а третій відмінний від них: 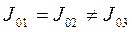. Для тіла із цен-тральною симетрією всі три головні моменти інерції однакові:

Момент інерції тіла описується рівнянням (7.26). Масу речовини Δm_i можна виразити через густину речовини ρ і об'єм . Густина речовини в будь-якій точці виражається співвідношенням:

(7.31)

Тут вираз ΔV→0 означає, що об'єм стягується до тієї точки тіла, де визначається густина ρ, але ΔV≠0, а обмежується деяким мінімальним об'ємом, у межах якого можна говорити про густину речовини. Таким чи-ном, враховуючи (7.31), величину моменту інерції можна виразити рів-нянням:

(7.32)

Сума (7.32) тим точніша, чим менші ΔV_i. Отже, завдання знаходження мо-ментів інерції зводиться до обчислення інтеграла виду:

(7.33)

Для однорідних за густиною тіл

Розглянемо кілька окремих прикладів роз-рахунку моментів інерції однорідних симетричних тіл.

7.6.1. Момент інерції циліндра. Відносно головної осі інерції ОО (рис.7.8) момент інерції

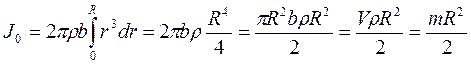
Рис.7.8 Для визначення моменту інерції відносно осі

z' скористаємося теоремою Штейнера: момент інерції 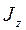відносно довіль-ної осі z, паралельної головній осі інерції, дорівнює сумі головного моменту інерції 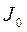й добутку маси тіла т на квадрат відстані 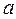між осями:

(7.34)

З доведенням теореми Штейнера можна ознайомитись у посібнику [1].

Вісь z' відстоїть від осі ОО на відстані . Тоді момент інерції циліндра відносно осі z' дорівнює:

.

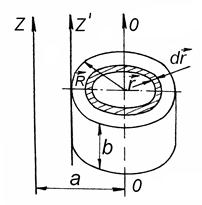
7.6.2. Момент інерції товстостінного циліндра з порожниною відносно головної осі інерції.

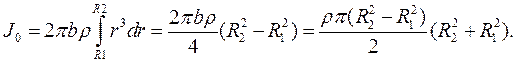
Тут R₁ й R₂ – внутрішній і зовнішній радіуси циліндра відповідно:

– об’єм пустотілого циліндра.

Тоді:

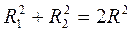7.6.3. Головний момент інерції тонкостінного циліндра. Для тонкостінного циліндра можна прийняти, що і , і

7.6.4. Момент інерції матеріальної точки m відносно довільної осі обертання z, що відстоїть на відстані 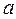від точки згідно з рівняннями (7.27) і (7.34) дорівнює: .

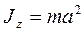7.6.5. Момент інерції тонкого довго-го стержня з постійним перетином S будь-якої форми. Елемент об'єму dV стержня при обертанні його навколо головної осі інерції ОО (рис. 7.9) дорівнює . Тоді

 

Рис.7.9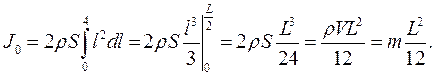

Тут L – довжина стержня. Згідно з теоремою Штейнера момент інерції стержня відносно осі z дорівнює:

 

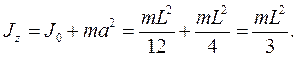
7.6.6. Момент інерції тонкого диска відносно осі, що співпадає з діаметром диска. Елементарний момент інерції

(рис.7.10). За умови, що товщина диска , момент інерції диска від-носно осі Z знайдемо за рівнянням:

 

7.6.7. Головний момент інерції кулі. Для однорідної кулі . Елементарний момент інерції (рис. 7.11). Згідно з теоремою Піфагора 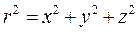. Сферична система симетрична, і середні значення

Рис. 7.10 Рис. 7.11

 

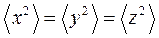. Прийнявши, що , знаходимо:

.

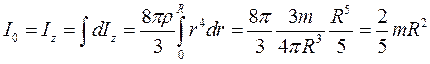І для диска, і для кулі – маса однорідного тіла, ρ – густина речовини.

 

7.7. Тензор інерції

 

Розглянемо обертальний рух тіла відносно закріпленої точки О, котра співпадає з початком інерціальної системи відліку (рис 7.12).

Проведемо через точку О миттєву вісь ОА. Нехай 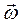– миттєва кутова швидкість тіла відносно ціеї осі. Момент імпульсу частинки 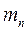цього тіла відносно точки О:

Рис.7.12.

Момент імпульсу всього тіла

Всі частинки тіла мають одну й ту саму кутову швидкість 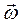. Тому рівняння моменту імпульсу можна записати в проекціях на осі координат, наприклад:

Оскільки то

Подібні рівняння можна записати для 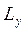та . Останнє рівняння має три коефіцієнти:

.

Кожен із цих коефіцієнтів залежить від миттєвої орієнтації тіла від-носно осей координат . Їх називають інерціальними коефіцієнтами або моментами інерції:

(7.35)

Аналогічно можна записати коефіцієнти для проекцій 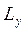та . Врахо-вуючи всі коефіцієнти та рівняння, отримуємо систему рівнянь для всіх компонентів моменту імпульсу:

 

(7.36)

Сукупність дев’яти величин

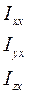
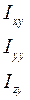
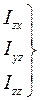(7.37)

називають тензором інерції тіла відносно точки О, а самі ці величини – компонентами цього тензора, або компонентами матриці (див. [4] та [5]).Сукупність рівнянь (7.36) вказує на те, що у випадках тіл довільної форми з довільним розподілом маси момент імпульсу не є простим добутком скаляра 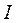на вектор 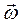кутової швидкості. Тому взагалі напрямок вектора не співпадає з напрямком вектора .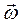

Величини називають діагональними компонентами тензора, а всі інші – недіагональними. Вони симетричні: . Діагональні компоненти, наприклад є сумою добутків кожної маси на квадрат її відстані від осі обертання, тому їх називають моментами інерції відносно осі.

Якщо – густина тіла в точці, радіус-вектор якої є , то кожен мо-мент інерції можна записати у вигляді інтегралів, наприклад:

.

Очевидно, що сума діагональних компонентів

(7.38)

На підставі рівняння (7.38) обчислимо головний момент інерції однорідної кулі радіуса , мас якої :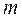

що співпадає з результатами (7.6.7).