Вимоги до моделей

 

У загальному випадку під час побудови моделі потрібно враховувати такі вимоги:

- незалежність результатів розв'язання задач від конкретної фізичної інтерпретації елементів моделі;

- змістовність, тобто здатність моделі відображати істотні риси і властивості реального процесу, який вивчається і моделюється;

- дедуктивність, тобто можливість конструктивного використання моделі для отримання результату;

- індуктивність - вивчення причин і наслідків, від окремого до загального, з метою накопичення необхідних знань.

1.6 Комп'ютерне та імітаційне моделювання

 

Комп'ютерне моделювання визначимо як реалізацію моделі за допомогою комп'ютера. Особливістю комп'ютерного моделювання є його інтерактивність, що дає змогу користувачу втручатися в процес моделювання та впливати на результати завдяки узгодженості дій користувача і моделі, яка відтворює об'єкти реального середовища або гіпотетичні події та процеси. Під час комп'ютерного моделювання може бути задіяно реальні об'єкти (наприклад, кабіна пілота), віртуальні об'єкти, згенеровані комп'ютером, які відтворюють реальні об'єкти (наприклад, потоково-конвеєрна лінія для збирання автомобілів). Інтерактивне комп'ютерне моделювання широко застосовується в навчальних системах, наприклад для побудови тренажерів і в ситуаційних іграх.

Що стосується математичних моделей, або математичного моделювання, то слід відзначити, що під час їх використання багато чого залежить від способу подання як моделі, так і результатів моделювання. Розглянемо простий приклад. Нехай на деякому підприємстві для водопостачання використовується резервуар, об'єм якого становить W тисяч літрів. Рівень споживання — V_n тисяч літрів, а швидкість наповнення резервуара — V₃ тисяч літрів за добу. Необхідно знайти час Г, за який буде заповнено резервуар. Схему цієї системи зображено на рисунку 1.2, де резервуар позначено прямокутником, а вхідний і вихідний потоки — стрілками з «вентилями», які регулюють ці потоки. Хмарки позначають необмежені потоки. Такі ідеограми широко використовуються під час побудови моделей неперервних процесів.

Знайдемо час заповнення резервуара

 

Рисунок 1.2 – Схема системи водопостачання

 

(1.1)

 

Ця математична модель процесу наповнення резервуара є надто ідеалізованою, тому що всі її параметри вважаються незмінними в часі, зовнішні впливи на систему не враховуються. Завдяки такій ідеалізації маємо дуже просту модель, яка дає змогу розв'язати задачу аналітично. Однак за допомогою такої моделі можна отримати відповідь тільки на одне конкретне запитання — за який час буде заповнено резервуар.

Якщо задачу наблизити до практики, то, будуючи модель, необхідно враховувати, що потреби підприємства у водопостачанні постійно змінюються, більш того, можливі перебої в роботі насосів під час подавання води. Розв'язок задачі в частково замкнутому вигляді можна записати як:

 

(1.2)

За рахунок неявного запису отримано більш придатну для дослідження та аналізу реальних процесів математичну модель. Час заповнення резервуара об'ємом W залежить від параметрів моделі V₃, V_n.

Використання вивчити відношення між величинами V_п, і V₃, якщо задавати різні початкові значення для них, і побудувати графік наповнення резервуара (рис.1.3).

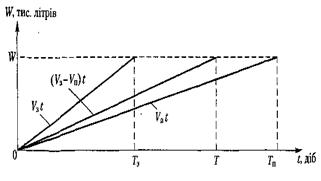
Рисунок 1.3 – Графік наповнення резервуара

 

Реалізувати цю модель можна за допомогою і чисельних методів. Змінюючи у формулі (1.2) значення t від 0 з деяким кроком Δί до такого, що буде виконуватись рівність (1.4), отримаємо динамічну характеристику заповнення резервуара. Чим менший крок Δί, тим точніший отримаємо результат, але тим довше буде вирішуватись задача моделювання.

Термін «моделювання» відповідає англійському слову «modeling», тобто побудові моделі та її аналізу. Англійський термін «simulation» відповідає прийнятому терміну «імітаційне моделювання», але часто вони використовуються разом, коли йдеться про технологічні або системні етапи моделювання, пов'язані з прийняттям рішень за допомогою моделей.

Імітаційне моделювання — це метод конструювання моделі системи та проведення експериментів. Однак під таке визначення підпадають майже всі види моделювання. Тому потрібно виділити суттєві особливості імітаційного моделювання.

Перш за все слід подати в моделі структуру системи, тобто загальний опис елементів і зв'язків між ними, потім визначити засоби відтворення в моделі поведінки системи. Здебільшого поведінку системи описують за допомогою станів і моментів переходів між ними. Стан системи в момент часу t визначають як безліч значень певних параметрів системи у цей самий момент часу t. Будь-яку зміну цих значень можна розглядати як перехід до іншого стану. І врешті-решт, імітаційна модель має відобразити властивості середовища, в якому функціонує досліджувана система. Зовнішнє середовище задають вхідними впливами на модель.

Вся інформація про імітаційну модель загалом має логіко-математичний характер і подається у вигляді сукупності алгоритмів, які описують процес функціонування системи. Отже, здебільшого імітаційною моделлю є її програмна реалізація на комп'ютері, а імітаційне моделювання зводиться до проведення експериментів з моделлю шляхом багаторазового прогону програми з деякою множиною даних — середовищем системи. Під час імітаційного моделювання може бути задіяно не тільки програмні засоби, але й технічні засоби, люди та реальні системи.

З математичної точки зору імітаційну модель можна розглядати як сукупність рівнянь, які розв'язують з використанням чисельних методів у разі кожної зміни модельного часу. Окремі рівняння можуть бути простими, але їх кількість і частота розв'язання — дуже великими. Розв'язання таких рівнянь під час імітаційного моделювання означає встановлення хронологічної послідовності подій, які виникають у системі і відображають послідовність її станів. Отже, імітаційна модель функціонує так само, як система.

Якщо повернутись до процесу наповнення резервуара (рис.1.4), то за допомогою імітаційної моделі весь процес можна відтворити з використанням рівняння (1.2). Позначимо через W_і поточний стан резервуара, який відтворюється в певні моменти модельного часу, що змінюється з постійним кроком Δt.

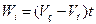, (1.3)

де t_i = t_i_₁ + Δt (і = 1, 2,...), t₀ = 0.

Така модель є детермінованою. Процес моделювання закінчується, якщо на деякому кроці виконується умова W < W_i,, тобто розв'язок отримуємо за один прогін імітаційної моделі. Точність результату буде залежати від значення Δί.

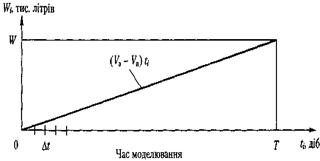
Рисунок 1.4 – Динамічна характеристика наповнення резервуара

Зa наявності в моделі випадкових факторів виникає необхідність статистичного оцінювання результатів моделювання, що виконується за допомогою методу статистичного моделювання (методу Монте-Карло). Статистичне моделювання є самостійним видом моделювання, яке включається в імітаційне моделювання тільки за необхідності моделювання ймовірнісних систем і процесів.

Побудуємо більш реальну модель системи, яка розглядалась вище. Припустимо, що рівень споживання води на підприємстві має імовірнісний характер і змінюється згідно з рівномірним розподілом імовірності в межах V_п ± ΔV_п. Тоді значення V_n у деякий момент часу t_i будемо визначати як

,

 

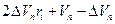де r_i - випадкове число, рівномірно розподілене в інтервалі [0, Δ]. В результаті роботи імітаційної моделі після кожного прогону, отримаємо випадкові значення Т_j, де j — кількість прогонів, j = 1, 2, 3, .... Для кожного прогону потрібно задавати свою послідовність випадкових чисел r_i. Отримані значення Т_j будуть відрізнятись від середнього значення Т, знайденого за допомогою детермінованої моделі. Таким чином, щоб оцінити час Τ наповнення резервуара, потрібно задати точність оцінювання ε = ΔT і рівень довіри α. Звичайно α = 0,95, тобто є гарантія, що в 95 випадках із 100 середнє значення часу Τ буде знаходитись у межах Τ ± ΔT.

Із вищенаведеного прикладу видно, що стохастичне моделювання використовується під час імітаційного моделювання тільки за необхідності врахування випадкових факторів.

 

2 ПОБУДОВА ІМІТАЦІЙНИХ МОДЕЛЕЙ

2.1 Основні принципи побудови математичних моделей

Вихідною інформацією при побудові математичних моделей є дані про призначення і умови функціювання системи, що досліджується або проектується. Така інформація визначає мету моделювання системи 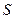і допомагає сформулювати основні вимоги до моделі. Степінь абстрагування (спрощення) залежить від характеру задач, які стоять перед проектантом системи.

При моделюванні складних систем важливо подати її у вигляді певного моделюючого алгоритму (графічного образу), який полегшує створення математичної моделі і дає можливість всю систему розглядати як сукупність простіших елементів, які взаємодіють між собою і навколишнім середовищем.

Моделюючий алгоритм (математичну схему) можна визначити як проміжну ланку при переході від словесного до формального опису функціювання системи з врахуванням дії навколишнього середовища.

Кожна конкретна система (елемент системи) 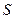характеризується сукупністю властивостей, під якими розуміють величини, що відтворюють поведінку реальної системи і враховують умови її функціювання при взаємодії із зовнішнім середовищем .

Модель системи відтворює у вигляді математичних співвідношень взаємозв’язок між певними величинами, які враховують як дію зовнішнього середовища, так і умови функціювання самої системи. Множина таких величин утворює наступні підмножини: сукупність вхідних дій на систему

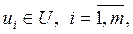(2.1)

де під вхідними діями розуміють певні фізичні величини, за допомогою яких можна змінити стан системи;

сукупність дій зовнішнього середовища

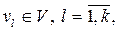(2.2)

сукупність внутрішніх (власних) параметрів системи

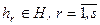(2.3)

сукупність вихідних характеристик великої системи

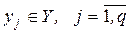(2.4)

В загальному випадку , , 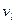і є елементами підмножин, що не перетинаються, і можуть бути як стохастичними, так і детермінованими величинами.

При моделюванні системи 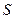вхідні дії, дії зовнішнього середовища і внутрішні параметри системи є незалежними (екзогенними) величинами, які відповідно можна подати у векторній формі :

Вихідні характеристики (величини) системи (2.4) є залежними (ендогенними) змінними і також можуть бути подані у векторній формі .

Процес функціонування системи в загальному випадку характеризується оператором , який перетворює вхідні величини у вихідні, у відповідності із співвідношенням

. (2.5)

Залежність (2.5) називається законом функціювання системи 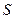і позначається символом . В загальному випадку закон функціювання системи може бути поданий у вигляді функції, функціоналу, логічних умов в алгоритмічній і табличній форах або у вигляді словесного правила відповідності.

Іншим важливим поняттям, яке необхідне для опису системи 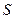є алгоритм функціювання 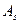, під яким розуміють метод отримання вихідних характеристик системи 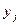з врахуванням вхідних дій, дій зовнішнього середовища і власних параметрів системи. Один і той же закон функціювання системи може породжувати сукупність алгоритмів функціювання .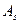

Співвідношення (2.5) в загальному випадку характеризує поведінку системи в часі , тобто відтворює його динамічні властивості. Тому математичні моделі такого типу носять назву динамічних моделей системи.

В тому випадку, коли вихідні характеристики системи залишаються постійними, то співвідношення (2.5) задає статичну модель об’єкта

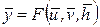(2.6)

Для характеристики стану системи часом буває недостатньо мати лише вихідні величини y_j. Найповніше стан системи описується за допомогою змінних 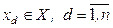. Тоді стан системи 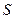можна характеризувати вектором 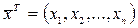, який для різних моментів часу приймає певні значення.

Якщо процес функціювання системи розглядати як послідовну зміну її станів 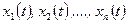, то останні можна інтер-претувати як координати в 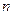-вимірному евклідовому просторі. А сам простір носить назву фазового простору, тобто фазовий простір утворений всіма можливими станами системи .

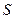Стан системи в момент часу повністю визначається початковими умовами , вхідними діями 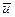, діями зовнішнього середовища 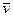і внутрішніми параметрами 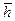за допомогою двох векторних рівнянь

, (2.7)

 

. (2.8)

Рівняння (2.7) за початковим станом 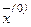і екзогенними змінними 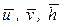визначає вектор-функцію 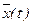, а друге за отриманим значенням 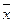– ендогенні змінні системи .

Таким чином, послідовність рівнянь “вхід-стан-вихід” дає можливість визначити вихідні характеристики системи

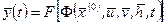(2.9)

Якщо математичний опис системи не вміщує величини , або її вплив на функціювання системи нехтується, то модель системи носить назву детермінованої. Очевидно, що детермінована модель є частковим випадком стохастичної моделі.

Можна зробити висновок, що при дослідженні процесу функціювання системи в неперервному часі, коли не враховуються випадкові величини , використовують детерміновані моделі, які можуть бути у вигляді диференціальних, інтегральних, інтегродиферен-ціальних, алгебраїчних та інших рівнянь, а для опису систем, які функціонують в дискретному часі – кінцеві автомати і кінцево-різницеві схеми.

Використання стохастичних моделей для опису систем з дискретним часом приводить до ймовірносних автоматів, а для подання систем з неперервним часом – систем масового обслуговування.

Таким чином, побудова математичних моделей процесів функціювання систем опирається на такі основні принципи:

- неперервно-детермінований (диференціальні рівняння);

-дискретно-детермінований (кінцеві автомати, різницеві схеми);

- неперервно-стохастичний (системи масового обслуговування);

-дискретно-стохастичний (ймовірності автомати);

- узагальнений або універсальний (агрегатні системи).

Узагальнений принцип побудови математичних моделей дає можливість створити агрегатні моделі (схеми) шляхом розбиття складної системи на окремі елементи (підсистеми) із збереженням зв’язків між ними. Агрегатні моделі відносяться до найбільш універсальних і дають можливість описувати складні системи на основі системного підходу.

2.2 Неперервно-детерміновані моделі (D-моделі)

Неперервно-детерміновані моделі від-творюють динаміку (англ. Dynamic) процесу функціювання системи у формі диференціальних рівнянь, які можуть бути звичайними або в часткових похідних. Малі моделі скорочено називають D-моделями.

Процес створення D-моделей в своїй основі має певні фізичні закони, які визначають функціювання системи 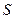. На основі таких законів записують математичні співвідношення, які зв’язують між собою екзогенні і ендогенні змінні.

Як приклад, розглянемо методику створення D-моделі механічної системи, яка складається із масивного тіла, пружини і демпфера (рис. 2.1).

 

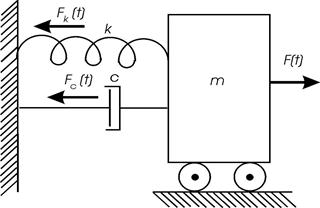
Рисунок 2.1 – Механічна система

На рисунку 2.1 k-коефіцієнт жорсткості пружини, H/м;

С – затухання, 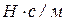; m – маса, кг.

Допустимо, що вхідна дія системи – прикладене зусилля 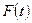, а вихідною характеристикою системи є її зміщення в напрямку координації осі .

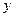Основним фізичним законом, який лежить в основі функціювання механічної системи є закон збереження кількості руху, який подамо в диференціальній формі

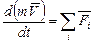, (2.10)

де – швидкість (векторна величина);

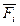– сили, які діють на систему

Нехтуємо впливом зовнішнього середовища на систему, яке проявляється через тертя і опір повітря.

Оскільки m = const, а вектори швидкості і зусиль колінеарні, то рівняння (2.10) можна замінити скалярним

,

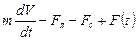де 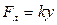– сила натягу пружини;

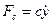– сила демпфірування;

– швидкість.

Отже, рівняння руху системи матиме такий вигляд

. (2.11)

Рівняння (2.11) перепишемо в дещо іншій формі

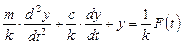. (2.12)

Введемо такі позначення .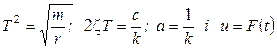

Тоді рівняння (2.12) буде таким:

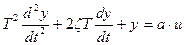, (2.13)

де .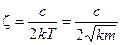

Безрозмірна величина в формулі (2.13) носить назву коефіцієнта затухання системи. Якщо її значення лежить в межах 0<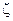<1, то в системі виникають згасаючі коливання.

Розглянемо інший приклад, коли системою є електричне коло, яке складається із активного опору , ємності 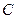і індуктивності 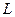(рис. 2.2). До входу електричної системи прикладена напруга U₁, а вихідною характеристикою системи є напруга U₂ на виході еклектичного кола.

 

У відповідності з теорією електричних кіл

U₁=U_L+U_R+U₂, (2.14)

 

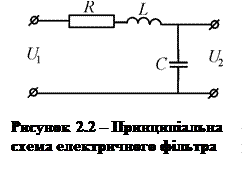
де U_L – напруга на індуктивності; U_R – напруга на опорі;

Для того щоб отримати математичну модель системи необхідно із рівняння (2.14) вилучити проміжні змінні U_L і U_R.. Відомо, що

,

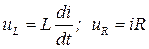де і – струм в електричному колі.

З інших сторони струм і протікає через ємність С і тому має місце співвідношення

.

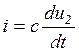Тому .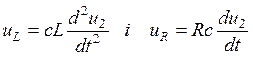

Отже,

.

Введемо такі позначення :

.

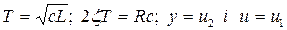Тоді

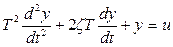. (2.15)

Як і в механічній системі при 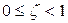в електричній системі виникають згасаючі коливання.

Аналіз математичних моделей (2.14) і (2.15), які описують системи різної фізичної природи, показує, що вони мають однакові структури, різниця лише в значеннях внутрішніх параметрів систем. В цьому і проявляється принцип аналогії, коли різні системи, в яких протікають різні фізичні можуть мати однакові за структурою математичні моделі. Це означає, що процеси функціювання одних систем можуть бути вивчені через поведінку інших систем з відмінною від перших фізичною природою. Наприклад, закон руху механічної системи можна вивчити, спостерігаючи зміну напруги на виході електричної системи, за умови, що величини у і 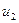певним чином відмасштабовані.

 

2.3 Основні форми подання математичних моделей

 

В залежності від конкретної задачі, яку розв’язує дослідник, математичну модель об’єкта необхідно подати в тій чи іншій формі. Всі ці форми є еквівалентними, вони відтворюють одні і ті ж динамічні властивості об’єкта. Тому необхідно вміти переходити від однієї форми до іншої.

У практиці керування лінеризовані математичні моделі подаються у формі диференціальних рівнянь, передавальних функцій, в формі системи диференціальних рівнянь (в просторі станів), в матрично-векторній формі і в формі матричних передавальних функцій.

Форма диференціальних рівнянь. Якщо у-вхід об’єкта, а 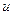- його вихід, то взаємозв’язок між 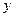і 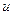в динаміці можна відтворити диференціальним рівнянням 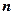-го порядку з постійними коефіцієнтами

, (2,16)

де 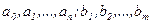- постійні коефіцієнти.

Інколи користуються іншою індексацією постійних коефіцієнтів, коли індекс коефіцієнта співпадає з порядком похідної, тобто

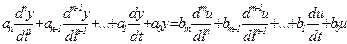
Для реальних об’єктів завжди має місце співвідношення 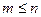, яке носить назву умови фізичної реалізації системи.

Форма передавальної функції . Рівняння (7.31) і (7.32) відтворюють динамічні властивості об’єкта (системи) в часовій області, а передавальна функція дає можливість описати динаміку об’єкта в частотній області. Ця форма математичної моделі ґрунтується на перетворенні Лапласа .

Подання математичної моделі в просторі станів. Для розв’язку цілого ряду задач - моделювання на цифрових ЕОМ, оптимізації, “аналітичного” конструювання регуляторів та інше - застосовують опис об’єктів у просторі станів.

Такий опис виникає природнім шляхом при моделюванні багатовимірних об’єктів або в результаті заміни диференціального рівняння 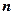- го порядку системою диференціальних рівнянь. Таку заміну можна здійснити декількома способами.

Перший спосіб. Цей спосіб можна застосувати в тому випадку, коли права частина диференціального рівняння не вміщує похідних. В такому випадку маємо

.

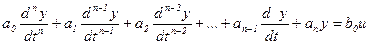Розв’яжемо диференціальне рівняння (2.16) відносно старшої похідної

.

Введемо змінні стану об’єкта

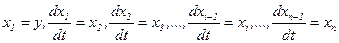
Тоді .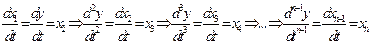

Таким чином, маємо таку систему диференціальних рівнянь

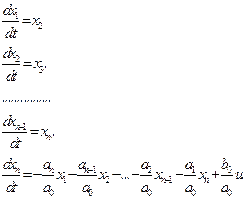(2.17)

Якщо скористатись оператором суми, то останнє рівняння системи (2.17) можна подати в компактнішому вигляді

,

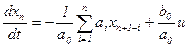Третій спосіб. Розглянемо диференціальне рівняння (2.16) в якому . Якщо це не так, то, прирівнюючи до нуля коефіцієнти 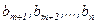, завжди зможемо записати диференціальне рівняння у вигляді

.

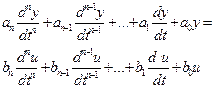Рівняння розпадається на систему диференціальних рівнянь першого порядку

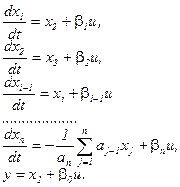(2.18)

Величини визначаються як розв’язок системи лінійних алгебраїчних рівнянь

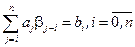. (2.19)

Цей спосіб найуніверсальніший, оскільки він не накладає ніяких обмежень на порядок похідної в правій частині диференціального рівняння (2.79)

Приклад 1. Математичну модель об’єкта 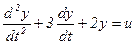подати в просторі станів, використовуючи перший і другий способи .

Перший спосіб. Оскільки порядок диференціального рівняння 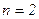, то динамічні параметри об’єкта в просторі станів будуть характеризуватись двома диференціальними рівняннями першого порядку .

Використовуючи рівняння (2.17) при 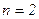, отримаємо :

Оскільки 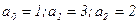і , то

 

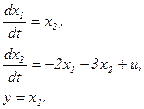
Приклад 2. Математичну модель об’єкта 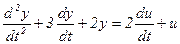подати в просторі станів, використавши третій спосіб . Оскільки 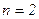, то у відповідності з (2.18)

В нашому випадку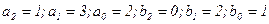

Невідомі величини 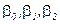знайдемо із системи рівнянь (2.19). Для 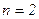одержуємо

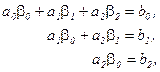
З врахуванням числових значень відповідних коефіцієнтів маємо систему рівнянь

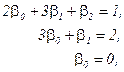
із якої визначаємо -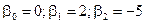

Отже,

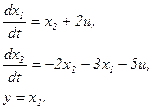
3 ІМОВІРНІСНЕ МОДЕЛЮВАННЯ