Генератори випадкових чисел

Найбільше прикладів генерування випадкових чисел можна знайти в ігровому бізнесі. Це номери в спортивних лотереях, числа, які випадають на рулетці, варіанти розкладу карт тощо. Більшість комп'ютерних ігор теж базується на випадкових числах.

Типи генераторів.Без комп'ютера використання випадкових чисел, передбачене методом статистичних випробувань, не має сенсу, тому генератори випадкових чисел повинні бути безпосередньо з'єднані з комп'ютером. Це можна зробити за допомогою апаратних приставок до комп'ютера (апаратні методи) або спеціальних програм (програмні методи). Крім того, під час моделювання можна використати готові таблиці випадкових чисел, які слід розміщати в пам'яті комп'ютера або на зовнішньому накопичувачі.

Апаратні методи генерування випадкових чисел базуються на використанні деяких фізичних явищ (наприклад, шумів електронних приладів, радіоактивного випромінення та ін.). Під час застосування апаратних генераторів випадковий електричний сигнал перетворюють у двійковий код, який вводиться в комп'ютер за допомогою спеціальних аналого-цифрових перетворювачів. Один з найбільш поширених методів — це використання шумів електронних приладів. Якщо на підсилювач не подавати ніякого сигналу та увімкнути його на повну потужність, то буде чутно шипіння (шум). Це і є шум електронних елементів підсилювача, який є випадковим процесом. Цей неперервний сигнал можна перетворити в дискретний. Існують різні схеми перетворення випадкового сигналу в послідовність двійкових цифр. У більшості випадків його підсилюють і встановлюють граничне значення напруги шумового сигналу, перевищення якого можна вважати значенням двійкової одиниці на деякому малому проміжку часу t. У протилежному випадку отримуємо двійковий нуль. Для отримання m-розрядного випадкового двійкового числа провадиться т вимірювань неперервного сигналу у фіксовані моменти часу t₁ t₂, ..., t_m.

Вбудовані в комп'ютери апаратні генератори випадкових чисел останнім часом часто використовуються в системах захисту інформації. Прикладом застосування таких генераторів для забезпечення конфіденційності, цілісності та достовірності електронної інформації, яка зберігається в комп'ютері або передається по мережі, є пристрій для шифрування даних PadLock, інтегрований у деякі моделі процесорів, розроблених компанією Intel. Пристрій має інтерфейс прикладного рівня, що дає змогу розробникам програмного забезпечення отримувати випадкові числа без використання програмних драйверів. Такий спосіб отримання високоякісних випадкових послідовностей простіший та ефективніший, ніж використання апаратно-програмної RNG (Random Number Generator) архітектури і суто програмних генераторів, що особливо важливо під час побудови захищених програм.

Табличний метод. У 1955 році корпорація «Ренд» опублікувала таблиці випадкових чисел, які мали мільйон значень. Для заповнення цих таблиць застосовувались апаратні методи. Дані цих таблиць можна використовувати під час моделювання систем за допомогою методу статистичних випробувань. У сучасних комп'ютерах ці таблиці можна зберігати на зовнішніх носіях або навіть в основній пам'яті. Головним недоліком табличного методу є те, що під час його використання витрачаються значні об'єми основної пам'яті комп'ютера.

Найбільш розповсюдженими на практиці є програмні генератори, які дають змогу отримувати послідовності випадкових чисел за рекурентними формулами. Якщо бути абсолютно точним, то числа, які виробляють програмні генератори, насправді є псевдовипадковими («псевдо» у перекладі з грецької — нібито). Так їх називають тому, що алгоритми їх отримання завжди є детермінованими.

Загалом же програмні генератори повинні задовольняти таким вимогам:

- генерувати статистично незалежні випадкові числа, рівномірно розподілені в інтервалі [0, 1];

- мати можливість відтворювати задані послідовності випадкових чисел;

- затрати ресурсів процесора на роботу генератора повинні бути мінімальними;

- легко створювати незалежні послідовності випадкових чисел (потоки).

Слід звернути увагу на те, що більшість програмних генераторів виробляють випадкові числа, рівномірно розподілені в інтервалі [0, 1]. Необхідність моделювання таких чисел обумовлена тим, що на їх основі можна отримати випадкові числа практично будь-яких розподілів.

Якість роботи генераторів визначається статистичними властивостями послідовностей випадкових чисел, які він виробляє, — незалежністю і випадковістю. Властивості послідовностей перевіряються за статистичними критеріями, детально описаними нижче.

Здатність відтворювання послідовності випадкових чисел полягає в тому, що за однакових початкових умов і параметрів генератор повинен відтворювати одні й ті ж послідовності псевдовипадкових чисел. Ідентичні послідовності випадкових чисел рекомендується використовувати у випадку, коли потрібно порівняти альтернативні варіанти систем, що моделюються, і налагодити програми. Однак можливість відтворення не завжди бажана під час моделювання систем і в комп'ютерних іграх (як це було в перших версіях відомої гри «Тетріс», коли кожна гра починалась з тієї ж послідовності). Для усунення недоліку – початкові значення величин брати з таймера комп’ютера.

Під час дослідження складних систем виникає необхідність у моделюванні послідовностей випадкових чисел великої довжини. Для їх створення потрібні швидкодіючі алгоритми генерування з мінімальними вимогами до ресурсів комп’ютера.

У більшості генераторів використовується рекурентна процедура 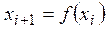. Найпростішим та найдавнішим серед таких генераторів є генератор фон Неймана та Метрополіса, робота якого базувалась на методі середини квадратів. Суть його.

Зобразимо довільне чотирирозрядне десяткове число як х х х х. Піднесемо його до квадрату і в отриманому результаті відкинемо по дві цифри зліва і справа.

 

х х х х

х х х х

х х |х х х х | х х

 

Чотири цифри, які залишилися і є новим числом. Якщо результат множення менше цифр ніж 8, то зліва дописують нулі.

Недоліки:

- якщо початковечисло парне, то може відбутись виродження послідовності, тобто з деякого всі=0;

- числа, які виробляє генератор, є сильно корельовані.

Лінійні конгруентні генератори

У більшості сучасних програмних генераторів використовується властивість конгруентності, яка полягає в тому, що два цілих числа А і В є конгруентними за модулем т, якщо їх різниця (А-В) є числом, яке ділиться на т без остачі ( тобто є кратним т).

Записується це так:

А=В( mod m).

Наприклад, щоб знайти число, конгруентне з числом 134 за моделем 10, необхідно знайти цілочислову остачу від ділення 134 на 10, яка = 4

Наведемо кілька прикладів обчислення конгруентних значень для різних т:

12 = 5 (mod 7); 35 = 5 (mod 10); 125 = 5 (mod 10).

Серед методів генерування випадкових чисел найбільш поширеним є ліній­ний мультиплікативний конгруентний метод:

х_і+1 = (ах_і + с) mod т, (3.1)

де і = 1, 2,...; а, с і т - цілі константи.

Щоб отримати нове число, необхідно взяти псевдовипадкове число х, (або задати вихідне х₀), помножити його на коефіцієнт а, додати константу с і взяти модуль отриманого числа за т, тобто розділити на т, і отримати остачу. Ця остача і буде наступним псевдовипадковим числом х_і+1. У разі правильного підбору параметрів цей генератор повертає випадкові числа від 0 до т-1.

Отримані за формулою (3.1) значення x_i+i належать до діапазону 0 < х_і+х < т - 1 і мають рівномірний дискретний розподіл. Для того щоб отримати випадкове значення г_і+1 з інтервалу [0, 1], необхідно число х_і+1 розділити на т. У цьому разі всі значення т, с, a, x₀ повинні бути додатними й задовольняти умовам: 0 < т; а < т; с < т; х₀< т. Отримана за формулою (3.1) послідовність називається лінійною конгруентною послідовністю.

Однією із вад лінійних конгруентних генераторів є те, що отримані випадкові числа X_і+1суттєво залежать від значень т, с, а, х_о і обчислюються за однією й тією ж формулою (3.1), тобто не є абсолютно випадковими. Але незважаючи на те що алгоритм їх отримання є детермінованим, за умови відповідного вибору констант т, с, а послідовність чисел х_і+1, на основі яких отримують значення г_і+1, повністю задовольнятиме більшості статистичних критеріїв.

Ще одна вада цих генераторів стосується того, що випадкові числа г_і+1, отримані за допомогою генератора, можуть приймати тільки дробово-раціональні значення — 0; І/т; 2/т;...; (т- 1)/т. Більше того, числа r_і+1 можуть приймати лише деякі з указаних значень залежно від вибраних параметрів т, с, а і х_о, а також від того, як реалізується операція ділення чисел з плаваючою комою на число от у комп'ютері, тобто залежно від типу комп'ютера і системи програмування. Наприклад, якщо т = 10, х_о = а = с = 7, то отримаємо послідовність 7; 6; 9; 0; 7; 6; 9; 0,..., яка не є випадковою. Це свідчить про важливість правильного вибору значень констант от, с, а і х₀. Правильно підібрані значення іноді називають магічними числами.

Наведений приклад ілюструє й те, що конгруентна послідовність завжди є циклічною, тобто вона починає повторюватися через певну кількість випадкових чисел. Кількість значень, після яких випадкові числа починають повторюватися, називається повним періодом генератора і є основним його параметром. Значення повного періоду залежать від розрядності комп'ютера, а також від значень т, с, а і х₀ . Існує теорема, яка визначає умови існування повного періоду генератора, а саме:

- числа с і т повинні бути взаємно простими, тобто мати взаємний дільник 1;

- значення b= а - 1 має бути кратним q для кожного простого q, бути дільником т;

- значення b має бути кратним 4, якщо m кратне 4.

Достатність цих умов уперше було доведено Халлом (Hull) і Добеллом (Dobell).

Якщо с > 0, то генератор називається мішаним, а якщо с = 0 — мультиплікативним.

Розглянемо, як потрібно вибирати параметри лінійного конгруентного генератора, щоб отримати послідовність з повним періодом. Для отримання такої послідовності необхідно вибирати значення т = 2^g - 1, де g - довжина розрядної сітки комп'ютера. Для 32-розрядного комп'ютера т — найбільше ціле число, яке може бути відтворене в ньому, дане число дорівнює 2³¹ - 1 = 2147483647 (один розряд відводиться під знак числа). У цьому разі ділення X_i+1/m виконувати не обов'язково. Якщо в результаті роботи генератора буде отримане число х_і+1, яке більше ніж те, що може бути відтворене в комп'ютері, виникне переповнення розрядної сітки. Це призведе до втрати крайніх лівих двійкових знаків цілого числа, які перевищили допустимий розмір. Однак розряди, що залишились, саме і є значеннями х_І+1 (mod 2^g). Таким чином, під час генерування замість операції ділення можна скористатись переповненням розрядної сітки.

Стосовно константи с теорема стверджує, що для отримання послідовності з повним періодом генератора значення с повинне бути непарним, і, крім того, а- 1 має ділитися на 4. Для такого генератора початкове значення х₀ може бути довільним і лежати в діапазоні від 0 до т - 1. Якщо с = 0, то отримуємо мультиплікативний конгруентний метод, який передбачає використання таких рекурентних виразів:

x_i= аx_i (mod m). (3.2)

Цей метод більш швидкодіючий, ніж попередній, але він не дає послідовності з повним періодом. Дійсно, з виразу (3.2) видно, що значення х_і+1 = 0 може з'явитись тільки в тому випадку, якщо послідовність вироджується в нуль. Взагалі, якщо d — будь-який дільник m i x_i кратне d, всі наступні елементи мультиплікативної послідовності х_і+1, х_і+2,... будуть кратними d. Таким чином, якщо с = 0, потрібно, щоб x_i і т були взаємно простими числами з т і знаходились між 0 і т.

Що стосується вибору а, то у випадку, коли m = 2^g, де g >= 4 значення а=:

а = 3 (mod 8) або а = 5 (mod 8).

У цьому випадку четверта частина всіх можливих значень множників дає довжину періоду, що дорівнює т/4, яка й буде максимальним періодом генератора.

3.3 Статистичні критерії

Наша основна мета отримати послідовність, яка веде себе так, якби вона була випадковою. Вище розповідалось, як зробити період послідовності настільки довгим, що при практичному застосуванні він ніколи не буде повторюватись. Це важливий критерій, але він не дає гарантій, що послідовність буде використовуватись в додатках. Як вирішити, чи достатньо випадковою буде послідовність.

Якщо дати навгад вибраній людині папір і олівець і попросити його написати 100 десяткових цифр, то дуже мало шансів, що буде отриманий позитивний результат. Люди стараються уникати дій, які приводять до результатів, що здаються не випадковими, такими як наприклад, поява пари рівних суміжних цифр (хоч приблизно 1 з 10 цифр повинна рівнятись попередній). І якщо показати тій же людині таблицю справжніх випадкових чисел, вона, напевно, скаже, що ці числа невипадкові. Вона запримітить багато закономірностей.

У відповідності з висловами доктора І.Дж.Матрікса, який цитував Мартіна Гарднера в Scientific American, January, 1965, “Математики розглядають десятинне розкладання числа π як випадкову послідовність, але сучасний спеціаліст з магічних властивостей чисел знайде для себе багато цікавих прикладів”. Матрікс вказав, наприклад, що першим двозначним числом, що повторюється в розміщенні числа π є 26, а другий раз воно повториться якраз посередині повторених пар чисел.

Склавши список багатьох подібних властивостей цих чисел він запримітив, що розкладання числа π, якщо його правильно інтерпретувати, може розказати про всю історію людства.

Всі ми помічаємо закономірності в наших телефонних номерах, номерах водійських прав та ін., щоб їх запам’ятати. Наша основна думка є в тому, що неможна бути упевненим в тому, що дана послідовність є випадковою. Для цього потрібно застосувати якийсь критерій.

Теоретична статистика надає деякі кількісні міри випадковості. Існує буквально велика кількість критеріїв які можна використовувати для перевірки того чи буде послідовність випадковою. Обговоримо критерії з нашої точки зору, найбільш корисні, найбільш повчальні і найбільш пристосовані до вирахування на комп’ютерах.

Якщо критерії Т₁Т₂, …..Т_n підтверджують що послідовність веде себе випадково, це ще не означає, що перевірка з допомогою Т_n+1 - го критерію буде успішною. Проте кожна успішна перевірка дає все більше і більше впевненості у випадковості послідовності. Зазвичай до послідовності застосовується біля пів дюжини статистичних критеріїв і якщо вони задовольняють ці критерії, то послідовність рахується випадковою (це презумпція невинності до доказу вини)

Кожну послідовність, яка буде широко застосовуватись необхідно ретельно перевірити. В наступних розділах пояснюється як правильно застосовувати критерії. Розрізняють два види критеріїв: емпіричні критерії, при використанні яких комп’ютер маніпулює групами чисел послідовності і вираховує певні статистики, і теоретичні критерії, для яких характеристики послідовності визначаються з допомогою теоретично-числових методів, основаних на рекурентних правилах, які використовують для утворення послідовності.

 

3.4 Основні критерії перевірки випадкових спостережень А. критерій “хі-квадрат”

Критерій “хі-квадрат” (х²-критерій), можливо найвідоміший з усіх статистичних критеріїв. Він є основним методом, що використовується в поєднанні з іншими критеріями. Перш ніж розглядати ідею в цілому, проаналізуємо приклад застосування х²-критерію до кидання гральних кубиків. Використаємо два “правильні” гральні кубики (кожен з яких незалежно допускає випадіння значень 1,2,3,4,5 або 6 з рівною імовірністю.) В наступній таблиці дана ймовірність отримання певної суми s при одному киданні гральних кубиків.

Значення 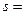2 3 4 5 6 7 8 9 10 11 12

Ймовірність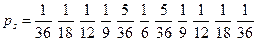

Наприклад, величина 4 може бути отримана трьома способами: 1+3,2+2,3+1; це складає 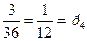із 36 можливих результатів.

Якщо кидати гральний кубик n разів, то в середньому ми отримаємо величину s приблизно np_s разів. Наприклад, при 144 киданнях величина 4 випадає біля 12 разів. В наступній таблиці показано, які результати справді отримані при 144 киданнях гральних кубиків.

Значення 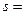2 3 4 5 6 7 8 9 10 11 12

Спостережуване число,

Y_s = 2 4 10 12 22 29 21 15 14 9 6

Очікуване число, np_s = 4 8 12 16 20 24 20 16 12 8 4

Відмітимо, що у всіх випадках спостережуване число відрізняється від очікуваного числа. Справді, результати випадкового кидання гральних кубиків навряд чи завжди будуть появлятись саме з правильною частотою. Існує 36¹⁴⁴ можливих послідовностей 144 кидань, і всі вони рівно можливі. Одна з таких послідовностей складається із всіх двійок (“зміїне око”), і кожен хто викинув 144 зміїні ока підряд, буде впевнений, що кубики обтяжені. Незважаючи на це послідовність усіх двійок є такою ж ймовірною, як і будь яка друга послідовність, якщо точно визначити результат кожного кидання кожного кубика.

В наведеному вище прикладі цілком природно розглянути квадрати різностей між спостережуваними числами Y_s і очікуваними числами np_s. Можна скласти їх, отримавши

(3.3)

Поганий набір гральних кубиків привів би до відносно великого значення V, а для даного значення V можна сказати наступне: “Чому рівна ймовірність таких великих значень V, якщо використовувати “правильні” гральні кубики?” Якщо ця ймовірність дуже мала, наприклад 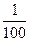, ми будемо знати що тільки біля одного разу із ста “правильні” гральні кубики,будуть давати результати настільки віддалені від очікуваних значень, що виникають певні підстави для підозри (Пам’ятаємо, що ті ж самі хороші гральні кубики будуть давати таке велике значення V приблизно в одному випадку із ста, так що передбачуваним особам прийдеться повторювати експеримент, коли більші значення V є частковими)

В статистиці V в (3.3) доданках 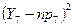і 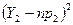приписується рівна вага незважаючи на те що 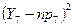напевно буде більше ніж 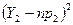, так як 7 появляється приблизно в 7 разів частіше ніж 2. Виявляється що “правильна” статистика по крайній мірі статистика яка як доказано найбільш важлива, буде приписувати 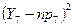тільк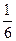и ваги 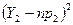, і необхідно змінити (3.3) наступним чином:

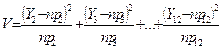(3.4)

Ця статистика називається статистикою “хі-квадрат” спостережуваних значень Y₂ ,… Y₁₂ при киданні гральних кубиків. Для даних із таблиці (2) отримуємо, що

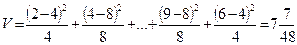
Тепер виникає важливе запитання: “Чи буде 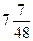незвичайно великим значенням для V при наших припущеннях?” Перш ніж відповісти на нього, розглянемо як застосовується метод “хі-квадрат” в загальних ситуаціях. Припустимо, що кожне спостереження може належати до одної із k категорій. Проводимо n незалежних спостережень. Це означає що результат одного спостереження абсолютно не впливає на результат іншого спостереження. Нехай p_s – ймовірність того, що кожне спостереження відноситься до категорії s і нехай Y_s – число спостережень, яке дійсно відноситься до категорії s. Створимо статистику:

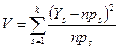(3.5)

В прикладі, що наведений вище, існує 11 можливих результатів кожного кидання гральних кубиків, тобто k=11

Зводячи в квадрат 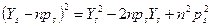в (6) і враховуючи той факт, що

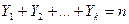(3.6)

 

 

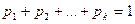
отримуємо формулу:

 

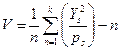(3.7)

яка значно спрощує вирахування V.

Повернемось до запитання: “Чому рівне прийняте значення V?” Його можна визначити з допомогою таких таблиць, як таблиця 1, яка дає значення “х²-розподілу з υ ступенями свободи” для різних значень υ. Використовуємо рядки таблиці з υ=k-1 так як число ступенів свободи дорівнює k-1, що на одиницю менше, ніж число категорій. Тому треба рахувати, що число ступенів свободи дорівнює k-1. Ці аргументи не є строгими, але вони підтверджуються теоретично. Якщо в таблиці вибрати число х, що стоїть на υ-рядку і в стовпчику p, то “ймовірність того, що значення V в (3.7) буде менше або рівне х, приблизно рівне р, якщо n достатньо велике”.

	p=1%	p=5%	p=25%	p=50%	p=75%	p=95%	p=99%
υ=1	0.0002	0.00393	0.1015	0.455	1.323	3.841	6.635
υ=2	0.0201	0.1026	0.5754	1.386	2.773	5.991	9.210
υ=3	0.1148	0.3518	1.213	2.366	4.108	7.815	11.34
υ=4	0.2971	0.7107	1.923	3.357	5.385	9.488	13.28
υ=5	0.5543	1.1455	2.675	4.351	6.626	11.07	15.09
υ=6	0.8721	1.635	3.455	5.348	7.841	12.59	16.81
υ=7	1.239	2.167	4.255	6.346	9.037	14.07	18.48
υ=8	1.646	2.733	5.071	7.344	10.22	15.51	20.09
υ=9	2.088	3.325	5.899	8.343	11.39	16.92	21.67
υ=10	2.558	3.940	6.737	9.342	12.55	18.31	23.21
υ=11	3.053	4.575	7.584	10.34	13.70	19.68	24.72
υ=12	3.571	5.226	8.438	11.34	14.85	21.03	26.22
υ=15	5.229	7.261	11.04	14.34	18.25	25.00	30.58
υ=20	8.260	10.85	15.45	19.34	23.83	31.41	37.57
υ=30	14.95	18.49	24.48	29.34	34.80	43.77	50.89
υ=50	29.71	34.76	42.94	49.33	56.33	67.50	76.15

В певній мірі добре, що для використання таблиць немає значення, чому рівні n і ймовірність p_s. Тільки число υ=k-1 впливає на результат. Треба відмітити, що значення таблиці 1 це тільки наближені значення: справа в тому, що в ній наведені значення х²-розподілу, які є граничним розподілом випадкової величини V формулі (3.5). Тому табличні значення наближені до реальних тільки при великих n. Наскільки великими повинні бути n? Емпіричне правило говорить: треба взяти n настільки великим, щоб всі значення величини 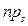були більші або рівні 5. Проте краще брати набагато більше n, щоб отримати надійний критерій. В приведеному вище прикладі n=144, np₂ дорівнювало тільки 4 і емпіричне правило було порушене.

Питання про правильний вибір n достатньо складне. Якщо гральні кубики дійсно не симетричні, то це буде проявлятись все більше і більше при зростанні n. Але при великих значеннях n має місце тенденція до згладжування локальної невипадкової поведінки, коли блоки чисел із строгим зміщенням ідуть за блоками чисел з протилежним зміщенням. При реальному киданні гральних кубиків згладжування локальної невипадкової поведінки можна не боятися так як одні і ті ж гральні кубики використовуються під час всього експерименту, але випадковість ймовірних чисел, що генеруються комп’ютером може досить часто демонструвати такі аномалії. Можливо x²-критерій потрібно було б застосовувати для кількох різних значень n. У будь якому випадку, значення n повинно було бути по можливості великим.

4 МОДЕЛЮВАННЯ ВИПАДКОВИХ ПОДІЙТА ДИСКРЕТНИХ ВЕЛИЧИН

 

У разі дослідження складних систем методом статистичних випробувань необхідно мати можливість отримувати за допомогою комп'ютера вибіркові значення випадкових величин, які мають різні закони розподілу. Випадкові величини зазвичай моделюють за допомогою перетворення одного або кількох незалежних значень випадкової величини R, рівномірно розподіленої в інтервалі [0, 1], що позначаються як r_i„ і =1, 2, 3,... (r_i є [0,1]). Значення r_i генерують, як звичайно, за допомо­гою програмних генераторів випадкових чисел.

4.1 Незалежні випадкові події

Припустимо, що ймовірність настання деякої елементарної випадкової події А в одному випробуванні дорівнює Р(A) = р. Вважається, що умови проведення кожного випробування однакові і його можна повторити нескінченну кількість разів. Якщо r_i - це значення рівномірно розподіленої в інтервалі [0, 1] величини, то можна стверджувати, що за умови r_i < ρ (рис. 4.4) настане подія А, а якщо r_i > р, то відбудеться подія А.

Рисунок 4.1 – Моделювання настання випадкових подій

 

Ця модель добре описує такі події, як обслуговування вимоги в пристрої СМО, що може бути вільним або зайнятим, успішну або ні спробу виконання деякого завдання, влучення або ні в ціль, розгалуження потоків інформації у двох і більше напрямках. У деяких мовах для моделювання випадкової події використовується спеціальний блок (наприклад, у мові GPSS — блок TRANSFER, який працює в статистичному режимі ).

4.2 Група несумісних подій

Нехай є група несумісних подій А1, А2,..., Ак, настання яких необхідно дослідити. Відомі ймовірності настання цих подій р1=Р(А1), ...рк=Р(Ак). Якщо події несумісні, то 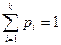. Припустимо, що р0=0. На відрізку [0,1] числової осі відкладемо значенняцих імовірностей.

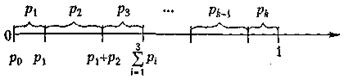
Рисунок 4.2 - Моделювання групи несумісних подій

Якщо отримане від генератора випадкових чисел значення г_і потрапляє в інтервал від 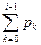до 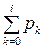вважаємо, що відбулася подія А_і. Таку процедуру називають визначенням результату випробування за жеребом. Вона грунтується на формулі

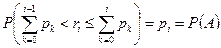(4.1)

де р₀ = 0.

Ця модель часто використовується в теорії прийняття рішень і добре відтворює процеси вибору однієї з багатьох альтернатив у комп'ютерних іграх, розгалужен­ня потоків інформації у вузлах мережі в кількох напрямках, вибір одного з бага­тьох пристроїв для обслуговування в СМО і т. ін.

4.3 Умовна подія

Умовна подія А - це подія, яка відбувається з імовірністю Ρ (А/В) тільки за умо­ви, що настала подія В (рис. 3.5). У цьому разі має бути задана ймовірність Р(B) настання події В. Моделювання настання умовної події А провадиться таким чи­ном. Спочатку випадкове число r₁ отримане від генератора випадкових чисел, використовується для моделювання настання події В. Подія В настає в тому випад­ку, якщо справджується нерівність r₁ < Ρ (В). Настання події А моделюється за допомогою числа r₂. Для цього перевіряється умова r₂ < Р(А), за виконання якої приймається рішення, що подія А відбулася. Якщо ж подія В не відбулася (тобто настає подія В), то настання події А моделювати не потрібно. Таким чином, мож­на скоротити загальну кількість випробувань

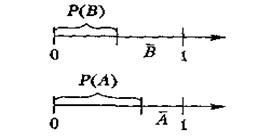
Рисунок 4.3 – Моделювання настання

умовної події