Количественные меры риска

 

 

В процессе принятия решения в ситуациях, связанных с риском,

 

удобней пользоваться не качественными мерами риска, а количественными,

 

как более легко интерпретируемыми и объективными. В связи с этим

 

направления количественной оценки риска имеют достаточно давнюю

 

историю. В настоящее время разработано большое число количественных

 

подходов к оценке риска. Исчерпывающий их перечень составить не

 

представляется возможным, но к наиболее распространенным методам

 

количественной оценки риска относятся:

 

· срок до исполнения обязательств;

 

· меры вариации (изменчивости):

 

 

o от среднего значения (дисперсия, среднее квадратическое

 

отклонение, коэффициент вариации);

 

o от линии тренда;

 

o отклонение от среднего только в одну сторону

 

(полудисперсия, стандартное полуотклонение,

 

полувариация);

 

· волатильность;

 

· Value-at-Risk;

 

· риск разорения;

 

· коэффициент риска;

 

· коэффициент Кука;

 

· вероятность возникновения потерь;

 

· модели ценообразования активов;

 

· стресс-тестирование;

 

· анализ чувствительности;

 

· сценарный анализ;

 

· имитационное моделирование по методу Монте-Карло;

 

· «греческие» меры риска для производных финансовых

 

инструментов, и другие

 

Модели ценообразования активов будут подробнее рассмотрены в

 

главе 4; «греческие» меры риска – в главе 5; показатели вариации

 

относительно линии тренда и полувариация, а также стресс-тестирование – в

 

главе 6; анализ чувствительности, сценарный анализ и имитационное

 

моделирование – в главе 7.

 

Оценим основные преимущества и недостатки отдельных

 

количественных методов оценки риска, используемых в большинстве для

 

оценки финансовых рисков, однако применимых и для других

 

разновидностей экономических рисков.

 

45

 

Одной из простейших количественных мер риска является срок до

 

исполнения обязательств. Если рассмотреть эту меру на примере

 

финансовых инструментов, то это будет – срок, оставшийся до погашения

 

финансового инструмента. Очевидно, что при прочих равных условиях

 

инструмент с большим сроком имеет и больший риск, если все другие

 

факторы риска не принимать во внимание.

 

Рассмотрим инструмент с фиксированным поступлением доходов

 

(например, облигацию). Для, оценки риска рассчитывают средний срок

 

поступления, который обобщает сроки поступления денег от инструмента

 

(без учета процентных платежей) в виде средневзвешенной арифметической

 

величины16:

 

 

∑ tS

n

 

 

t

∑ S

TA =

t=1

n

 

 

t

t=1

 

где Та – средний срок поступлений;

 

St – суммы поступлений (без купонного дохода);

n – общий срок инструмента;

 

t – сроки платежей.

 

Такой показатель легок в расчете и в интерпретации. Однако для

 

инвестора огромную роль играет временная ценность денег. В этой связи в

 

качестве весов можно использовать не сами денежные суммы, а их

 

дисконтированные значения. Показатель, учитывающий временную

 

стоимость денег, называют эквивалентный срок:

 

 

∑ tS v

n

 

 

t

 

t

∑ S v

Te =

t=1

n

 

t=1

 

 

t

 

t

 

 

Четыркин Е.М. Финансовые риски. – М.: Издательство «Дело»,2008.

 

46

 

где Stvt – дисконтированные суммы поступлений;

vt – дисконтирующий множитель по ставке i за срок t, vt=(1+i)-t.

 

Очевидно, что при положительной процентной ставке (i>0)

 

эквивалентный срок будет меньше, чем средний срок поступлений, причем

 

чем больше будет значение ставки, тем больше будет разность Та–Тe. В

финансах эти меры, рассчитанные для различных ценных бумаг (прежде

 

всего облигаций), называют дюрациями17.

 

Другой простейшей количественной мерой риска может быть

 

изменчивость цены (или, например, доходности) интересующего нас актива –

 

ведь именно неблагоприятные колебания цен приносят убытки владельцу

 

актива. В статистике существует множество мер, которые позволяют

 

измерить изменчивость (вариацию) значений экономического показателя.

 

Однако наибольшее распространение получило стандартное отклонение:

 

∑ (x

n

 

 

t

 

− x)2

ó =

t=1

 

n

 

где x – среднее значение случайной переменной xt;

n – количество наблюдений.

 

В качестве случайной переменной xt можно рассматривать изменение

цены актива за определенный период (чаще всего за один день). Чтобы не

 

привязываться к абсолютным показателям рассчитываются относительные

 

изменения цен, выраженные в долях или процентах:

 

xt =

 

pt − pt−1

pt−1

 

100%

 

 

где pt – цена актива в момент времени t.

 

 

17 Наиболее полно рассмотрено применение дюраций для целей управления риском в Энциклопедии

финансового риск-менеджмента/Под ред. Лобанова А.А. и Чугунова А.В. – М.: Альпина Бизнес Букс, 2007г.

 

ln=tx

%100

47

 

Если мы рассматриваем непрерывную ставку наращения, то случайную

 

переменную xt можно рассчитать следующим образом:

 

 

 pt 

 pt−1 

 

В ряде книг этот показатель риска называют волатильность. Однако у

 

термина волатильность есть и более широкое толкование – изменчивость

 

какого-либо экономического показателя. В практике анализа инструментов

 

финансового рынка под волатильностью понимают неустойчивость цен

 

финансового актива на рынке (или их неустойчивость относительно линии

 

тренда). Таким образом, волатильность характеризует именно случайную

 

составляющую изменения цены – плановое (прогнозируемое) изменение

 

цены не несет в себе риска для инвестора.

 

Так как волатильность является случайной величиной, то ее

 

действительно удобно характеризовать с помощью стандартного отклонения,

 

но это не единственный возможный показатель. Поэтому нельзя считать эти

 

показатели синонимами.

 

На практике волатильность может определяться не только путем

 

расчетов непосредственно по статистике цен актива, но и исходя из моделей

 

ценообразования финансовых инструментов, которые будут рассмотрены в

 

главе 4.

 

При рассмотрении изменения цены за несколько интервалов времени

 

мы получаем временной ряд. Моделирование данной случайной величины

 

представляет основу для оценки большинства рыночных рисков. Ниже

 

приводятся основные способы моделирования волатильности18:

 

· простая волатильность;

 

· экспоненциальная волатильность;

 

 

18 Жердер В. М. Методы оценки финансового риска. Методические указания по изучению курса/Рост. гос.

экон. ун-т. – Ростов н/Д, 2005.

 

48

 

· ARCH/GARCH модели;

 

· прогнозируемая (implied) волатильность;

 

· реализованная (realized) волатильность.

 

В рамках простейшего представления волатильность рассматривается

 

как нормально распределённая случайная величина с дисперсией, равной

 

дисперсии изменения цены за интервал. В качестве оценки волатильности

 

используется стандартное отклонение данной величины, рассчитанное по

 

некоторой исторической выборке. Если для расчета используется выборка

 

небольшого объема, то необходимо применять выборочное стандартное

 

отклонение:

 

∑ (x

n

 

 

t

 

− x)2

ó выб =

t=1

 

n − 1

 

На практике, в большинстве случаев инвестор располагает выборками

 

достаточно большого объема (например, для расчета однодневной

 

волатильности желательно использовать данные не менее чем за 60 торговых

 

дней) и в результате различия между стандартным отклонением и

 

выборочным стандартным отклонением несущественны. В дальнейшем, для

 

простоты изложения, мы не будем делать различия между ó и ó выб .

 

Достоинством этой модели является ее простота. Чтобы оценить с

 

заданной надежностью максимально возможное отклонение цены от

 

среднего ожидаемого значения, достаточно просто умножить волатильность

 

на коэффициент, определяемый свойствами нормального распределения. Так

 

методика RiskMetrics рекомендует 95% надежностью и соответственно

 

коэффициент 1,65. Базельский комитет рекомендует коэффициент 2,33, что

 

соответствует 99% надежности.

 

49

 

Однако эта модель имеет ряд недостатков19:

 

· Несоответствие нормального распределения реальному

 

распределению случайных движений цен. Реальные случайные

 

движения цен в целом не так сильно отклоняются относительно нуля,

 

как это задает нормальное распределение, но совершают иногда резкие

 

скачки (имеют т.н. «тяжелые хвосты»). Представленные нормальным

 

распределением случайные изменения, с одной стороны, склонны к

 

сравнительно большим колебаниям около нуля, но, с другой стороны

 

не склонны к резким выбросам. Последнее наиболее неприятно, т.к.

 

именно резкие случайные движения цен представляют наибольший

 

интерес при оценке потерь.

 

· Расчёт характеристик волатильности по значительному

 

историческому массиву приводит к «запаздыванию» оценки –

 

произошедшие в течение последних дней или недель изменения

 

волатильности не найдут в полной мере свое отражение в ее оценке. С

 

другой стороны, при регулярном (например, ежедневном) расчете

 

волатильности с одной и той же длиной выборки выход из выборки

 

резких скачков, имевших место в прошлом, будет приводить к резкому

 

изменению текущей волатильности.

 

· Данный подход не учитывает возможную автокорреляцию

 

случайных изменений цен – например, в случае резкого однодневного

 

скачка цен в последующие дни случайные изменения цен будут также

 

выше своей «средней нормы», что способно существенно повлиять на

 

характер принимаемых рисков.

 

Экспоненциальная волатильность представляет собой аналог простой

 

волатильности с единственным отличием – при расчете стандартного

 

отклонения данные исторической выборки включаются в расчёт с весовыми

 

 

Жердер В. М. Методы оценки финансового риска. Методические указания по изучению курса/Рост. гос.

экон. ун-т. – Ростов н/Д, 2005.

 

50

 

коэффициентами, увеличивающими вес недавних движений цен в выборке

 

по сравнению с давними движениями.

 

Простые представления о волатильности исходят из того, что

 

случайные изменения цен на каждом временном интервале не зависят друг от

 

друга. Реальное поведение случайных изменений обычно не соответствует

 

данному допущению. Для волатильности характерна, т.н. «кластеризация»,

 

т.е. периоды, когда абсолютные значения волатильности принимают

 

большие или меньшие значения20.

 

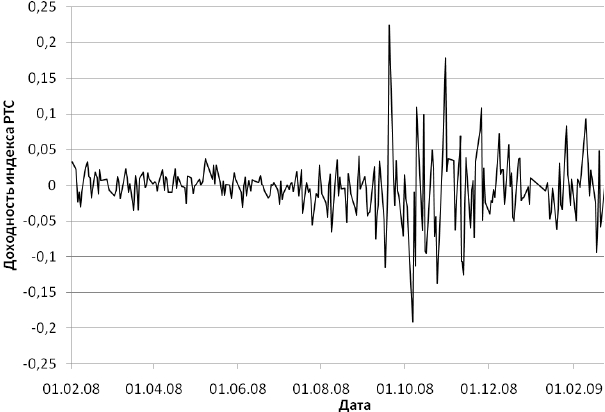
Рис. 3.1. График доходности инвестиций в индекс РТС

 

 

Например, если проанализировать динамику доходности индекса РТС

 

(рассмотрение доходностей нагляднее характеризует движения индекса) с

 

февраля 2008 по март 2009 года (рис. 3.1), можно выделить два основных

 

периода. В начале года колебания индекса были незначительны. Вторая часть

 

 

Жердер В. М. Методы оценки финансового риска. Методические указания по изучению курса/Рост. гос.

экон. ун-т. – Ростов н/Д, 2005.

 

 

графика соответствует периоду, когда мировая экономика вошла в кризис. В

 

это время индекс РТС, среагировав на определённые новости, совершал

 

значительные скачки, причем за резкими выбросами следовали затухающие

 

колебания. Если для такого рынка произвести оценку возможных потерь от

 

инвестиций в фондовый индекс (или акции, входящей в индекс), не учитывая

 

серийность случайных движений цен, то оценка риска может оказаться

 

заниженной или завышенной, в зависимости от периода оценки.

 

Для учета серий случайных больших колебаний доходностей

 

финансовых инструментов при расчете волатильности используют

 

ARCH/GARCH-модели. ARCH-модель моделирует стандартное отклонение

 

доходности в виде суммы константной базовой волатильности и линейной

 

функции абсолютных значений нескольких последних изменений цен. При

 

этом уровень волатильности рассчитывается по рекурсивной формуле.

 

Расширением ARCH-модели является GARCH-модель волатильности,

 

где на текущую волатильность влияют как предыдущие изменения цен, так и

 

предыдущие оценки волатильности (т.н. «старые новости»).

 

На основе понятия волатильности строится множество и других мер

 

риска. Например, в современном риск-менеджменте огромной

 

популярностью пользуется показатель VAlUe-At-Risk (VAR), в буквальном

 

переводе означающий «стоимость под риском».

 

Дело в том, что для многих инвесторов стандартное отклонение

 

требует дополнительной интерпретации – неясен возможный размер потерь.

 

В отличие от стандартного отклонения VaR – это оценка величины, которую

 

не превысят ожидаемые потери в течение определенного периода с заданной

 

вероятностью. Причем VaR сразу выражается в денежных единицах.

 

Показатель VaR может рассчитываться как для отдельного актива, так

 

и для портфеля. Как правило, VaR не используется для оценки риска на

 

рынках, находящихся в состоянии кризиса.

 

Математически VaR можно представить следующим образом:

 

P(VAR ≥ x) = 1 − á ,

 

52

 

где х – это потери (случайная величина),

 

1-α – заданная доверительная вероятность.

 

Рис. 3.1 иллюстрирует положение VaR на графике плотности

 

распределения вероятности доходности инструмента (портфеля) для

 

доверительной вероятности (1-α).

 

Плотность распределения

 

α

 

Доходность

 

 

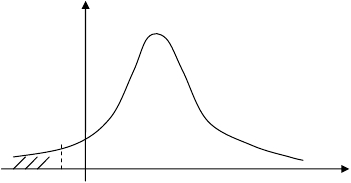
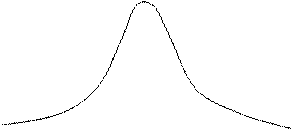
Рис. 3.2. Определение величины VaR на графике распределения доходностей

 

 

На рисунке 3.2 заштрихована область наиболее неблагоприятных

 

(стрессовых) ситуаций, вероятность которых составляет α%, соответственно

 

доверительная вероятность составит в этом случае (1-α)%. Тогда VaR – это

 

значение доходности, слева от которого сосредоточено α% распределения.

 

Оценка VAR зависит от:

 

· временного горизонта, который выбирается исходя из срока

 

удержания инструмента или его ликвидности. Например, рассчитывают

 

«однодневный VaR», «недельный VaR» «месячный VaR». Базельский

 

комитет рекомендует банкам временной горизонт в 10 дней;

 

· уровня доверия. Например, Базельский комитет рекомендует

 

банкам уровень в 99%, а на практике чаще используется 95% уровень;

 

· предположений о законе распределения доходностей

 

инструмента. Наиболее часто делается предположение о нормальном законе

 

распределения.

 

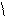
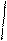
53

 

Рассмотрим наиболее распространенный дельта-нормальный метод,

 

предложенный инвестиционным банком J.P. Morgan в системе RiskMetrics.

 

Размер прибыли или потерь по инструменту за день будет равняться

 

его изменению цены за этот день. Поэтому наименьшая ожидаемая цена с

 

вероятностью (1-α) равна:

 

 

Pt+1 = Pt exp(µt − k1−áó t )

 

где µt – математическое ожидание однодневной доходности инструмента,

 

зачастую на практике принимается равным нулю;

 

k1−á – перцентиль уровня α распределения доходностей инструмента;

 

ó t

 

– стандартное отклонение однодневных доходностей, может

 

рассчитываться как на основе обычной выборочной дисперсии, так и на

 

основе моделей, например экспоненциального сглаживания, ARCH, GARCH

 

и их модификаций.

 

Тогда оценка величины VaR будет равна наибольшему ожидаемому

 

изменению цены за один день:

 

 

VAR = Pt (exp(µt − k1−áó t ) − 1)

 

Величину exp(µt − k1−áó t ) − 1 можно заменить на ее приближенное

 

значение

 

µt − k1−áó t . При расчете VaR для временного горизонта,

 

превышающего один день, однодневное стандартное отклонение

 

масштабируют. Тогда в общем случае для временного горизонта Т дней

 

 

T 

ô 



VAR = V  µt



 

T

ô

 

− k1−áó t

 



 

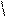
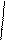
54

 

где V – текущая стоимость позиции (Pt умножить на количество единиц

инструмента);

 

µt

 

и ó t – математическое ожидание и стандартное отклонение

 

доходности инструмента за τ дней.

 

Такой показатель называют абсолютным VaR. В случае, если есть

 

проблемы в определении ожидаемой доходности, рассчитывают

 

относительный VaR. Он определяется как величина потерь относительно

 

произвольной ожидаемой доходности:

 

VARrel = Vk1−áó t

 

T

ô

 

В практике управления финансовыми рисками используется множество

 

других количественных мер риска – однако рассмотренные выше меры

 

являются наиболее популярными. Отдельный раздел финансового риск-

 

менеджмента посвящен оценке риска производных финансовых

 

инструментов.

 

Кроме этих мер риска, оценивающих риск владения каким-либо

 

активом, рассчитывают и ряд других показателей. Например, часто возникает

 

необходимость оценить риск разорения. Пусть собственный капитал фирмы

 

(или инвестора) ограничен величиной C. Тогда если размер убытков Y,

 

превысит собственный капитал С, это приведет к разорению. Под риском

 

разорения r понимают вероятность наступления убытков, превышающих

 

величину С:

 

 

r = P(Y > C)

 

При расчете этого показателя, как правило, возникает проблема оценки

 

вероятности. Чтобы оценить эту вероятность, возможные убытки Y

 

раскладывают на составные части. Например, убыток Y может складываться

 

55

 

из убытков по владению ценными бумагами, убытков из-за невозврата

 

кредитов, падения спроса на производимый продукт и т.п. После этого

 

разложения оценивается вероятность возникновения убытков по каждой из

 

составляющих. Когда все же невозможно оценить вероятность,

 

рассчитывают коэффициент риска:

 

K1 =

 

 

Y

C

 

 

По сути, этот коэффициент характеризует нашу возможность покрыть

 

максимально возможные потери за счет собственного капитала. При

 

принятии решения коэффициент риска можно ограничить некоторым

 

пороговым значением î1.

Если же существует возможность оценить вероятность потерь p, то

 

рассчитывают взвешенный коэффициент риска:

 

K2 =

 

 

pY

C

 

 

Взвешенный коэффициент риска в свою очередь можно ограничить

 

некоторым пороговым значением î 2. Также можно рассчитать обратные

коэффициенты, называемые коэффициентами покрытия риска:

 

K покр. р =

 

 

C

Y

 

и

 

K взвеш.покр. р. =

 

 

C

pY

 

В банковской сфере аналогом этих коэффициентов является

 

коэффициент Кука:

 

H K =

 

 

Собственные средства

Активы взвешенные с учетом риска

 

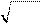
56

 

Для банковской сферы часто оценивается депозитный риск – риск

 

досрочного отзыва депозита. Массовый отток депозитов может привести к

 

серьезным последствиям для банка. Оценить вероятность депозитного риска

 

можно с помощью формулы Бернулли:

 

 

P( X = k ) = Cnk pk q n−k

 

где Cn =

k

 

n!

k!(n − k )!

 

 

,

 

X – количество отзываемых вкладов (случайная величина);

 

n – общее число депозитов;

 

k – число от 0 до n;

 

p – вероятность отзыва одного отдельного депозита, а q=1-p.

 

Тогда вероятность того, что будут отозваны не менее k депозитов,

 

можно найти так:

 

P(X ≥k) = P(X=k) + P(X=k+1) + … +P(X=n).

 

 

При больших значениях n можно использовать формулы Пуассона или

 

Муавра-Лапласа:

 

P( X = k ) ≈

 

ë k

k !

 

e−ë

 

 

где ë = n,

 

 

 â − np   á − np 

P(á < X < â ) ≈ Ö0   −Ö0  

 npq   npq 

 

57

 

где Ф0 – функция Лапласа,

 

 

ϕ0  

P( X = k ) ≈

 

1  k − np 

npq  npq 

 

где ϕ0 – плотность распределения нормального закона.

 

Если обозначить через X не количество отзываемых вкладов, а

 

количество дефолтов по выданным кредитам, то вместо депозитного риска

 

по этим же формулам мы можем оценить вероятность кредитного дефолта.

 

Эта методика называется CreditRisk+ и позволяет оценить риск дефолта без

 

учета его причин.

 

58