рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Образование
- /
- А) Непосредственное моделирование.
Реферат Курсовая Конспект
А) Непосредственное моделирование.
А) Непосредственное моделирование. - раздел Образование, СТАТИСТИЧЕСКОЕ МОДЕЛИРОВАНИЕ Если ...
Если 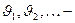 последовательность независимых случайных величин с распределением Бернулли, то есть
последовательность независимых случайных величин с распределением Бернулли, то есть 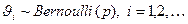 , тогда случайная величина
, тогда случайная величина 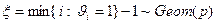 , где
, где 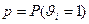
Алгоритм генерирования 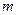 значений случайной величины
значений случайной величины 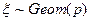 :
:
1. Задаем  и
и  .
.
2. Генерируют значение случайной величины 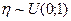 :
: 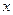 .
.
3. Если 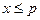 , то
, то  . В противном случае
. В противном случае 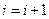 .
.
4. Если 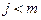 возвращаемся к шагу 2. В противном случае переход к шагу 5.
возвращаемся к шагу 2. В противном случае переход к шагу 5.
5. Полученная последовательность 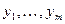 является выборкой объема
является выборкой объема 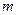 значений случайной величины имеющей геометрическое распределение.
значений случайной величины имеющей геометрическое распределение.
б) Моделирование с помощью показательного распределения.Пусть  , тогда
, тогда
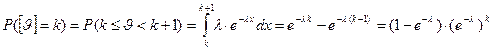
и следовательно, случайная величина 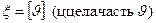 имеет геометрическое распределение с параметром
имеет геометрическое распределение с параметром 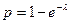 . Поэтому если взять
. Поэтому если взять 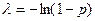 , то
, то  будет иметь нужное нам распределение. Следовательно, если
будет иметь нужное нам распределение. Следовательно, если 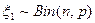 и
и 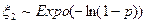 , то
, то 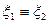 . Для построения алгоритма необходимо выполнить последовательность действий примера из пункта 4.6.2.
. Для построения алгоритма необходимо выполнить последовательность действий примера из пункта 4.6.2.
4.9.4. Моделирование гамма - распределения. Непрерывная случайная величина  имеет гамма - распределение с параметрами
имеет гамма - распределение с параметрами 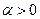 и
и 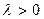 , если она имеет функцию плотности вероятностей вида
, если она имеет функцию плотности вероятностей вида
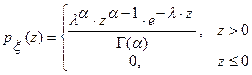 ,
,
Где 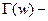 гамма-функция Эйлера, для
гамма-функция Эйлера, для  и
и 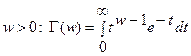 .
.
Свойства гамма - функции: 1) 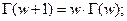 2)
2) 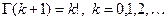 . Обозначение
. Обозначение 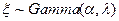 .
.
Частный случай гамма – распределения это распределение Эрланга 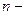 го порядка,когда
го порядка,когда 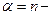 целое положительное число. Непрерывная случайная величина
целое положительное число. Непрерывная случайная величина  имеет распределение Эрланга
имеет распределение Эрланга 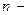 го порядка с параметрами
го порядка с параметрами  и
и 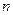 , если она имеет функцию плотности вероятностей вида
, если она имеет функцию плотности вероятностей вида
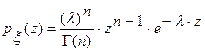 ,
,
Где 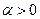 ,
, 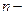 целое число.
целое число.
Теорема 7.Случайная величина 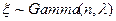 и ее плотность вероятностей равна
и ее плотность вероятностей равна
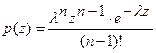 .
.
Тогда 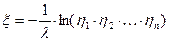 , где
, где 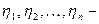 независимые случайные величины и
независимые случайные величины и 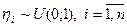 .
.
Доказательство. Доказательство проведем по индукции. При 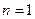 получаем
получаем 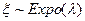 и тогда согласно пункта 4.6.2 имеем, что
и тогда согласно пункта 4.6.2 имеем, что 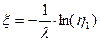 . Пусть утверждение теоремы верно при
. Пусть утверждение теоремы верно при 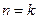 . Докажем, что оно также верно и для
. Докажем, что оно также верно и для 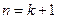 . Обозначим
. Обозначим 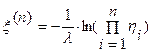 ,
, 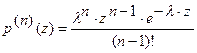 и
и 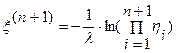 ,
, 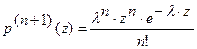 тогда
тогда 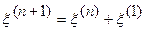 .
.
Воспользуемся правилом композиции плотностей независимых слагаемых
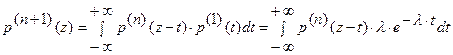
Воспользуемся индуктивным допущением
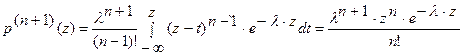
Теорема доказана.
Следствие.Пусть 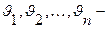 независимые случайные величины,
независимые случайные величины, 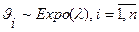 . Тогда
. Тогда 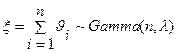 .
.
Примечание: Распределение Эрланга используется в теории массового обслуживания, описывая в ряде ситуаций распределение времен обслуживания.
4.9.5. Распределение Вейбулла. Непрерывная случайная величина  имеет распределение Вейбулла с параметрами
имеет распределение Вейбулла с параметрами 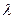 и
и  , если она имеет функцию распределения
, если она имеет функцию распределения 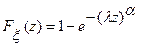 , где
, где 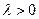 и
и 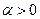 . Обозначают
. Обозначают 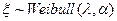 .
.
Для построения алгоритма моделирования, очевидно, что проще всего воспользоваться методом обратной функции.
Примечание: Распределение Вейбулла находит применение в статистической теории надежности при описании распределений времени без отказной работы.
4.9.6. Логнормальное распределение. Непрерывная случайная величина  имеет логнормальное распределение с параметрами
имеет логнормальное распределение с параметрами 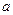 и
и 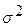 , если она имеет функцию плотности вероятностей вида
, если она имеет функцию плотности вероятностей вида
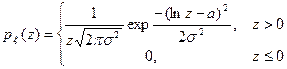 ,
,
где 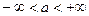 и
и 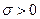 . Обозначают
. Обозначают 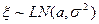 .
.
Воспользуемся свойством логнормального распределения – если 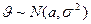 , то
, то 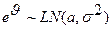 , следовательно
, следовательно 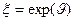 .
.
Алгоритм генерирования 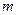 значений случайной величины
значений случайной величины 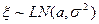 :
:
1. Генерируют 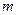 значение случайной величины
значение случайной величины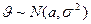 :
:  . Для этого можно использовать любой из алгоритмов описанных в пункте 4.7.
. Для этого можно использовать любой из алгоритмов описанных в пункте 4.7.
2. Проводят вычисления значений 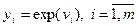 .
.
3. Полученная последовательность 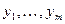 является выборкой объема
является выборкой объема 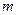 значений случайной величины имеющей логнормальное распределение с заданными параметрами.
значений случайной величины имеющей логнормальное распределение с заданными параметрами.
Примечание: Логнормальное распределение используется в моделях дробления частиц, в моделях роста.
4.9.7. Моделирование многомерного нормального распределения.Функция плотности вероятностей случайной величины 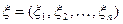 многомерного нормального распределения определяется как
многомерного нормального распределения определяется как
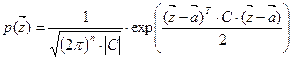 ,
,
для любого вектора 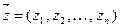 в
в 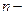 мерном вещественном пространстве;
мерном вещественном пространстве; 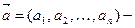 вектор средних значений, где
вектор средних значений, где 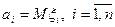 ;
; 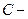 ковариационная матрица. Многомерное нормальное распределение обозначают как
ковариационная матрица. Многомерное нормальное распределение обозначают как  . Матрица
. Матрица  является симметричной и положительно определенной, и используя разложение Холецкого ее можно представить в виде
является симметричной и положительно определенной, и используя разложение Холецкого ее можно представить в виде 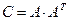 , где
, где 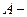 нижнетреугольная матрица.
нижнетреугольная матрица.
Алгоритм моделирования случайной величины 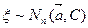 .
.
1. 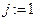 .
.
2. Генерируется по алгоритму пункта 4.7.1 вектор 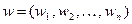 значений
значений 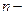 независимых и одинаково распределенных случайных величин
независимых и одинаково распределенных случайных величин 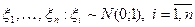 .
.
3. Вычисляют 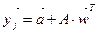 и
и 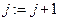 .
.
4. Если 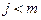 , то возвращаемся к пункту 2. В противном случае переходим к пункту 5.
, то возвращаемся к пункту 2. В противном случае переходим к пункту 5.
5. 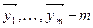 значений случайной величины
значений случайной величины  .
.
4.9.8. Моделирование многомерного логнормального распределения. Определим многомерное логнормальное распределение через его отношение к многомерному нормальному распределению: случайная величина 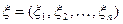 имеет логнормальное многомерное распределение, когда случайная величина
имеет логнормальное многомерное распределение, когда случайная величина 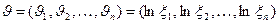 имеет многомерное нормальное распределение
имеет многомерное нормальное распределение  . Тогда случайный вектор многомерного логнормального распределения можно представить как
. Тогда случайный вектор многомерного логнормального распределения можно представить как 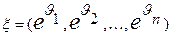 , где
, где 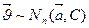 . Принятое обозначение
. Принятое обозначение 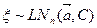
Алгоритм генерирования случайной величины 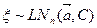 .
.
1. По алгоритму пункта 4.9.7 генерируем многомерную случайную величину 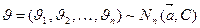 .
.
2. Возвращаем случайную величину  :
:
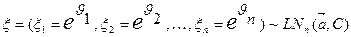
– Конец работы –
Эта тема принадлежит разделу:
СТАТИСТИЧЕСКОЕ МОДЕЛИРОВАНИЕ
СТАТИСТИЧЕСКОЕ МОДЕЛИРОВАНИЕ Статистическая модель Сущность статистического... Моделирование нормально распределенных случайных величин... Аналитические методы Тогда случайные...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: А) Непосредственное моделирование.
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов