Лекция 5. Производная и дифференциал
РАЗДЕЛ 1. Дифференциальное исчисление
Лекция 5. Производная и дифференциал
Понятие производной
Рис. 1 Точка М0 имеет координаты х0, у0=f(х0). Дадим переменной х приращение Dx и переместимся по графику из точки М0 в точку…Механический, физический и экономический смысл производной
. Пусть материальная точка движется по прямой в одном направлении. Обозначим S –…Уравнение касательной к кривой
y = kx + b (рис. 2). Определение 1. Касательной к графику называют прямую линию y = kx + b, которая наилучшим образом описывает исходную функцию z = z(x) в окрестности точки х0. «Наилучшим образом»…Геометрический смысл производной
у – у0 = k (x – х0) = f'(x0) (x – х0) или у = f'(x0) (x – х0) + у0. Таким образом, производная k = y'0 = f'(x0) есть тангенс угла наклона кривой… Для функции у = f(x) ее производная у' = f'(х) для каждого значения х равна угловому коэффициенту касательной к…Угол между кривыми
Рис. 8 К кривым f1(x) и f2(x) проведены касательные в их общей точке М(х0, у0), уравнения которых у = k1 x + b1 и у = k2 x +…Схема нахождения производной
Схема нахождения производной следует из ее определения:
1. Фиксируется значение х аргумента функции и выписывается начальное значение функции f(x).
2. В точке х аргументу придается приращение Δх ≠ 0 и выписывается новое (наращенное) значение функции f(x + Δx).
3. Вычисляется приращение функции Δy = f(x + Δx) – f(x).
4. Составляется отношение Δy / Δx.
5. Находится предел этого отношения при Δx ® 0 (если этот предел существует).
Пример 1. Найдем производную функции у = х2.
1. Фиксируем значение х аргумента функции и выписываем начальное значение функции f(x) = х2.
2. В точке х аргументу придаем приращение Δx ≠ 0 и выписываем новое значение функции f(x + Δx) = (х + Δx)2.
3. Вычисляем приращение функции: Δy = f(x + Δx) – f(x) = (х + Δx)2 – х2 =
= x2 + 2х Δx + (Δx)2 – x2 = Δx (2х + Δx).
4. Составляем отношение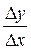 
= 2х + Δx.
5. Находим предел этого отношения при Δx ® 0:
у' =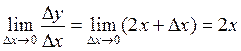 
.
Таким образом, получаем f'(х) = (х2)' = 2х.
Зависимость между дифференцируемостью и непрерывностью функции
Одно из определений непрерывности гласит, что функция называется непрерывной в точке, если в этой точке . Определение 1. Функция f(x) называетсядифференцируемой в точкех, если… Δy = A·Δx + α(Δx)·Δx,Таблица производных и правила дифференцирования
Правила дифференцирования:
21. 
Докажем 16-е утверждение в случае суммы:
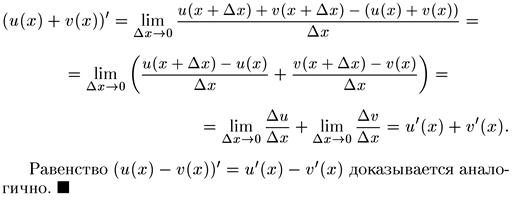
Правило 16 справедливо и для случая суммы любого конечного числа функций.
Докажем 19-е правило:
Дифференцирование обратной функции (п. 21). Если у = f(x) и х = g(y) – взаимно-обратные дифференцируемые функции, и y'x ≠ 0, то
,
т.е. производная обратной функции равна обратной величине производной данной функции.
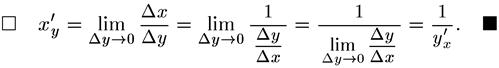
Пример 1. Если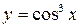 
, то, обозначив u=cos х, получим 
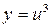. Тогда 
.
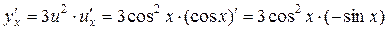Пример 2.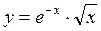
,
;
.
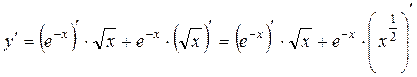Пример 3.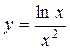 
, 
.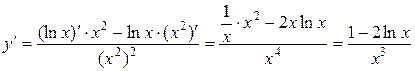