Понятие дифференциала функции

Пусть функция y = f(х) дифференцируема на отрезке [a, b], содержащем некоторую точку x. Тогда производная в этой точке x определятся равенством 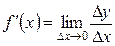. Из этого равенства (по теореме о связи функции, ее предела и бесконечно малой функции) следует, что

,

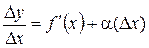где α(Δx) – б.м.ф. при 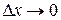. Отсюда

,

то есть приращение ∆у функции f(х), дифференцируемой в точке х, можно представить в виде суммы двух слагаемых, которые являются бесконечно малыми:

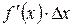– линейного члена относительно Δx

и α(Δx)· Δx – нелинейного члена.

При этом первое слагаемое есть б.м.ф. одного порядка с Δx, так как 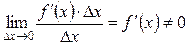, а второе слагаемое есть б.м.ф. более высокого порядка, чем Δx, так как .

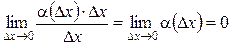Поэтому первое слагаемое 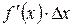называют главной частью приращения функции Δy.

Определение. Главная часть приращения функции f(х), линейная относительно приращения независимой переменной ∆х, называется дифференциалом функции f(х) в точке х, т.е. это произведение производной f'(x) на приращение независимой переменной ∆х:

dy =df(x)=f'(х)·∆х.

Замечание 1. Дифференциал функции составляет основную (главную) часть ее приращения, линейную относительно ∆х.

Например, приращение функции у = х² в точке х = 1, вызванное приращением аргумента Dх = 0,1, есть величина

∆у = (х + ∆х)² – х² = (1 + 0,1)² – 1² = 0,21.

Дифференциал функции в этой точке равен

dy = f'(х) · ∆х = 2 · х · ∆х = 2 · 1 · 0,1 = 0,2.

Таким образом, на нелинейную часть приращения α(Δx) · ∆х приходится величина 0,01 из полной величины приращения 0,21.

Замечание 2. Дифференциал аргумента совпадает с его приращением (dх=∆х), поэтому дифференциал функции записывается в виде

dy = df(х) = f'(x) dx,

т.е. дифференциал функции равен произведению производной этой функции на дифференциал независимой переменной.

Пример. Найти дифференциал функции f(x) = х.

Решение. df(x) = dx = х' ∆х = 1 · ∆х = ∆х.

Отсюда следует, что 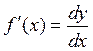, т.е. производную можно рассматривать как отношение дифференциала функции к дифференциалу независимой переменной.

Геометрический смысл дифференциала: dy = KN (рис. 7), т.е. дифференциал функции f(х) в точке x равен приращению ординаты касательной к графику функции в этой точке, когда x получит приращение Dх.

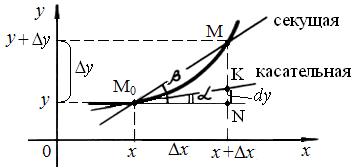
Рис. 7

При движении по графику функции f(х) из точки M₀ в точку M абсцисса переходит из точки х в точку х + Dх, а ордината получает приращение ∆у=f(х+∆х) – f(x). На рисунке это приращение ∆у равно отрезку NM. Если же двигаться из точки х в точку х + Dх по касательной, проведенной в точке М₀, то ордината получит приращение, равное отрезку KN. Из треугольника М₀KN получим величину этого приращения: KN = М₀N ·tgα.

Так как tgα = f'(x), а М₀N = ∆х, то KN = f'(x) · ∆х и KM = α(Δx) · Dх.

Приращение функции ∆y при малом приращении ∆x = dx по величине «очень мало» отличается от приращения по касательной, т.е. от дифференциала dy.

Так как касательная в точке М₀ почти совпадает с кривой в малой окрестности точки х, то при ∆х→0 разность (∆y – dy) = α(Δx) · Dх стремится к нулю быстрее, чем ∆x. Дифференциал функции dy отличается от её приращения ∆y на бесконечно малую величину более высокого порядка по сравнению с ∆x. Это обстоятельство используется в приближенных вычислениях.