рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Математика
- /
- Вид работы: Лекции
- /
- Механический, физический и экономический смысл производной
Реферат Курсовая Конспект
Механический, физический и экономический смысл производной
Механический, физический и экономический смысл производной - Лекция, раздел Математика, Лекция 5. Производная и дифференциал Механический Смысл Производной: Скорость Прямолинейного Движ...
Механический смысл производной: скорость прямолинейного движения материальной точки в момент времени t0 есть производная от пути по времени:
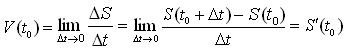 .
.
Пусть материальная точка движется по прямой в одном направлении. Обозначим S – путь, пройденный точкой, а t – время. Путь, пройденный точкой за время t, зависит от t и изменяется по некоторому закону S=S(t). Поставим задачу определить скорость материальной точки V0 в некоторый момент времени t0. Для этого рассмотрим другой момент времени по прошествии отрезка Dt, т.е. момент t0+Dt. К моменту t0 пройденный точкой путь составит S(t0); к моменту t0+Dt точка пройдет путь S(t0+Dt). За промежуток времени Dt точка прошла путь DS = S(t0+Dt) – S(t0). Средняя скорость движения за время Dt составит отношение  . Эта средняя скорость отличается от мгновенной скорости в момент t0, и величина Vcp тем ближе к скорости V0, чем меньше промежуток Dt. Устремим Dt к нулю (Dt®0). Тогда предел, к которому стремится средняя скорость, является скоростью точки V0 в момент t0:
. Эта средняя скорость отличается от мгновенной скорости в момент t0, и величина Vcp тем ближе к скорости V0, чем меньше промежуток Dt. Устремим Dt к нулю (Dt®0). Тогда предел, к которому стремится средняя скорость, является скоростью точки V0 в момент t0:
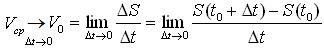
Здесь рассматривается предел отношения приращения пути DS к приращению времени Dt.
Физический смысл производной: Обобщая предыдущий закон V = S'(t), можно сказать, что если функция у = f(t) описывает физический процесс, меняющийся со временем t, то производная у' = f'(t0) есть скорость протекания этого процесса в момент t0.
Экономический смысл производной.
Производительность труда в момент t0 – предельное значение средней производительности за период времени от t0 до t0 + Δt при Δt ® 0, т. е.

Здесь ΔQ – количество произведенной продукции за интервал времени Δt. Производительность труда u – скорость роста объема продукции Q.
Предельный продукт. Пусть функция Q(x) – зависимость количества произведенной продукции от величины затрат ресурса х. Отношение  – средняя величина продукта, соответствующая величине затрат в размере Δх. Предельный (маржинальный) продукт при затратах ресурса х0:
– средняя величина продукта, соответствующая величине затрат в размере Δх. Предельный (маржинальный) продукт при затратах ресурса х0:
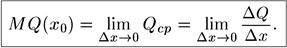
– Конец работы –
Эта тема принадлежит разделу:
Лекция 5. Производная и дифференциал
Лекция Производная и дифференциал Понятие производной Рис... Схема нахождения производной... Схема нахождения производной следует из ее определения...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Механический, физический и экономический смысл производной
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов