рефераты конспекты курсовые дипломные лекции шпоры
Реферат Курсовая Конспект
Предел функции в бесконечности
Предел функции в бесконечности - Лекция, раздел Механика, РАЗДЕЛ 1. Дифференциальное исчисление Определение Такое Же, Как И В Точке А, Только Значения X Могут ...
Определение такое же, как и в точке а, только значения x могут становиться сколь угодно большими, т.е. рассматривается предел функции в бесконечности (x →а=∞). Окрестностью точки ∞ здесь считаем множнство достаточно больших значений х.
Определение.Число b называется пределом функции у=f(x) при х, стремящемся к бесконечности (x→∞), если для любого сколь угодно малого числа ε>0 можно указать такое число S(ε)>0, что при всех допустимых значениях x таких, что |х|>S, выполняется неравенство |f(x) - b| < ε. Этот предел обозначается 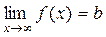 .
.
Данное определение при x→∞ предполагает неограниченное возрастание х по абсолютной величине. Неравенству |х| > S равносильно х > S и х < -S.
Неравенство х > S определяет интервал (S; +∞), который называется окрестностью в точке а = +∞ при произвольном фиксированном S. Тогда можно сформулировать понятие предела при x →+∞.
Неравенство х < -S определяет интервал (-S; -∞), который называется окрестностью в точке а = -∞ при произвольном фиксированном -S. Тогда можно сформулировать понятие предела при x → -∞.
Рассмотрим геометрический смысл предела функции на +бесконечности х® +∞ (рис.3).
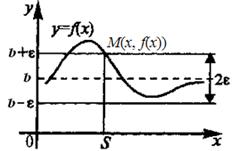
Рис.3.
Зафиксируем на оси 0Y ε-окрестность и изобразим горизонтальную полосу, ограниченную прямыми у = b+ε, у = b-ε. Число b будет пределом функции f(x) при х ® +∞, если при перемещении по оси ОХ аргумента х вправо с момента S (т.е. на интервале х є (S; +∞)) график функции f(x) попадает внутрь полосы, ограниченной ε-окрестностью числа b.
При уменьшении числа ε интервал (b-ε; b+ε) будет стягиваться к числу b, а рубеж S, соответствующий числу ε, будет находиться правее. Как бы ни было мало число ε > 0, всегда найдется такое число S, что при всех допустимых значениях x > S точка графика M(x, f(x)) отклоняется от горизонтальной линии у=b меньше, чем на величину ε, т.е. выполняется |f(x) – b| < ε. Это и доказывает, что 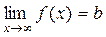 .
.
Аналогично определяется предел при x → -∞.
Дадим в общих словах понятие предела функции у = f(х) в бесконечности.
Определение.Число b называется пределом функции у = f(x) при x → ∞, если значения функции сколь угодно близко приближаются к числу b, когда значения х становятся сколь угодно большими: 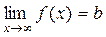 .
.
Пример 1. Доказать, что 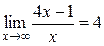 .
.
Решение. Функция f(x)= 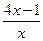 определена всюду, кроме точки a = 0.
определена всюду, кроме точки a = 0.
Согласно определению |f(x)-b|<ε, рассмотрим неравенство | 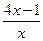 - 4| < ε или |
- 4| < ε или | 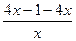 | = |
| = | 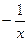 | = |
| = |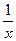 | < ε или |x| >
| < ε или |x| > 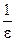 . Таким образом, для любого ε > 0 можно взять такое число S=
. Таким образом, для любого ε > 0 можно взять такое число S=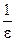 , что для всех х, удовлетворяющих неравенству |х|> S =
, что для всех х, удовлетворяющих неравенству |х|> S = 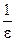 , будет справедливо неравенство |f(х) - 4| = |
, будет справедливо неравенство |f(х) - 4| = |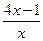 - 4| < ε. Это и означает, что
- 4| < ε. Это и означает, что 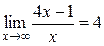 .
.
Замечание 1. Понятие предела функции в точке a вводится только для предельных точек a области определения функции, ибо рассматривает значения х ≠ а в некоторой окрестности точки а. При этом функция может быть и не определена в точке а, т.е., вообще говоря, a не обязательно принадлежит D. При рассмотрении 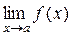 предполагают, что х стремится к а, но не достигает значения а. Поэтому наличие или отсутствие предела при x→а определяется поведением функции в окрестности точки а и не связано со значением функции (или его отсутствием) в самой точке а.
предполагают, что х стремится к а, но не достигает значения а. Поэтому наличие или отсутствие предела при x→а определяется поведением функции в окрестности точки а и не связано со значением функции (или его отсутствием) в самой точке а.
Замечание 2. Переменная х может стремиться к числу a не только по произвольному закону, но и, например, только справа: х®а+0, или только слева: х®а-0. В этом случае говорят об односторонних пределах функции соответственно справа 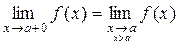 и слева
и слева 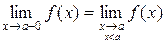 .
.
Если односторонние пределы функции различны, т.е. 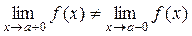 , то предела функции при х ® а не существует.
, то предела функции при х ® а не существует.
Пример 2.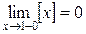 ,
, 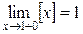 . Здесь [х] – целая часть х. Односторонние пределы функции у=[х] не совпадают, значит, эта функция не имеет предела при х®1.
. Здесь [х] – целая часть х. Односторонние пределы функции у=[х] не совпадают, значит, эта функция не имеет предела при х®1.
Переменная х может стремиться к бесконечности как в сторону отрицательных, так и положительных значений: х®∞; х®-∞; х®+∞.
Значения функции могут приближаться к числу b по произвольному закону (y®b), сверху (y®b+0), снизу (y®b+0).
Функция может неограниченно возрастать (y®+∞), убывать (y®-∞), неограниченно возрастать по модулю (|y|®+∞).
Всего может существовать 36 определений пределов функции:
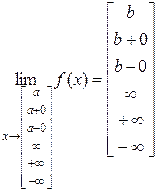
Пример 3. Можно написать: 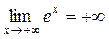 или
или  . Вторая запись оставляет открытым вопрос о знаке функции ех. Но нельзя под знаком предела вместо х ® +∞ написать х ® ∞. Последняя запись включала бы и тот случай, когда х ® -∞, что было бы неверно, так как
. Вторая запись оставляет открытым вопрос о знаке функции ех. Но нельзя под знаком предела вместо х ® +∞ написать х ® ∞. Последняя запись включала бы и тот случай, когда х ® -∞, что было бы неверно, так как 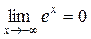 .
.
– Конец работы –
Эта тема принадлежит разделу:
РАЗДЕЛ 1. Дифференциальное исчисление
Лекции и Предел функции Понятие предела функции Пусть функция... Свойства бесконечно больших величин... Произведение бесконечно большой величины на функцию имеющую ненулевой предел бесконечно большая величина...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Предел функции в бесконечности
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов