рефераты конспекты курсовые дипломные лекции шпоры

  • Раздел Механика
  •  / 
  • Вид работы: Лекции
  •  / 
  • Основные свойства пределов (теоремы о пределах)

Реферат Курсовая Конспект

Основные свойства пределов (теоремы о пределах)

Основные свойства пределов (теоремы о пределах) - Лекция, раздел Механика, РАЗДЕЛ 1. Дифференциальное исчисление 1. Функция Не Может Иметь Более Одного Предела. Докажем Это С...

1. Функция не может иметь более одного предела.

Докажем это свойство. Предположим противное, т.е. что функция f(x) имеет два разных предела b и с:

, , b ≠ c.

Поскольку утверждения «число b есть предел величины у» и «разность у – b есть бесконечно малая величина» равнозначны, то величины

α(x) = f(x) – b, β(x) = f(x) – c

бесконечно малы при х → а. Вычитая почленно эти равенства, получим

α(x) – β(x) = с – b ≠ 0,

что невозможно, поскольку переходя в этом равенстве к пределу при х → а, имеем: . Следовательно, предположение о существовании второго предела неверно.

2. Предел постоянной величины y = с есть само число с: lim с = с.

Пусть y, …, z, u, v – функции, для которых существуют пределы в точке а (не исключаем случая а = ∞).

3. Предел алгебраической суммы (т.е. сумма или разность) конечного числа функций y, u, ..., z равен такой же сумме пределов этих функций:

lim(y ± u ±....± z) = limy ± limu ±....± limz;

4. Предел произведения конечного числа функций y, u, ..., z равен произведению пределов этих функций:

lim(y · u ·...· z) = limy · limu ·...· limz.

В частности, постоянный множитель можно выносить за знак предела, т. е.

5. Предел частного равен частному пределов:

.

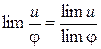Если предел делителя равен нулю (limj = 0), а limu = с ≠ 0, то запись 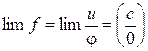следует понимать в том смысле, что . Таким образом, будем считать, что .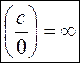

Аналогичные записи можно применять и для односторонних пределов:

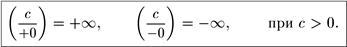
Пример 1. .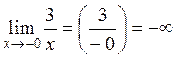

Если limu=0 и limj=0, теорема неприменима, так как выражение является неопределенным. Но теорема остается верной. «Сокращать» на нуль и писать 1 вместо нельзя. Этот символ закрывает прямой путь подстановки и заставляет искать путь раскрытия этой неопределенности (например, с помощью сокращения общих множителей).

6. Пусть y=f(u), u=φ(x). Тогда y=f(φ(x)) – сложная функция.

Если , , 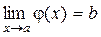то предел сложной функции

.

7. Если limf(x) = b > 0, limg(x) = c, то имеет место соотношение

lim(f(x))g(x) = (lim(f(x))limg(x) = bc.

8. Если в некоторой окрестности точки а (окрестностью точки ∞ считаем множество достаточно больших х) выполняется нестрогое неравенство f(x)≤g(x), то для соответствующих пределов выполнено нестрогое неравенство:

.

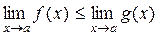(Заметим, что если в окрестности точки а выполняется строгое неравенство f(x)<g(x), то утверждение теоремы сохраняет свою силу, так как из строгого неравенства в пределе получается, вообще говоря, нестрогое).

9. Если в некоторой окрестности точки а функция f(x) заключена между двумя функциями и(х) и v(x), имеющими одинаковый предел b при х → а, то функция f(x) имеет тот же предел b:

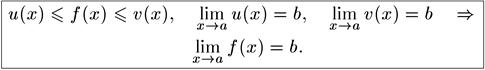
Свойства пределов облегчают их вычисление.

Пример 2. Найти предел функции при x®1.

Решение. Воспользуемся свойствами пределов и найдем отдельно пределы числителя и знаменателя:

=7∙1-4∙1+2=5,

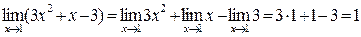
Применяя свойство 3, получим предел дроби: .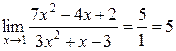

Непосредственное применение свойств пределов сразу привело к получению ответа.

На практике такие случаи встречаются крайне редко, а потому, прежде чем применять теоремы о пределах, приходится тождественно преобразовывать данную функцию.

Пример 3. Найти предел функции при x®¥.

При этом и числитель, и знаменатель также стремятся к бесконечности. Символически этот случай обозначают [¥/¥] и называют «неопределенностьютипа [¥/¥]». Очевидно, что непосредственно применить теорему о пределе частного здесь нельзя. Для раскрытия неопределенности преобразуем предварительно данную дробь, разделив и числитель, и знаменатель на х3 (старшую степень знаменателя):

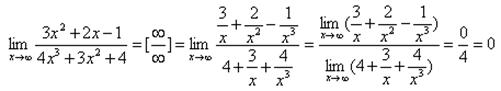
Величины 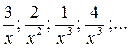– бесконечно малые при x®¥, и их пределы равны нулю. Итак, предел функции у равен нулю, следовательно, при x®¥ у – бесконечно малая функция.

Пример 4. Найти .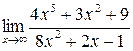

Решение. Вновь получили неопределенность типа [¥/¥].

Применим только что использованный прием, и числитель, и знаменатель поделим на х5 (старшую степень числителя):

.

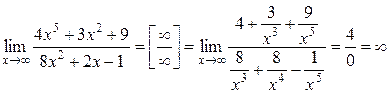Предел числителя в полученной дроби равен 4, а предел знаменателя равен нулю, знаменатель при x®¥ - бесконечно малая величина. Вся дробь является величиной, обратной бесконечно малой, т.е. бесконечно большой, и ее предел равен бесконечности.

Пример 5. Найти . Решение:

 
Развернуть
Открыть в широком формате

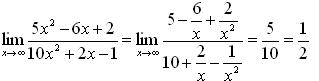
– Конец работы –

Эта тема принадлежит разделу:

РАЗДЕЛ 1. Дифференциальное исчисление

Лекции и Предел функции Понятие предела функции Пусть функция... Свойства бесконечно больших величин... Произведение бесконечно большой величины на функцию имеющую ненулевой предел бесконечно большая величина...

Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Основные свойства пределов (теоремы о пределах)

Что будем делать с полученным материалом:

Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:

Все темы данного раздела:

Понятие предела функции
Понятие предела является фундаментальным в математическом анализе. С его помощью вводятся понятия производной, интеграла, непрерывности и т.д. Пусть функция f(x) определена в

Предел функции в бесконечности
Определение такое же, как и в точке а, только значения x могут становиться сколь угодно большими, т.е. рассматривается предел функции в бесконечности (x →а=∞

Бесконечно малые величины
  Определение. Функция называется a(х) называется бесконечно малой величиной в какой-то точке a, если она имеет нулевой предел в

Свойства бесконечно малых величин
1. Сумма бесконечно малых величин бесконечно мала: α(x) = α1(x) + α2(x). Пример 3. α(x) = 4

Бесконечно большие величины
  Определение. Функция f(x) называется бесконечно большой величиной в какой-то точке a прикосновения множества допустимых

Связь между бесконечно большой и бесконечно малой функциями
Величина, обратная бесконечно большой величине при х®а, есть бесконечно малая, и наоборот, т.е. при х®а (х®∞)

Виды неопределенностей
Если предельные значения оказываются равными 0 или ∞, то могут возникнуть неопределенности вида: . Соотн

Первый и второй замечательные пределы
  1-й замечательный предел: . Означает, что sinх ~ х (эквивал

Сравнение бесконечно малых
Пусть α(х) и β(х) – бесконечно малые при х®а. Их частное может и не быть бесконечно малым. Пример 1. α(х)=6х; ^

Принцип замены эквивалентных
Если функции α(х) и β(х) являются бесконечно малыми при х®а, и если α(х) ~ γ(х), β(х) ~ η(х), то

Хотите получать на электронную почту самые свежие новости?
Education Insider Sample
Подпишитесь на Нашу рассылку
Наша политика приватности обеспечивает 100% безопасность и анонимность Ваших E-Mail
Реклама
Соответствующий теме материал
  • Похожее
  • Популярное
  • Облако тегов
  • Здесь
  • Временно
  • Пусто
Теги