Измерение в квантовой механике. Соотношение неопределенности

В связи со специфическими особенностями микрообъектов особенного значения приобретает вопрос об измерениях в квантовой механике. Процесс измерения включает в себя наблюдаемую систему, измерительный прибор и наблюдателя.

В классической механике все три составных измерения носят макроскопический характер, поэтому взаимодействие между ними можно сделать сколько угодно малым. Следовательно, измерительный прибор не влияет на систему, которая наблюдается и результаты измерений предсказуемы.

В микромире взаимодействие между наблюдаемой системой и измерительным прибором нельзя сделать сколько угодно малым, чтобы состояние наблюдаемой системы не изменилось в процессе измерения, поскольку измерительный прибор имеет макроскопическую природу, а наблюдаемая система носит микроскопический характер. Поэтому допустить, что наблюдатель может предсказать |результаты эксперимента уже нельзя.

Из-за взаимодействия измерительного прибора и наблюдаемой системы некоторые измерения несовместимы: осуществление одного измерения исключает возможность другого. Например, нельзя одновременно определить точные значения координаты и соответствующего ей импульса. И это не экспериментальная трудность, связанная с инструментальными погрешностями, а фундаментальный закон природы, который выражается принципом неопределенностей. Впервые он был сформулирован Гайзенбергом в 1927 г.

Согласно принципу неопределенности не существуют такие состояния физической системы, в которых две динамические переменные имели бы вполне определенные значения, если эти переменные канонически сопряжены друг другу в духе гамильтонова формализма, то есть входят в уравнение Гамильтона^[27]. Примером канонично связанных величин является координата центра инерции системы и соответствующая этой координате компонента импульса, угол поворота системы вокруг некоторой оси и проекция момента количества движения на эту ось.

Измеряя одновременно импульс и соответствующую ему координату, будем получать разброс около средних значений. Разброс характеризуется дисперсией. Связь между дисперсией координаты и дисперсией импульса устанавливает соотношение Гайзенберга

. (1.4)

Чаще запись соотношения неопределенности встречается в упрощенной форме

.

Аналогичное соотношение можно записать для энергии и времени, хоть последнее является параметром, а не динамической переменной:

.

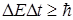Одна из возможных расшифровок последнего соотношения следующая. Под 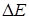можно понимать неопределенность значения энергии нестационарного состояния замкнутой системы, если физические величины системы существенно изменяются за промежуток времени 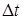. Например, возбужденные состояния атомов квазистационарны. Если считать 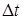средним временем жизни возбужденного состояния атома, то 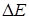представляет среднюю ширину его энергетического уровня.

В связи с малостью постоянной 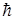принцип неопределенности представляет интерес главным образом для систем атомного размера.

Вернемся к измерениям в квантовой механике. Поскольку измерительный прибор изменяет состояние наблюдаемой системы, то повторить опыт над одним и тем же объектом невозможно. Необходимо после каждого измерения либо возвращать объект в начальное состояние, либо же проводить опыт с другими объектами, которые находятся в таком же состоянии.

В квантовой механике совокупность тождественных частиц, которые находятся в одинаковых состояниях, называется ансамблем.

Таким образом, измерения в квантовой механике осуществляется над ансамблем. Измерения бывают воспроизводимыми (если результаты опыта повторяются) и невоспроизводимыми (результаты не повторяются). В связи с этим состояния объектов в квантовой механики можно разделить на два класса: состояния, в которых физическая величина имеет определенное значение, и состояния, в которых физическая величина не имеет определенного значения.