рефераты конспекты курсовые дипломные лекции шпоры
Реферат Курсовая Конспект
Микрочастица в потенциальной яме конечной глубины
Микрочастица в потенциальной яме конечной глубины - Лекция, раздел Механика, Черняков Э.И. Лекции по дисциплине Физические основы электронной техники. Квантовая механика Потенциальное Поле Ямы Имеет Вид ...
Потенциальное поле ямы имеет вид  при
при 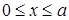 ,
, 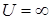 при
при 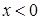 и
и  при
при  (рис.1.8, а). Частица, которая находится в такой яме с энергией
(рис.1.8, а). Частица, которая находится в такой яме с энергией  , будет все время с ней связана.
, будет все время с ней связана.
Решение стационарного уравнения Шредингера имеет вид
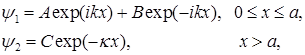 (1.143)
(1.143)
где 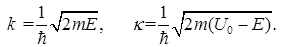 (1.144)
(1.144)
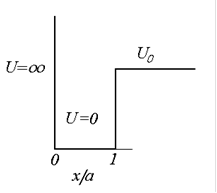
|
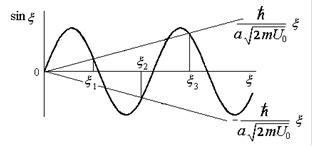
|
| а | б |
| Рис.2.8. Потенциальная яма конечной глубины (а) и графоаналитическое решение дисперсионного уравнения (б) |
Воспользовавшись условиями
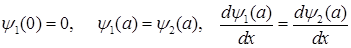 , (1.145)
, (1.145)
получим уравнение
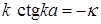 . (1.146)
. (1.146)
Преобразуем (1.146) в уравнение более удобное для анализа:
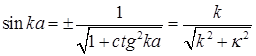 .
.
Обозначим  и с учетом
и с учетом 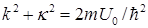 , получим
, получим
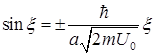 . (1.147)
. (1.147)
В качестве решения берем не все точки пересечения синусоиды с прямыми, а только те, знак которых согласуется со знаком первичного уравнения (1.146). Этим значением 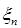 отвечает конечное число собственных значений энергии
отвечает конечное число собственных значений энергии
 . (1.148)
. (1.148)
Если яма мелкая или достаточно узкая, то может случиться, что решение уравнения (1.146) отсутствует, то есть частица не может удержаться внутри ямы.
В классической механике частица с энергией  не может выйти за пределы ямы. В квантовой механике существует вероятность найти частицу за пределами ямы, если даже
не может выйти за пределы ямы. В квантовой механике существует вероятность найти частицу за пределами ямы, если даже  . Как пример, на рис.1.9 показаны волновая функция и распределение плотности вероятности для основного и возбужденного состояний электрона в потенциальной яме конечной глубины.
. Как пример, на рис.1.9 показаны волновая функция и распределение плотности вероятности для основного и возбужденного состояний электрона в потенциальной яме конечной глубины.

| 
|
| а | б |
| Рис.1.9. Волновая функция и распределение плотности вероятности для основного (а) (~7еВ) и возбужденного (б) (~27еВ) состояний электрона в потенциальной яме (а=0,2 нм, U0=40 эВ). |
– Конец работы –
Эта тема принадлежит разделу:
Черняков Э.И. Лекции по дисциплине Физические основы электронной техники. Квантовая механика
Черняков Э И Лекции по дисциплине... Физические основы электронной техники Квантовая механика ВВЕДЕНИЕ...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Микрочастица в потенциальной яме конечной глубины
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов