рефераты конспекты курсовые дипломные лекции шпоры

Раздел Механика
/
Вид работы: Лекции
/
Свободное движение микрочастицы

Реферат Курсовая Конспект

Выберите учебное заведение

Свободное движение микрочастицы

Свободное движение микрочастицы - Лекция, раздел Механика, Черняков Э.И. Лекции по дисциплине Физические основы электронной техники. Квантовая механика Рассмотрим Некоторые Самые Простые Случаи Движения Микрочасти...

Рассмотрим некоторые самые простые случаи движения микрочастицы в потенциальных полях. Начнем со свободного движения.

Оператор Гамильтона в этом случае имеет вид

Представляя волновую функцию в виде

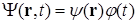(1.61))

и используя метод разделения переменных, получим функцию , которая зависит от времени

, (1.62)

и амплитудное уравнение Шредингера (или уравнение для стационарных состояний)

. (1.63)

Систему координат выбираем таким образом, чтобы направление движения частицы совпадало с осью . Тогда решение уравнения (1.63) будет иметь вид

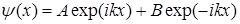, (1.64)

где 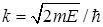(по физическому содержанием это волновой вектор).

Значения энергии, как видно из (1.64) оказываются двукратно вырожденными. Это вырождение снимается, если потребовать, чтобы кроме энергии в этом состоянии имела определенные значения еще какая-либо физическая величина, например, импульс. Тогда частице, которая движется в положительном направлении оси , соответствуют импульс 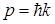и энергия 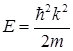. Им отвечает собственная волновая функция

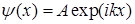. (1.65)

Ввиду непрерывности энергетического спектра нормировать (1.65) следует не на единицу, а на 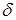- функцию

. (1.66)

Используя интегральное представление 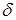- функции

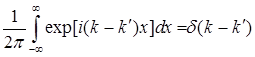получим для коэффициента .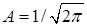

Следовательно, волновая функция свободной микрочастицы (волна де Бройля) имеет вид

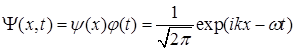. (1.67)

Развернуть

Открыть в широком формате

– Конец работы –

Эта тема принадлежит разделу:

Черняков Э.И. Лекции по дисциплине Физические основы электронной техники. Квантовая механика

Черняков Э И Лекции по дисциплине... Физические основы электронной техники Квантовая механика ВВЕДЕНИЕ...

Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Свободное движение микрочастицы

Что будем делать с полученным материалом:

Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:

Все темы данного раздела:

Волны де Бройля
Квантовая механика является разделом теоретической физики, который изучает движение частиц в области микромира, то есть объясняет явления, которые происходят в объемах с линейными размерами

Измерение в квантовой механике. Соотношение неопределенности
В связи со специфическими особенностями микрообъектов особенного значения приобретает вопрос об измерениях в квантовой механике. Процесс измерения включает в себя наблюдаемую систему, измерительный

Волновая функция
Для полного описания состояния системы (частицы) необходимо столько физических величин, сколько степеней свободы имеет система. Совокупность физических величин, которые полностью определяют сост

Принцип суперпозиции
В классической механике известен принцип суперпозиции. Примером могут служить колебания струны. Наравне с колебаниями чистого типа возможна суперпозиция колебаний различных типов. В

Закон сохранения числа микрочастиц
Получим из уравнения Шредингера закон сохранения числа частиц. Запишем уравнение Шредингера и комплексно сопряженное ему

Рассеяние микрочастицы на потенциальной ступени
Потенциальное поле при

Туннельный эффект
Большой интерес вызывает задача прохождения частицы через потенциальный барьер конечной протяжности. Определим коэффициент прозрачности

Микрочастица в потенциальной яме
Сделаем предварительно замечание: непрерывность производной от волновой функции не имеет места, если за некоторой поверхностью потенциальная энергия обращается в бесконечность. В эт

Квантово-механический осциллятор
Атомы в молекулах и кристаллах осуществляют колебания возле положения равновесия. При малых смещениях на атом действует сила, которая пропорциональная смещению

Микрочастица в потенциальной яме конечной глубины
Потенциальное поле ямы имеет вид при

Микрочастица в связанных потенциальных ямах
Задача о движении частицы (электрона) в связанных потенциальных ямах (рис.1.10) оказывается полезной для понимания природы ковалентных связей в молекулах. Решения будем искать в предположе