рефераты конспекты курсовые дипломные лекции шпоры
Реферат Курсовая Конспект
Рассеяние микрочастицы на потенциальной ступени
Рассеяние микрочастицы на потенциальной ступени - Лекция, раздел Механика, Черняков Э.И. Лекции по дисциплине Физические основы электронной техники. Квантовая механика Потенциальное Поле ...
Потенциальное поле  при
при 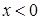 и
и  при
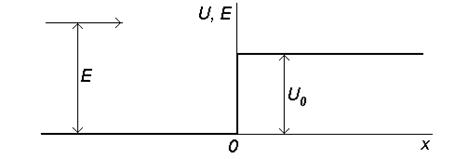
при  называют потенциальной ступенькой или бесконечно протяжным потенциальным барьером (рис.1.2, а). Пусть на барьер падает монохроматический поток микрочастиц. Коэффициент рассеяния (отражения) барьера определяется как отношение потока отраженного к потоку падающему, а коэффициент прозрачности (прохождения) – отношением прошедшего потока к потоку падающему.
называют потенциальной ступенькой или бесконечно протяжным потенциальным барьером (рис.1.2, а). Пусть на барьер падает монохроматический поток микрочастиц. Коэффициент рассеяния (отражения) барьера определяется как отношение потока отраженного к потоку падающему, а коэффициент прозрачности (прохождения) – отношением прошедшего потока к потоку падающему.
Поскольку задача стационарная (высота барьера не зависит от времени), определение состояний частицы сводится к решению стационарного уравнения Шредингера, которое для одномерного случая принимает вид
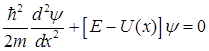 . (1.68)
. (1.68)
Сначала рассмотрим низкий барьер (E >U0). Решения для первой (x<0) и второй (x>0) областей имеют вид
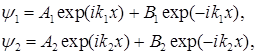 (1.69)
(1.69)
где
 и
и 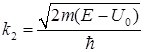 . (1.70)
. (1.70)
Учитывая однородность среды в области 2, амплитуду 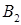 „встречной” волны следует считать равной нулю (
„встречной” волны следует считать равной нулю ( ).
).
Если учесть, что для стационарных состояний волновая функция гармонически зависит от времени, то  представляет собой суперпозицию падающей
представляет собой суперпозицию падающей 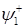 и отраженной
и отраженной 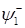 волн де Бройля
волн де Бройля
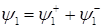 , (1.71)
, (1.71)
а  описывает волну де Бройля частицы, которая движется над барьером,
описывает волну де Бройля частицы, которая движется над барьером,
 . (1.72)
. (1.72)
Физический интерес представляют коэффициенты прохождения  и отражения
и отражения 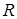 , которые определяются отношением плотности потока частиц, которые прошли и которые отразились, к плотности потока частиц, которые падают на барьер.
, которые определяются отношением плотности потока частиц, которые прошли и которые отразились, к плотности потока частиц, которые падают на барьер.
Для расчетов  и
и 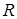 воспользуемся понятиям вектора плотности потока вероятности (1.50), который в одномерном случае имеет вид
воспользуемся понятиям вектора плотности потока вероятности (1.50), который в одномерном случае имеет вид
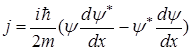 . (1.73)
. (1.73)
С учетом (1.73) коэффициент прохождения (прозрачности) равен
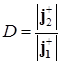 , (1.74)
, (1.74)
а коэффициент отражения
 . (1.75)
. (1.75)
 а
а
|
 б
б
|
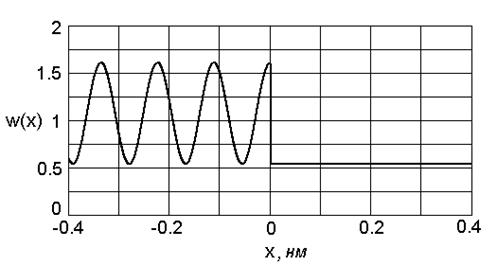
| Рис.1.2. Энергетическая диаграмма потенциального выступа (а) и графики распределения плотности вероятности (U0=20 эВ; электрон с энергией E=30 эВ) (б) |
Вычислим величину вектора плотности потока вероятности в области 2, для чего подставим (1.72) в (1.73):
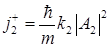 . (1.76)
. (1.76)
Аналогично в области 1 плотность потока вероятности частиц, которые падают на барьер, может быть предоставлена в виде
 , (1.77)
, (1.77)
а плотность потока вероятности частиц, которые отражаются барьером,
 . (1.78)
. (1.78)
С учетом (1.76) – (1.78) имеем
 (1.79)
(1.79)
и
 . (1.80)
. (1.80)
Таким образом, для определения коэффициентов прохождения и отражения необходимо определить амплитуды 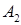 и
и  через амплитуду
через амплитуду 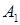 . Для этого воспользуемся условием непрерывности волновой функции на границе двух сред (
. Для этого воспользуемся условием непрерывности волновой функции на границе двух сред ( ):
):
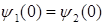 , (1.81)
, (1.81)
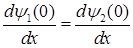 . (1.82)
. (1.82)
Воспользовавшись (1.69), (1.72), (1.81) и (1.82), получим
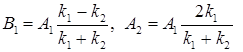 , (1.83)
, (1.83)
откуда с учетом (1.70), (1.79) и (1.80)
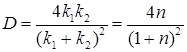 , (1.84)
, (1.84)
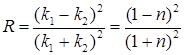 , (1.85)
, (1.85)
где  – коэффициент преломления барьера
– коэффициент преломления барьера
 . (1.86)
. (1.86)
Из (1.84) и (1.85) видно, что автоматически выполняется соотношение
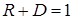 , (1.87)
, (1.87)
которое представляет собой закон сохранения числа частиц.
Плотность потока вероятности частиц при x>0 равна
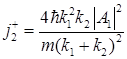 . (1.88)
. (1.88)
Полученные результаты сильно отличаются от классических. Согласно законам классической механики частица, которая имеет энергию  , всегда проникнет в область 2.
, всегда проникнет в область 2.
Согласно законам квантовой механики при  имеет место вероятность отражения частицы от потенциального барьера, и поэтому в области 1 будет наблюдаться встречный поток отраженных частиц
имеет место вероятность отражения частицы от потенциального барьера, и поэтому в области 1 будет наблюдаться встречный поток отраженных частиц .
.
Для частиц, которые движутся к барьеру с 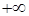 , коэффициенты
, коэффициенты  и
и 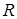 также могут быть обсчитаны по формулам (1.84) и (1.85). Но изменение направления движения приводит к изменению фазы отраженной волны. В нашем случае для частиц, которые падают на барьер слева, отражение происходит в фазе с падающей волной, а при движении справа – в противофазе. Изменение направления движения приводит к изменению фазы отраженной волны.
также могут быть обсчитаны по формулам (1.84) и (1.85). Но изменение направления движения приводит к изменению фазы отраженной волны. В нашем случае для частиц, которые падают на барьер слева, отражение происходит в фазе с падающей волной, а при движении справа – в противофазе. Изменение направления движения приводит к изменению фазы отраженной волны.
Рассмотрим случай, когда энергия частицы меньше высоты барьера  . В этом случае коэффициент
. В этом случае коэффициент  будет мнимым
будет мнимым
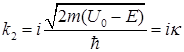 , (1.89)
, (1.89)
и коэффициент отражения для высокого барьера будет равняться единице
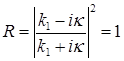 . (1.90)
. (1.90)
Таким образом, при  все частицы отражаются от потенциального барьера и в области 2 поток частиц отсутствует. Однако имеет место вероятность обнаружить частицу в области барьера (
все частицы отражаются от потенциального барьера и в области 2 поток частиц отсутствует. Однако имеет место вероятность обнаружить частицу в области барьера (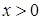 )
)
 . (1.91)
. (1.91)
Частица якобы проходит в потенциальный барьер и возвращается назад. При этом между падающей и отраженной волнами возникает фазовый сдвиг
 . (1.92)
. (1.92)
Эффективная глубина проникновения в барьер, при которой вероятность обнаружения частицы отличается от нуля, имеет порядок величины  . При
. При 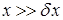 плотность вероятности (1.91) будет экспоненциально малой величиной.
плотность вероятности (1.91) будет экспоненциально малой величиной.
Сделаем оценку глубины проникновения электрона в потенциальный барьер, если 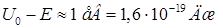 . Для
. Для 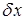 имеем
имеем
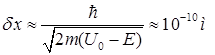 .
.
Следовательно, эффект будет заметным только в области микроскопических размеров.
Для обнаружения частицы в области 2 мы должны локализовать ее в некотором малом интервале  . При этом, локализуя частицу, мы изменяем ее состояние (энергию). Действительно, из соотношения неопределенности имеем
. При этом, локализуя частицу, мы изменяем ее состояние (энергию). Действительно, из соотношения неопределенности имеем  . С неопределенностью импульса связана неопределенность кинетической энергии частицы
. С неопределенностью импульса связана неопределенность кинетической энергии частицы
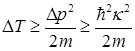 .
.
Используя (1.89), получим
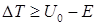 .
.
Таким образом, неопределенность энергии частицы, что локализована в области под барьером, больше той энергии, которой ей не хватает до высоты барьера.
– Конец работы –
Эта тема принадлежит разделу:
Черняков Э.И. Лекции по дисциплине Физические основы электронной техники. Квантовая механика
Черняков Э И Лекции по дисциплине... Физические основы электронной техники Квантовая механика ВВЕДЕНИЕ...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Рассеяние микрочастицы на потенциальной ступени
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов