Волновая функция

Для полного описания состояния системы (частицы) необходимо столько физических величин, сколько степеней свободы имеет система. Совокупность физических величин, которые полностью определяют состояние системы, называетсяполным набором. То есть это наибольшее число независимых величин, которые имеют в данном состоянии определенное значение. Например, для микрочастицы составляющие импульса и 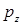будут полным набором.

Как говорилось выше, всякое измерение в квантовой механике изменяет состояние системы. После измерения состояние системы зависит от двух факторов: состояния до измерения и характера измерений.

В некоторых случаях измерение настолько существенно изменяет состояние системы, что после опыта оно зависит только от характера измерения. Такое свойство имеет измерение полного набора физических величин.

После измерения полного набора состояние системы уже не зависит от начального состояния. Возникает новое состояние, в котором полный набор имеет определенное значение. Такие квантовые состояния характеризуются волновой функцией или "пси-функцией" (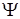- функция).

Волновая функция сама собой физического смысла не имеет (в общем случае она является комплексной величиной), но квадрат ее модуля имеет смысл плотности вероятности.

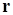Допустим, что система состоит из одной частицы. Эта система характеризуется волновой функцией . Вероятность нахождения частицы в объеме в окрестности точки будет

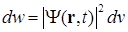. (1.5)

Следовательно, величина 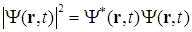является плотностью вероятности. Волновая функция должна подчиняться условиям однозначности, непрерывности (вместе со своими производными), конечности. Кроме того, она должна быть квадратично интегрируемой. Это последнее требование вытекает из условия нормировки волновой функции

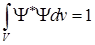. (1.6)

Состояние квантовой системы, в котором физическая величина имеет определенное значение, называется собственными характеризуется собственной волновой функцией. То определенное значение физической величины, которое она имеет в собственном состоянии, называется собственным значением. Совокупность всех собственных значений образует спектр.

Волновая функция свободной микрочастицы имеет вид

, (1.7)

где А – постоянный множитель, который определяется из условия нормировки.