рефераты конспекты курсовые дипломные лекции шпоры

Раздел Механика
/
Вид работы: Лекции
/
Закон сохранения числа микрочастиц

Реферат Курсовая Конспект

Выберите учебное заведение

Закон сохранения числа микрочастиц

Закон сохранения числа микрочастиц - Лекция, раздел Механика, Черняков Э.И. Лекции по дисциплине Физические основы электронной техники. Квантовая механика Получим Из Уравнения Шредингера Закон Сохранения Числа Частиц...

Получим из уравнения Шредингера закон сохранения числа частиц. Запишем уравнение Шредингера и комплексно сопряженное ему

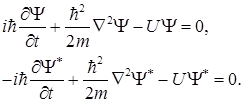
Первое умножим на 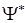, второе на 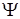и отнимем одно от другого

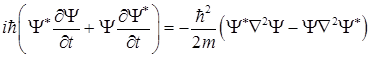Перепишем это выражение таким образом

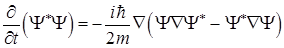. (1.49)

Воспользуемся понятиям вектора плотности потока вероятности 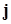(квантовый аналог классического вектора плотности потока частиц) и плотности вероятности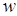

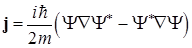, (1.50)

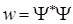. (1.51)

В этом случае из (1.49) получим уравнение непрерывности

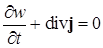. (1.52)

Таким образом, уравнение (1.52) является законом сохранения числа частиц.

Если умножить 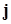на массу частицы 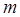, то получим закон сохранения массы

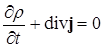, (1.53)

то есть изменение массы в бесконечно малой области обусловлено натеканием или вытеканием этой массы через поверхность, которая ограничивает эту область.

Аналогичное выражение можно получить для закона сохранения заряда, если умножить (1.52) на заряд

, (1.54)

где 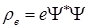, 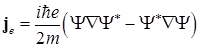. (1.55)

Развернуть

Открыть в широком формате

– Конец работы –

Эта тема принадлежит разделу:

Черняков Э.И. Лекции по дисциплине Физические основы электронной техники. Квантовая механика

Черняков Э И Лекции по дисциплине... Физические основы электронной техники Квантовая механика ВВЕДЕНИЕ...

Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Закон сохранения числа микрочастиц

Что будем делать с полученным материалом:

Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:

Все темы данного раздела:

Волны де Бройля
Квантовая механика является разделом теоретической физики, который изучает движение частиц в области микромира, то есть объясняет явления, которые происходят в объемах с линейными размерами

Измерение в квантовой механике. Соотношение неопределенности
В связи со специфическими особенностями микрообъектов особенного значения приобретает вопрос об измерениях в квантовой механике. Процесс измерения включает в себя наблюдаемую систему, измерительный

Волновая функция
Для полного описания состояния системы (частицы) необходимо столько физических величин, сколько степеней свободы имеет система. Совокупность физических величин, которые полностью определяют сост

Принцип суперпозиции
В классической механике известен принцип суперпозиции. Примером могут служить колебания струны. Наравне с колебаниями чистого типа возможна суперпозиция колебаний различных типов. В

Свободное движение микрочастицы
Рассмотрим некоторые самые простые случаи движения микрочастицы в потенциальных полях. Начнем со свободного движения. Оператор Гамильтона в этом случае имеет вид &

Рассеяние микрочастицы на потенциальной ступени
Потенциальное поле при

Туннельный эффект
Большой интерес вызывает задача прохождения частицы через потенциальный барьер конечной протяжности. Определим коэффициент прозрачности

Микрочастица в потенциальной яме
Сделаем предварительно замечание: непрерывность производной от волновой функции не имеет места, если за некоторой поверхностью потенциальная энергия обращается в бесконечность. В эт

Квантово-механический осциллятор
Атомы в молекулах и кристаллах осуществляют колебания возле положения равновесия. При малых смещениях на атом действует сила, которая пропорциональная смещению

Микрочастица в потенциальной яме конечной глубины
Потенциальное поле ямы имеет вид при

Микрочастица в связанных потенциальных ямах
Задача о движении частицы (электрона) в связанных потенциальных ямах (рис.1.10) оказывается полезной для понимания природы ковалентных связей в молекулах. Решения будем искать в предположе