рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Философия
- /
- Случайные события. Частота. Вероятность.
Реферат Курсовая Конспект
Случайные события. Частота. Вероятность.
Случайные события. Частота. Вероятность. - раздел Философия, ОСНОВНЫЕ ПОНЯТИЯ. Классическое определение вероятности. Теория Вероятностей — Математическая Наука, Изучающая Закономерности Массовых...
Теория вероятностей — математическая наука, изучающая закономерности массовых случайных явлений (событий).
Случайным событием (или просто событием) называется всякое явление, которое может произойти или не произойти при осуществлении определенной совокупности условий. Теория вероятностей имеет дело с такими событиями, которые имеют массовый характер. Это значит, что данная совокупность условий может быть воспроизведена неограниченное число раз. Каждое такое осуществление данной совокупности условий называют испытанием (или опытом).
Если, например, испытание состоит в бросании монеты, то выпадение герба является событием; если испытание — изготовление подшипника данного типа, то соответствие подшипника стандарту — событие; если испытание — бросание игральной кости, т. е. кубика, на гранях которого проставлены цифры (очки) от 1 до 6, to выпадение пятерки — событие.
События будем обозначать заглавными буквами латинского алфавита: A, В, С, ... .
Пусть при n испытаниях событие A появилось m раз.
Отношение m/n называется частотой (относительной частотой) события A и обозначается Р*(А)=m/n
Опыт показывает, что при многократном повторении испытаний частота Р*(А) случайного события обладает устойчивостью. Поясним это на примере.
Пусть при бросании монеты 4040 раз герб выпал 2048 раз. Частота появления герба в данной серии опытов равна Р*(А)=m/n=2048/4040=0,5069. При бросании той же монеты 12000 раз герб выпал 6019 раз. Следовательно, в этом случае частота Р*(А)=6019/12000=0,5016. Наконец, при 24000 бросаний герб появился 12012 раз с частотой Р*(А)=0,5005. Таким образом, мы видим, что при большом числе бросаний монеты частота появления герба обладает устойчивостью, т. е. мало отличается от числа 0,5. Как показывает опыт, это отклонение частоты от числа 0,5 уменьшается с увеличением числа испытаний. Наблюдаемое в этом примере свойство устойчивости частоты является общим свойством массовых случайных событий, а именно, всегда существует такое число, к которому приближается частота появления данного события, мало отличаясь от него при большом числе испытаний. Это число называетсявероятностью события. Оно выражает объективную возможность появления события. Чем больше вероятность события, тем более возможным оказывается его появление. Вероятность события A будем обозначать через Р(А). В рассмотренном выше примере вероятность появления герба, очевидно, равна 0,5.
Событие называется достоверным, если оно в данном опыте обязательно должно произойти; наоборот, событие называетсяневозможным, если оно в данном опыте не может произойти.
Пусть, например, из урны, содержащей только черные шары, вынимают шар. Тогда появление черного шара — достоверное событие; появление белого шара — невозможное событие.
Если событие достоверно, то оно произойдет при каждом испытании (m=n). Поэтому частота достоверного события всегда равна единице. Наоборот, если событие невозможно, то оно ни при одном испытании не осуществится (m=0). Следовательно, частота невозможного события в любой серии испытаний равна нулю. Поэтому вероятность достоверного события равна единице, а вероятность невозможного события равна нулю.
Если событие A не является ни достоверным, ни невозможным, то его частота m/n при большом числе испытаний будет мало отличаться от некоторого числа p (где 0 < p < 1 ) — вероятности события A.
Совмещением (или произведением) двух событий A и В называется событие, состоящее в совместном наступлении как события A, так и события В. Это событие будем обозначать АВ или ВА.
Аналогично, совмещением нескольких событий, например A, В и С, называется событие D=ABC, состоящее в совместном наступлении событий A, В и С.
Объединением (или суммой) двух событий A и В называется событие С, заключающееся в том, что произойдет по крайней мере одно из событий A или В. Это событие обозначается так: С=А+В.
Объединением нескольких событий называется событие, состоящее в появлении по крайней мере одного из них. Запись D=A+B+Cозначает, что событие D есть объединение событий A, В и С.
Два события A и В называются несовместными, если наступление события A исключает наступление события В. Отсюда следует, что если события A и В несовместны, то событие AB — невозможное.
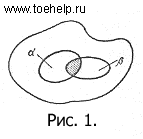
Рассмотрим следующий пример. Будем следить за движением какой-нибудь определенной молекулы газа, заключенного в некоторый объем. Внутри этого объема выделим объемы 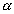 и и 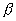 , частично перекрывающие друг друга (рис. 1). Пусть событие A — попадание молекулы в объем , частично перекрывающие друг друга (рис. 1). Пусть событие A — попадание молекулы в объем 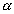 , событие В — попадание молекулы в объем , событие В — попадание молекулы в объем 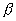 . Совмещением событий A и В является попадание молекулы в общую часть объемов . Совмещением событий A и В является попадание молекулы в общую часть объемов 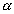 и и 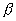 . Если объемы . Если объемы 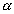 и и 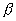 не имеют общих точек, то ясно, что события A и В несовместны. Объединением событий A и В является попадание молекулы или только в объем не имеют общих точек, то ясно, что события A и В несовместны. Объединением событий A и В является попадание молекулы или только в объем 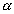 или только в объем или только в объем 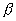 , или же в их общую часть. , или же в их общую часть.
| 
|
2. Аксиомы вероятностей.
Пусть A и B — два несовместных события, причем в n испытаниях событие A произошло m1 раз, а событие В произошло m2 раз. Тогда частоты событий A и В соответственно равны P*(A)=m1/n, P*(B)=m2/n. Так как события A и В несовместны, то событие A+B в данной серии опытов произошло m1+m2 раз. Следовательно,

Таким образом, частота события A+B равна сумме частот событий A и В. Но при больших n частоты P*(A), P*(B) и P*(A+B) мало отличаются от соответствующих вероятностей P(A), P(B) и P(A+B). Поэтому естественно принять, что если A и В — несовместные события, то P(A+B)=P(A)+P(B)
Изложенное позволяет высказать следующие свойства вероятностей, которые мы принимаем в качестве аксиом.
Аксиома 1. Каждому случайному событию A соответствует определенное число Р(А), называемое его вероятностью и удовлетворяющее условию  .
.
Аксиома 2. Вероятность достоверного события равна единице.
Аксиома 3 (аксиома сложения вероятностей). Пусть A и В — несовместные события. Тогда вероятность того, что произойдет хотя бы одно из этих двух событий, равна сумме их вероятностей:
| P(A+B)=P(A)+P(B) | (1) |
Аксиома 3 допускает обобщение на случай нескольких событий, а именно: если события A1, A2, ..., An, попарно несовместны, то

| (2) |
Событием, противоположным событию 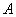 , называется событие
, называется событие 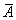 , состоящее в ненаступлении события
, состоящее в ненаступлении события 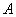 . Очевидно, события
. Очевидно, события 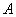 и
и 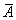 несовместны.
несовместны.
Пусть, например, событие 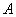 состоит в том, что изделие удовлетворяет стандарту; тогда противоположное событие
состоит в том, что изделие удовлетворяет стандарту; тогда противоположное событие 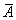 заключается в том, что изделие стандарту не удовлетворяет. Пусть событие
заключается в том, что изделие стандарту не удовлетворяет. Пусть событие 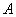 — выпадение четного числа очков при однократном бросании игральной кости; тогда
— выпадение четного числа очков при однократном бросании игральной кости; тогда 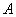 — выпадение нечетного числа очков.
— выпадение нечетного числа очков.
Теорема 1. Для любого события 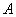 вероятность противоположного события
вероятность противоположного события 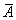 выражается равенством
выражается равенством
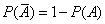
| (3) |
Доказательство. Событие 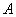 +
+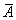 , состоящее в наступлении или события
, состоящее в наступлении или события 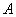 , или события
, или события 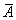 , очевидно, является достоверным. Поэтому на основании аксиомы 2 имеем Р(
, очевидно, является достоверным. Поэтому на основании аксиомы 2 имеем Р(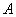 +
+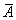 )=1. Так как события
)=1. Так как события 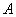 и
и 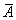 несовместны, то используя аксиому 3, получим Р(
несовместны, то используя аксиому 3, получим Р(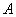 +
+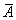 )=Р(
)=Р(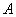 )+P(
)+P(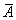 ). Следовательно, Р(
). Следовательно, Р(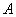 )+P(
)+P(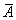 )=1, откуда
)=1, откуда 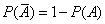 .
.
Теорема 2. Вероятность невозможного события равна нулю.
Доказательство непосредственно следует из аксиомы 2 и теоремы 1, если заметить, что невозможное событие противоположно достоверному событию.
– Конец работы –
Эта тема принадлежит разделу:
ОСНОВНЫЕ ПОНЯТИЯ. Классическое определение вероятности.
Классическое определение вероятности... Как было сказано выше при большом числе n испытаний частота P A m n... Это обстоятельство позволяет находить приближенно вероятность события опытным путем Практически такой способ...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Случайные события. Частота. Вероятность.
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов