рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Философия
- /
- Дискретные случайные величины.
Реферат Курсовая Конспект
Дискретные случайные величины.
Дискретные случайные величины. - раздел Философия, ОСНОВНЫЕ ПОНЯТИЯ. Классическое определение вероятности. Рассмотрим Случайную Величину * ...
Рассмотрим случайную величину *  , возможные значения которой образуют конечную или бесконечную последовательность чисел x1, x2, ..., xn, ... . Пусть задана функция p(x), значение которой в каждой точке x=xi (i=1,2, ...) равно вероятности того, что величина
, возможные значения которой образуют конечную или бесконечную последовательность чисел x1, x2, ..., xn, ... . Пусть задана функция p(x), значение которой в каждой точке x=xi (i=1,2, ...) равно вероятности того, что величина  примет значение xi
примет значение xi
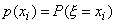
| (16) |
Такая случайная величина  называется дискретной (прерывной). Функция р(х) называется законом распределения вероятностей случайной величины, или кратко, законом распределения. Эта функция определена в точках последовательности x1, x2, ..., xn, ... . Так как в каждом из испытаний случайная величина
называется дискретной (прерывной). Функция р(х) называется законом распределения вероятностей случайной величины, или кратко, законом распределения. Эта функция определена в точках последовательности x1, x2, ..., xn, ... . Так как в каждом из испытаний случайная величина  принимает всегда какое-либо значение из области ее изменения, то
принимает всегда какое-либо значение из области ее изменения, то
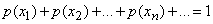
Пример 1. Случайная величина  — число очков, выпадающих при однократном бросании игральной кости. Возможные значения
— число очков, выпадающих при однократном бросании игральной кости. Возможные значения  — числа 1, 2, 3, 4, 5 и 6. При этом вероятность того, что
— числа 1, 2, 3, 4, 5 и 6. При этом вероятность того, что  примет любое из этих значений, одна и та же и равна 1/6. Какой будет закон распределения ?
примет любое из этих значений, одна и та же и равна 1/6. Какой будет закон распределения ?
Решение: Таким образом, здесь закон распределения вероятностей есть функция р(х)=1/6 для любого значения х из множества {1, 2, 3, 4, 5, 6}.
Пример 2. Пусть случайная величина  - число наступления события A при одном испытании, причем P(A)=p. Множество возможных значений
- число наступления события A при одном испытании, причем P(A)=p. Множество возможных значений  состоит из 2-х чисел 0 и 1:
состоит из 2-х чисел 0 и 1:  =0, если событие A не произошло, и
=0, если событие A не произошло, и  =1, если событие A произошло. Таким образом,
=1, если событие A произошло. Таким образом,
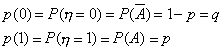
Предположим, что производится n независимых испытаний, в результате каждого из которых может наступить или не наступить событиеA. Пусть вероятность наступления события A при каждом испытании равна p. Рассмотрим случайную величину  — число наступлений события A при n независимых испытаниях. Область изменения
— число наступлений события A при n независимых испытаниях. Область изменения  состоит из всех целых чисел от 0 до n включительно. Закон распределения вероятностей р(m) определяется формулой Бернулли (13'):
состоит из всех целых чисел от 0 до n включительно. Закон распределения вероятностей р(m) определяется формулой Бернулли (13'):

Закон распределения вероятностей по формуле Бернулли часто называют биномиальным, так как Pn(m) представляет собой m-й член разложения бинома 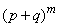 .
.
Пусть случайная величина  может принимать любое целое неотрицательное значение, причем
может принимать любое целое неотрицательное значение, причем
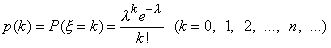
| (17) |
где 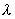 — некоторая положительная постоянная. В этом случае говорят, что случайная величина
— некоторая положительная постоянная. В этом случае говорят, что случайная величина  распределена по закону Пуассона, Заметим, что при k=0 следует положить 0!=1.
распределена по закону Пуассона, Заметим, что при k=0 следует положить 0!=1.
Как мы знаем, при больших значениях числа n независимых испытаний вероятность Pn(m) наступления m раз события A удобнее находить не по формуле Бернулли, а по формуле Лапласа [см. формулу (15)]. Однако последняя дает большие погрешности при малой вероятности р появления события А в одном испытании. В этом случае для подсчета вероятности Pn(m) удобно пользоваться формулой Пуассона, в которой следует положить 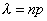 .
.
Формулу Пуассона можно получить как предельный случай формулы Бернулли при неограниченном увеличении числа испытаний n и при стремлении к нулю вероятности  .
.
Пример 3. На завод прибыла партия деталей в количестве 1000 шт. Вероятность того, что деталь окажется бракованной, равна 0,001. Какова вероятность того, что среди прибывших деталей будет 5 бракованных?
Решение:
Здесь 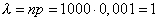 .
.
По формуле (17) находим
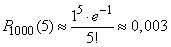
Распределение Пуассона часто встречается и в других задачах. Так, например, если телефонистка в среднем за один час получает Nвызовов, то, как можно показать, вероятность Р(k) того, что в течение одной минуты она получит k вызовов, выражается формулой Пуассона, если положить  .
.
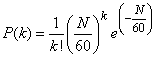
Если возможные значения случайной величины  образуют конечную последовательность x1, x2, ..., xn, то закон распределения вероятностей случайной величины задают в виде следующей таблицы, в которой
образуют конечную последовательность x1, x2, ..., xn, то закон распределения вероятностей случайной величины задают в виде следующей таблицы, в которой
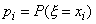
и
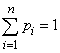
Значения 
| x1 | x2 | ... | xn |
| Вероятности p(xi) | p1 | p2 | ... | pn |
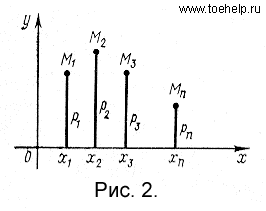
Эту таблицу называют рядом распределения случайной величины  . Наглядно функцию р(х) можно изобразить в виде графика. Для этого возьмем прямоугольную систему координат на плоскости.
. Наглядно функцию р(х) можно изобразить в виде графика. Для этого возьмем прямоугольную систему координат на плоскости.
По горизонтальной оси будем откладывать возможные значения случайной величины  , а по вертикальной оси - значения функции
, а по вертикальной оси - значения функции 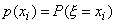 . График функции р(х) изображен на рис. 2. Если соединить точки этого графика прямолинейными отрезками, то получится фигура, которая называется многоугольником распределения.
. График функции р(х) изображен на рис. 2. Если соединить точки этого графика прямолинейными отрезками, то получится фигура, которая называется многоугольником распределения.
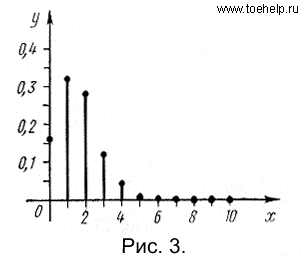
Пример 4. Пусть событие А — появление одного очка при бросании игральной кости; Р(A)=1/6. Рассмотрим случайную величину  — число наступлений события А при десяти бросаниях игральной кости. Значения функции р(х) (закона распределения) приведены в следующей таблице:
— число наступлений события А при десяти бросаниях игральной кости. Значения функции р(х) (закона распределения) приведены в следующей таблице:
Значения 
| |||||||||||
| Вероятности p(xi) | 0,162 | 0,323 | 0,291 | 0,155 | 0,054 | 0,013 | 0,002 |
Вероятности p(xi) вычислены по формуле Бернулли при n=10. Для x>6 они практически равны нулю. График функции p(x) изображен на рис. 3.
Дальше...
* Случайные величины будем обозначать малыми буквами греческого алфавита: 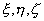 , ... .
, ... .
– Конец работы –
Эта тема принадлежит разделу:
ОСНОВНЫЕ ПОНЯТИЯ. Классическое определение вероятности.
Классическое определение вероятности... Как было сказано выше при большом числе n испытаний частота P A m n... Это обстоятельство позволяет находить приближенно вероятность события опытным путем Практически такой способ...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Дискретные случайные величины.
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов