рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Философия
- /
- Образец решения контрольной работы № 2.
Реферат Курсовая Конспект
Образец решения контрольной работы № 2.
Образец решения контрольной работы № 2. - раздел Философия, Часть 1. ПРОГРАММА КУРСА Элементы векторной алгебры и аналитической геометрии. Задание 1. Найти Пределы Функций. 1) ...
Задание 1. Найти пределы функций.
1) 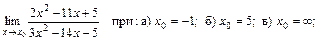
2) 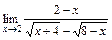 ; 3)
; 3)  .
.
Решение. 1) Данный предел в зависимости от значений 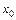 вычисляется разными способами.
вычисляется разными способами.
а) 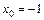 . Найдем значения функций, стоящих в числителе и в знаменателе дроби,
. Найдем значения функций, стоящих в числителе и в знаменателе дроби,  в точке
в точке 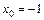 :
: 
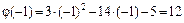 . Так как полученные значения конечны и отличны от нуля, то по теореме о пределе частного, учитывая непрерывность функций, предел равен значению частного в предельной точке:
. Так как полученные значения конечны и отличны от нуля, то по теореме о пределе частного, учитывая непрерывность функций, предел равен значению частного в предельной точке:  ;
;
б) 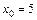 . Найдем новые значения
. Найдем новые значения  и
и 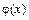 в точке
в точке 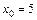 :
: 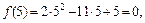
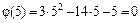 . Так как числитель и знаменатель дроби оба равны нулю, то заданное отношение в точке
. Так как числитель и знаменатель дроби оба равны нулю, то заданное отношение в точке 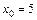 является неопределенностью вида
является неопределенностью вида  и применять теорему о пределе частного нельзя. Для нахождения предела в этом случае выделим в числителе и знаменателе критический множитель
и применять теорему о пределе частного нельзя. Для нахождения предела в этом случае выделим в числителе и знаменателе критический множитель  , создающий неопределенность вида
, создающий неопределенность вида  при
при 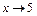 . С этой целью найдем корни уравнений
. С этой целью найдем корни уравнений 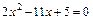 и
и 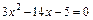 , затем разложим квадратные трехчлены на линейные множители и после сокращения дроби на общий критический множитель
, затем разложим квадратные трехчлены на линейные множители и после сокращения дроби на общий критический множитель  найдем предел оставшегося выражения, применяя теорему о пределе частного как в случае пункта а):
найдем предел оставшегося выражения, применяя теорему о пределе частного как в случае пункта а):
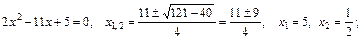
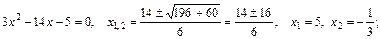
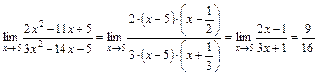 ;
;
в)  . При
. При 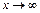 имеем
имеем 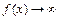 и
и 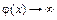 , т. е. заданное отношение при
, т. е. заданное отношение при 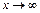 является неопределенностью вида
является неопределенностью вида  и теорему о пределе частного применять нельзя. Для нахождения в этом случае предела дроби опять выделим в числителе и знаменателе критический множитель, который представляет собой старшую степень переменной
и теорему о пределе частного применять нельзя. Для нахождения в этом случае предела дроби опять выделим в числителе и знаменателе критический множитель, который представляет собой старшую степень переменной  . В данном случае это есть
. В данном случае это есть 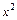 . После сокращения дроби на критический множитель
. После сокращения дроби на критический множитель 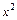 применим теорему о пределе частного и следующие равенства, известные из теории пределов:
применим теорему о пределе частного и следующие равенства, известные из теории пределов:  ,
, 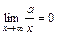 ,
, 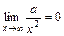 .
.
Получим:
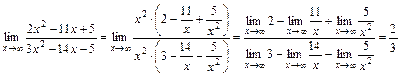 .
.
2) Найдем значения функций 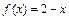 и
и 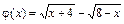 , стоящих в числителе и знаменателе дроби, в точке
, стоящих в числителе и знаменателе дроби, в точке  :
: 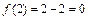 ,
,  . Следовательно, заданное отношение
. Следовательно, заданное отношение 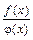 при
при 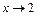 является неопределенностью вида
является неопределенностью вида  . Для нахождения предела отношения выделим в числителе и в знаменателе критический множитель
. Для нахождения предела отношения выделим в числителе и в знаменателе критический множитель 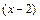 , создающий неопределенность, и сократим на него дробь. С этой целью умножим числитель и знаменатель на выражение сопряженное знаменателю
, создающий неопределенность, и сократим на него дробь. С этой целью умножим числитель и знаменатель на выражение сопряженное знаменателю 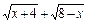 и используем формулу сокращенного умножения разности квадратов:
и используем формулу сокращенного умножения разности квадратов: 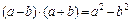 :
:


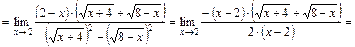
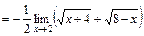 .
.
По теореме о пределе корня 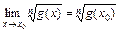 , получим:
, получим:
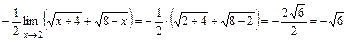 .
.
3) 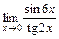 . Найдем значения функций
. Найдем значения функций 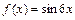 и
и 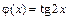 в точке
в точке 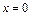 :
:  и
и 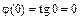 . Следовательно, заданное отношение представляет собой при
. Следовательно, заданное отношение представляет собой при 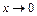 неопределенность вида
неопределенность вида  . Вычислим этот предел, применяя формулу первого замечательного предела:
. Вычислим этот предел, применяя формулу первого замечательного предела: 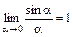 и равенство
и равенство 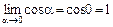 , вытекающее из непрерывности в точке
, вытекающее из непрерывности в точке 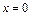 функции
функции  . С этой целью преобразуем заданный предел следующим образом:
. С этой целью преобразуем заданный предел следующим образом:
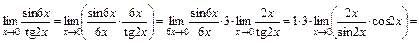
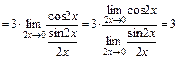 .
.
Ответ: 1), а)  ; б)
; б)  ; в)
; в)  . 2)
. 2)  . 3) 3.
. 3) 3.
Задание 2. Найти производные заданных функций.
1) 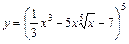 ; 2)
; 2) 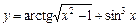 ;
;
3)  .
.
Решение. 1) 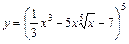 .
.
Используем правило дифференцирование суммы 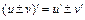 и правила дифференцирования сложной функции вида
и правила дифференцирования сложной функции вида  , где
, где 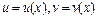 , а также таблицу производных. Получим:
, а также таблицу производных. Получим:
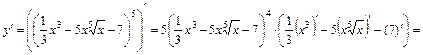
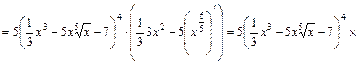
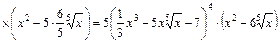 .
.
2) 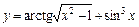 .
.
Используем правило дифференцирование суммы 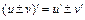 и правила дифференцирования сложных функций вида
и правила дифференцирования сложных функций вида
 ,
,
где 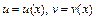 , а также таблицу производных. Получим:
, а также таблицу производных. Получим:

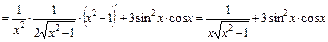 .
.
3)  .
.
Используем правило дифференцирования суммы 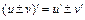 , правило дифференцирования произведения
, правило дифференцирования произведения 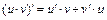 и правила дифференцирования сложных функций вида
и правила дифференцирования сложных функций вида
 ,
,
где 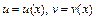 , а также таблицу производных. Получим:
, а также таблицу производных. Получим:
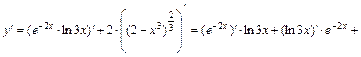
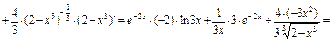
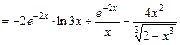 .
.
Ответ: 1) 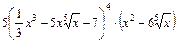 ; 2)
; 2) 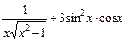 ; 3)
; 3) 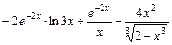 .
.
Задание 3. Провести полное исследование функции 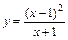 и построить ее график.
и построить ее график.
Решение. 1) Найдем область определения, интервалы непрерывности и точки разрыва функции.
Функция определена на всей числовой оси, кроме точки  , т. е.
, т. е. 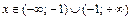 . В каждой точке области определения функция непрерывна. Точка
. В каждой точке области определения функция непрерывна. Точка  есть точка разрыва функции, т. к. знаменатель функции в этой точке равен нулю, а числитель отличен от нуля.
есть точка разрыва функции, т. к. знаменатель функции в этой точке равен нулю, а числитель отличен от нуля.
2) Выясним четность, нечетность и периодичность функции.
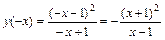 , т. е.
, т. е.  . Следовательно, функция не является ни четной, ни нечетной.
. Следовательно, функция не является ни четной, ни нечетной.
Функция непериодична, т. к. 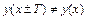 , где Т – некоторое действительное число.
, где Т – некоторое действительное число.
3) Найдем асимптоты графика функции (вертикальные, горизонтальные и наклонные).
|
Так как точка  оси Ox есть точка разрыва функции, то прямая линия
оси Ox есть точка разрыва функции, то прямая линия  , перпендикулярная оси Ox, есть вертикальная асимптота графика. Исследуем поведение графика функции вблизи вертикальной асимптоты по односторонним пределам функции. Возьмем слева от точки
, перпендикулярная оси Ox, есть вертикальная асимптота графика. Исследуем поведение графика функции вблизи вертикальной асимптоты по односторонним пределам функции. Возьмем слева от точки  близкое значение, например,
близкое значение, например, 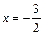 и вычислим в нем значение функции и ее знак:
и вычислим в нем значение функции и ее знак:
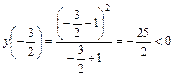 .
.
Так как это значение отрицательно, и функция слева от точки  непрерывна, то она сохраняет знак и
непрерывна, то она сохраняет знак и  .
.
Теперь возьмем справа от точки  близкое значение, например,
близкое значение, например, 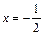 :
:
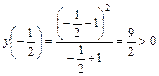 .
.
Так как это значение положительно, и функция справа от точки  непрерывна, то при переходе к пределу функция сохраняет знак и
непрерывна, то при переходе к пределу функция сохраняет знак и 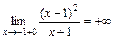 .
.
Таким образом, слева от точки  функция отрицательна, а справа от точки
функция отрицательна, а справа от точки  – положительна и имеет односторонние пределы, равные бесконечности. Такая точка называется точкой разрыва второго рода (или точкой бесконечного разрыва функции).
– положительна и имеет односторонние пределы, равные бесконечности. Такая точка называется точкой разрыва второго рода (или точкой бесконечного разрыва функции).
б) Горизонтальные асимптоты.
Для нахождения горизонтальной асимптоты нужно найти предел функции при 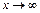 , раскрывая неопределенность вида
, раскрывая неопределенность вида  . Если существует конечный предел
. Если существует конечный предел  , то прямая, определяемая уравнением
, то прямая, определяемая уравнением 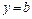 , есть горизонтальная асимптота графика. Если же этот предел равен бесконечности, то горизонтальной асимптоты нет. Найдем предел:
, есть горизонтальная асимптота графика. Если же этот предел равен бесконечности, то горизонтальной асимптоты нет. Найдем предел:
 .
.
Предел равен бесконечности, значит горизонтальной асимптоты нет.
в) Наклонные асимптоты.
Наклонная асимптота имеет уравнение прямой линии с угловым коэффициентом вида 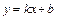 , где
, где 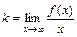 ,
, 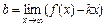 . Если
. Если 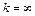 , то наклонной асимптоты не существует.
, то наклонной асимптоты не существует.
Найдем оба указанных предела для заданной функции:
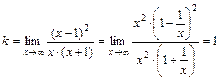 ,
,
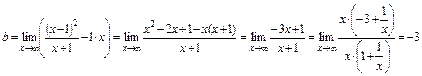 .
.
Таким образом, график имеет наклонную асимптоту 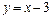 .
.
4) Найдем интервалы возрастания и убывания функции, точки экстремума и экстремумы функции.
Находим сначала первую производную функции:
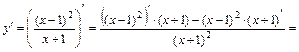
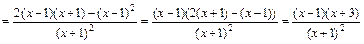 .
.
Так как точка  , в которой
, в которой 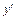 не существует, не принадлежит области определения функции, то критическими точками первого рода являются лишь точки, в которых
не существует, не принадлежит области определения функции, то критическими точками первого рода являются лишь точки, в которых 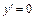 или
или  , т. е.
, т. е.  .
.
Критические точки и точка разрыва  разбивают ось Ox на 4 интервала монотонности функции. По знаку производной
разбивают ось Ox на 4 интервала монотонности функции. По знаку производной 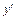 в этих интервалах определяем интервалы возрастания и убывания функции, точки экстремума и экстремумы функции. Полученные данные заносим в табл. 1.
в этих интервалах определяем интервалы возрастания и убывания функции, точки экстремума и экстремумы функции. Полученные данные заносим в табл. 1.
Таблица 1.

| 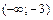
| 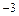
| 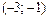
| 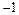
| 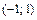
| 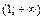
| |
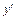
| + | – | не сущ. | – | + | ||

| ä | –8 max | æ | не сущ. | æ | min | ä |
5) Найдем интервалы выпуклости и вогнутости графика функции, точки перегиба.
Находим сначала вторую производную функции:
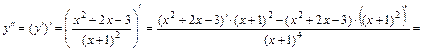

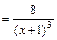 .
.
Так как точка не принадлежит области определения функции и
не принадлежит области определения функции и 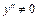 , то критических точек второго рода нет.
, то критических точек второго рода нет.
Точка разрыва разбивают числовую ось Ox на 2 интервала, в которых по знаку второй производной 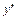 определяем интервалы выпуклости и вогнутости графика. Полученные данные заносим в табл. 2.
определяем интервалы выпуклости и вогнутости графика. Полученные данные заносим в табл. 2.
Таблица 2.

| 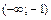
| 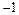
| 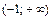
|
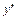
| – | не сущ. | + |

| Ç выпуклый | не сущ. | È вогнутый |
6) Находим точки пересечения графика функции с осями координат, решая две системы уравнений.
С осью Ox:
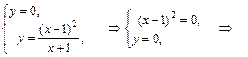 А(1; 0) – точка пересечения графика с осью Ox.
А(1; 0) – точка пересечения графика с осью Ox.
С осью Oy:
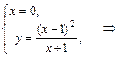 В(0; 1) – точка пересечения графика с осью Oу.
В(0; 1) – точка пересечения графика с осью Oу.
7) Используя результаты исследования, строим график функции в такой последовательности: а) рисуем вертикальную асимптоту  и наклонную асимптоту
и наклонную асимптоту 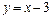 , подписываем их; б) изображаем максимум функции в точке
, подписываем их; б) изображаем максимум функции в точке 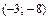 и минимум в точке
и минимум в точке  ; в) наносим на осях точки А(1; 0) и В(0; 1) пересечения графика с осями координат; г) нанесенные на плоскость точки соединяем гладкими линиями с учетом табл. 1 и 2 и поведения функции вблизи асимптот.
; в) наносим на осях точки А(1; 0) и В(0; 1) пересечения графика с осями координат; г) нанесенные на плоскость точки соединяем гладкими линиями с учетом табл. 1 и 2 и поведения функции вблизи асимптот.
 |
Задание 4. Доказать, что функция 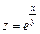 удовлетворяет уравнению
удовлетворяет уравнению 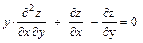 .
.
Решение. По определению частной производной находим 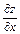 , считая переменную y фиксированной постоянной величиной:
, считая переменную y фиксированной постоянной величиной:

Аналогично находим частную производную 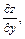 считая переменную x фиксированной постоянной величиной:
считая переменную x фиксированной постоянной величиной:
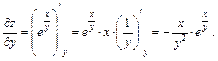
Находим смешанную частную производную 2-го порядка, используя правило дифференцирования произведения двух функций:

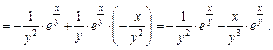
Подставляем найденные частные производные в данное уравнение:
 .
.
Ответ: что и требовалось доказать.
3.1. Контрольная работа № 3. «Интегральное исчисление».
1. Найти неопределенные интегралы. Результаты проверить дифференцированием.
1. 1)  ; 2)
; 2)  ;
;
3) 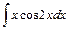 ; 4)
; 4) 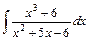 .
.
2. 1) 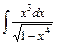 ; 2)
; 2) 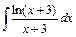 ;
;
3)  ; 4)
; 4)  .
.
3. 1) 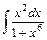 ; 2)
; 2) 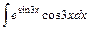 ;
;
3) 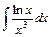 ; 4)
; 4) 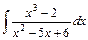 .
.
4. 1)  ; 2)
; 2) 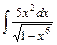 ;
;
3) 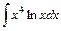 ; 4)
; 4) 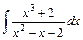 .
.
5. 1) 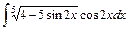 ; 2)
; 2) 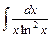 ;
;
3) 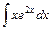 ; 4)
; 4) 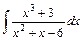 .
.
6. 1)  ; 2)
; 2) 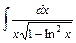 ;
;
3) 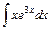 ; 4)
; 4)  .
.
7. 1) 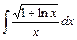 ; 2)
; 2) 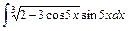 ;
;
3) 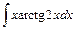 ; 4)
; 4) 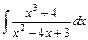 .
.
8. 1) 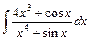 ; 2)
; 2) 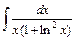 ;
;
3) 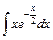 ; 4)
; 4) 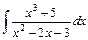 .
.
9. 1) 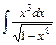 ; 2)
; 2)  ;
;
3) 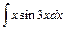 ; 4)
; 4)  .
.
10. 1) 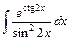 ; 2)
; 2)  ;
;
3) 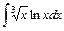 ; 4)
; 4) 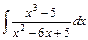 .
.
2. Вычислить по формуле Ньютона-Лейбница определенный интеграл.
1. 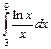 . 2.
. 2. 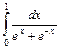 . 3.
. 3. 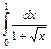 .
.
4. 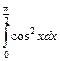 . 5.
. 5. 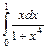 . 6.
. 6. 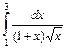 .
.
7. 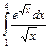 . 8.
. 8. 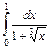 . 9.
. 9. 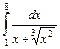 .
.
10. 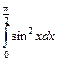 .
.
3. Вычислить площадь фигуры, ограниченной графиками функций. Сделать чертеж.
1. 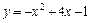 ,
, 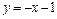 . 2.
. 2. 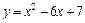 ,
, 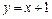 .
.
3.  ,
, 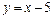 . 4.
. 4. 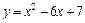 ,
, 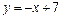 .
.
5.  ,
, 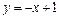 . 6.
. 6.  ,
,  .
.
7. 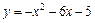 ,
, 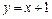 . 8.
. 8.  ,
, 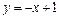 .
.
9. 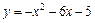 ,
, 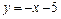 . 10.
. 10. 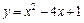 ,
, 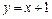 .
.
4. Вычислить объем тела, образованного вращением вокруг оси Ох фигуры, ограниченной графиками функций.
1. 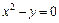 ,
, 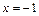 ,
,  . 2.
. 2. 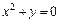 ,
,  ,
, 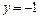 .
.
3. 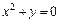 ,
, 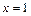 ,
,  . 4.
. 4. 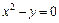 ,
,  ,
, 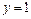 .
.
5. 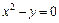 ,
, 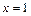 ,
,  . 6.
. 6.  ,
, 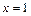 ,
,  .
.
7.  ,
,  ,
, 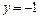 . 8.
. 8.  ,
, 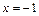 ,
,  .
.
9.  ,
,  ,
, 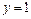 . 10.
. 10.  ,
,  ,
, 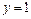 .
.
– Конец работы –
Эта тема принадлежит разделу:
Часть 1. ПРОГРАММА КУРСА Элементы векторной алгебры и аналитической геометрии.
Волгоградский государственный архитектурно строительный университет... Волжский институт строительства и технологий...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Образец решения контрольной работы № 2.
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов