рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Философия
- /
- Образец решения контрольной работы № 4.
Реферат Курсовая Конспект
Образец решения контрольной работы № 4.
Образец решения контрольной работы № 4. - раздел Философия, Часть 1. ПРОГРАММА КУРСА Элементы векторной алгебры и аналитической геометрии. Задание 1. Найти Общее Решение Линейного Дифференциального У...
Задание 1. Найти общее решение линейного дифференциального уравнения первого порядка 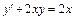 и частное решение, удовлетворяющее начальному условию y(0) = 0.
и частное решение, удовлетворяющее начальному условию y(0) = 0.
Решение. Общее решение будем искать методом Бернулли: 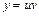 , где
, где 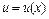 ,
,  – две новые неизвестные функции, тогда
– две новые неизвестные функции, тогда 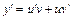 . Подставляя в исходное уравнение, получаем
. Подставляя в исходное уравнение, получаем  или
или  . Подберем функцию v так, чтобы выражение в скобках было равно нулю, тогда получим
. Подберем функцию v так, чтобы выражение в скобках было равно нулю, тогда получим  Найдем частное решение уравнения (I) при С1 = 0, которое является ДУ с разделяющимися переменными. Для этого в этом уравнении разделим переменные x и y:
Найдем частное решение уравнения (I) при С1 = 0, которое является ДУ с разделяющимися переменными. Для этого в этом уравнении разделим переменные x и y: 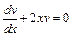 или
или 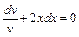 . Проинтегрировав обе части, получим
. Проинтегрировав обе части, получим 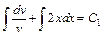 или
или 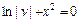 (при С1= 0) или
(при С1= 0) или 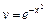 – частное решение уравнения (I). Подставляя полученную функцию v в уравнение (II), получаем тоже ДУ с разделяющимися переменными:
– частное решение уравнения (I). Подставляя полученную функцию v в уравнение (II), получаем тоже ДУ с разделяющимися переменными:  , для которого найдем его общее решение. Разделяем переменные:
, для которого найдем его общее решение. Разделяем переменные: 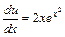 или
или 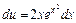 . Интегрируем обе части:
. Интегрируем обе части: 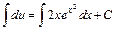 или
или  – общее решение уравнения
– общее решение уравнения  . Таким образом
. Таким образом 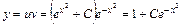 – общее решение исходного уравнения.
– общее решение исходного уравнения.
Для нахождения частного решения исходного уравнения, удовлетворяющего начальному условию y(0) = 0 подставим в найденное общее решение x = 0 и y = 0 и найдем постоянную С:  или
или 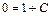 , т. е. С = –1. Таким образом,
, т. е. С = –1. Таким образом, 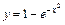 – частное решение исходного уравнения при y(0) = 0.
– частное решение исходного уравнения при y(0) = 0.
Ответ:  – общее решение;
– общее решение; 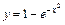 – частное решение.
– частное решение.
Задание 2. Найти общее решение линейного неоднородного дифференциального уравнения 2-го порядка с постоянными коэффициентами с правой частью специального вида и частное решение, удовлетворяющее начальным условиям y(x0) = y0 и 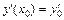
1) 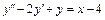 , y(0) = –1,
, y(0) = –1, 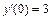 ;
;
2)  , y(0) = 1,
, y(0) = 1,  ;
;
3)  , y(0) = 2,
, y(0) = 2, 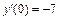 .
.
Решение. Общее решение линейного неоднородного дифференциального уравнения 2-го порядка с постоянными коэффициентами с правой частью специального вида будем искать в виде  , где
, где 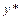 – общее решение соответствующего линейного однородного ДУ 2-го порядка с постоянными коэффициентами, а
– общее решение соответствующего линейного однородного ДУ 2-го порядка с постоянными коэффициентами, а  – некоторое частное решение исходного уравнения.
– некоторое частное решение исходного уравнения.
1) Найдем общее решение 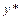 соответствующего линейного однородного ДУ 2-го порядка с постоянными коэффициентами
соответствующего линейного однородного ДУ 2-го порядка с постоянными коэффициентами  . Характеристическое уравнение
. Характеристическое уравнение 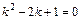 имеет два равных корня
имеет два равных корня  , значит
, значит 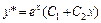 .
.
Найдем частное решение  исходного уравнения. В нем правая часть
исходного уравнения. В нем правая часть 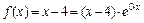 есть формула вида
есть формула вида  , причем n = 1 и a = 0 – не корень характеристического уравнения. Поэтому частное решение
, причем n = 1 и a = 0 – не корень характеристического уравнения. Поэтому частное решение  , где А и В – неопределенные коэффициенты. Тогда
, где А и В – неопределенные коэффициенты. Тогда 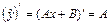 и
и 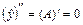 . Подставив
. Подставив  ,
, 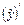 ,
, 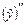 в исходное уравнение, получим –2А + Ax + B = x – 4 или Ax + (–2А + B) = x – 4. Приравнивая коэффициенты при одинаковых степенях x, получаем систему уравнений
в исходное уравнение, получим –2А + Ax + B = x – 4 или Ax + (–2А + B) = x – 4. Приравнивая коэффициенты при одинаковых степенях x, получаем систему уравнений  Отсюда A = 1, B = –2. Поэтому частное решение исходного уравнения имеет вид
Отсюда A = 1, B = –2. Поэтому частное решение исходного уравнения имеет вид  . Следовательно,
. Следовательно, 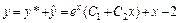 – общее решение исходного уравнения.
– общее решение исходного уравнения.
Для нахождения частного решения исходного уравнения, удовлетворяющего начальным условиям y(0) = –1, 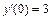 найдем
найдем 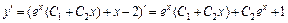 . Подставим начальные условия в найденное общее решение и его производную, получим систему
. Подставим начальные условия в найденное общее решение и его производную, получим систему  или
или 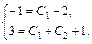 Отсюда С1 = С2 = 1. Таким образом, искомое частное решение имеет вид:
Отсюда С1 = С2 = 1. Таким образом, искомое частное решение имеет вид: 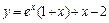 .
.
2) Найдем общее решение 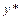 соответствующего однородного уравнения
соответствующего однородного уравнения  . Составим характеристическое уравнение
. Составим характеристическое уравнение 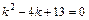 , дискриминант
, дискриминант 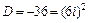 , имеет два комплексных корня
, имеет два комплексных корня  ,
, 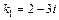 . Следовательно,
. Следовательно,  .
.
Найдем частное решение  исходного уравнения. Его правая часть
исходного уравнения. Его правая часть  есть формула вида
есть формула вида  , причем n = m = 0, a = 0, b = 3. Так как числа
, причем n = m = 0, a = 0, b = 3. Так как числа 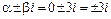 – не корни характеристического уравнения (r = 0), то частное решение имеет вид:
– не корни характеристического уравнения (r = 0), то частное решение имеет вид: 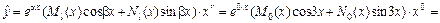
 , где А и В – неопределенные коэффициенты,
, где А и В – неопределенные коэффициенты, 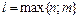 . Найдем
. Найдем  и
и 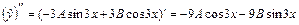 . Подставив
. Подставив  ,
, 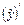 ,
, 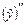 в исходное уравнение, получим
в исходное уравнение, получим 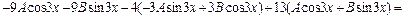
 или
или 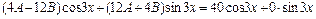 . Приравнивая коэффициенты при синусе и косинусе в обеих частях, получаем систему уравнений
. Приравнивая коэффициенты при синусе и косинусе в обеих частях, получаем систему уравнений 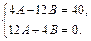 Отсюда A = 1, B = –3. Поэтому частное решение исходного уравнения имеет вид
Отсюда A = 1, B = –3. Поэтому частное решение исходного уравнения имеет вид 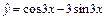 . Следовательно,
. Следовательно, 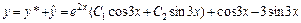 – общее решение исходного уравнения.
– общее решение исходного уравнения.
Для нахождения частного решения исходного уравнения, удовлетворяющего начальным условиям y(0) = 1,  вычислим
вычислим 
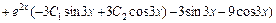 . Подставляя начальные условия в найденное общее решение и его производную, получим систему
. Подставляя начальные условия в найденное общее решение и его производную, получим систему 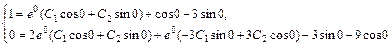 или
или 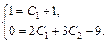 Следовательно, С1 = 0, С2 = 3. Таким образом,
Следовательно, С1 = 0, С2 = 3. Таким образом,  – искомое частное решение.
– искомое частное решение.
3) Найдем общее решение 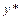 соответствующего однородного уравнения
соответствующего однородного уравнения 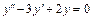 . Характеристическое уравнение
. Характеристическое уравнение 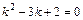 имеет два различных корня
имеет два различных корня 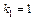 и
и  , значит
, значит 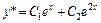 .
.
Найдем частное решение  исходного уравнения. В нем правая часть
исходного уравнения. В нем правая часть  есть формула вида
есть формула вида  , причем n = 0, а a = 1 – корень характеристического уравнения кратности 1 (r = 1). Поэтому частное решение
, причем n = 0, а a = 1 – корень характеристического уравнения кратности 1 (r = 1). Поэтому частное решение 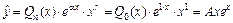 , где А – неопределенный коэффициент. Тогда
, где А – неопределенный коэффициент. Тогда  и
и 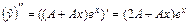 . Подставим
. Подставим  ,
, 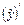 ,
, 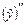 в исходное уравнение и получим
в исходное уравнение и получим  . Сократив оби части равенства на
. Сократив оби части равенства на 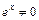 и приведя подобные, получим
и приведя подобные, получим 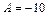 . Поэтому частное решение исходного уравнения имеет вид
. Поэтому частное решение исходного уравнения имеет вид 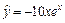 . Следовательно,
. Следовательно, 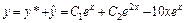 – общее решение исходного уравнения.
– общее решение исходного уравнения.
Для нахождения частного решения исходного уравнения, удовлетворяющего начальным условиям y(0) = 2, 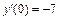 сначала найдем
сначала найдем 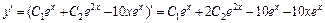 . Подставим начальные условия в найденное общее решение и его производную, получим систему
. Подставим начальные условия в найденное общее решение и его производную, получим систему  или
или 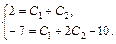 Отсюда С1 = С2 = 1. Итак, частное решение исходного уравнения имеет вид
Отсюда С1 = С2 = 1. Итак, частное решение исходного уравнения имеет вид  .
.
Ответ: 1) 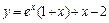 ; 2)
; 2)  ; 3)
; 3) 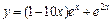 .
.
Задание 3. Написать три первых члена степенного ряда  , найти его область абсолютной сходимости.
, найти его область абсолютной сходимости.
Решение. Запишем три первых члена ряда. При n = 1 получаем первый член ряда: 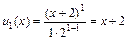 , при n = 2 – второй член:
, при n = 2 – второй член: 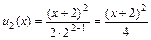 и при n = 3 – третий член ряда:
и при n = 3 – третий член ряда:  .
.
Для данного ряда имеем а = –2,  ,
, 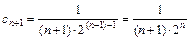 . Найдем радиус сходимости
. Найдем радиус сходимости  . Тогда интервал абсолютной сходимости ряда по формуле (a – R; a + R) есть (–4; 0).
. Тогда интервал абсолютной сходимости ряда по формуле (a – R; a + R) есть (–4; 0).
Теперь выясним поведение ряда на концах интервала сходимости. При x = –4 получаем числовой знакочередующийся ряд 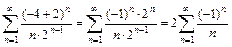 , который сходится согласно признаку Лейбница, т. к. выполняются оба условия признака: 1)
, который сходится согласно признаку Лейбница, т. к. выполняются оба условия признака: 1)  и 2) члены ряда убывают по абсолютной величине
и 2) члены ряда убывают по абсолютной величине  При x = 0 имеем числовой знакоположительный ряд
При x = 0 имеем числовой знакоположительный ряд 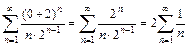 . Это гармонический ряд, который расходится. Таким образом, область абсолютной сходимости исходного ряда имеет вид [–4; 0).
. Это гармонический ряд, который расходится. Таким образом, область абсолютной сходимости исходного ряда имеет вид [–4; 0).
Ответ: 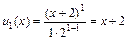 ,
, 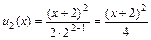 ,
,  ; [–4; 0).
; [–4; 0).
Задание 4. Вычислить определенный интеграл  с точностью до 0,001, разложив подынтегральную функцию в степенной ряд.
с точностью до 0,001, разложив подынтегральную функцию в степенной ряд.
Решение. Для разложения подынтегральной функции в степенной ряд воспользуемся формулой  таблицы основных разложений. Заменив в ней x на x2, получим:
таблицы основных разложений. Заменив в ней x на x2, получим:


для любого  . Так как отрезок интегрирования [0; 0,5] целиком содержится внутри области сходимости ряда, то на основании свойства о почленном интегрировании степенных рядов получим
. Так как отрезок интегрирования [0; 0,5] целиком содержится внутри области сходимости ряда, то на основании свойства о почленном интегрировании степенных рядов получим
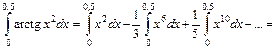

Получили числовой знакочередующийся ряд, удовлетворяющий условиям признака Лейбница: 1) члены знакочередующегося ряда убывают по абсолютной величине: 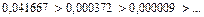 и 2) предел его общего члена при
и 2) предел его общего члена при  равен нулю:
равен нулю:  . Так как |a2| = 0,000372 < 0,001, то приближенное значение суммы S полученного ряда будет равно: S » S1 = a1, так как по следствию из признака Лейбница погрешность вычисления r2 = |S – S1| < |a2| < 0,001.
. Так как |a2| = 0,000372 < 0,001, то приближенное значение суммы S полученного ряда будет равно: S » S1 = a1, так как по следствию из признака Лейбница погрешность вычисления r2 = |S – S1| < |a2| < 0,001.
Таким образом, 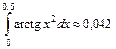 .
.
Ответ: » 0,042.
5.1. Контрольная работа № 5. «Теория вероятностей».
1. Решить задачу.
1. Вероятность изготовления не бракованного пластмассового ведра на станке равна 0,93. Сделано три ведра. Найти вероятность того, что: а) все вёдра не бракованные; б) два ведра не бракованные; в) только одно ведро не бракованное; г) хотя бы одно ведро не бракованное; д) все вёдра бракованные.
2. В начале месяца в аудиторию повесили два новых светильника. Вероятность того, что светильник не выйдет из строя в течение месяца, равна 0,84. Найти вероятность того, что к концу месяца выйдут из строя: а) оба светильника; б) только один светильник; в) хотя бы один светильник; г) ни одного светильника.
3. Вероятность того, что каждый из трёх кассиров занят обслуживанием покупателей, равна 0,7. Найти вероятность того, что в данный момент заняты обслуживанием покупателей: а) все кассиры; б) два кассира; в) только один кассир; г) хотя бы один кассир.
4. Вероятность выпуска стандартной упаковки составляет 0,95. Найти вероятность того, что из трёх сделанных упаковок стандартными окажутся: а) все три; б) только две; в) лишь одна; г) хотя бы одна; д) ни одной упаковки.
5. Прибор состоит из двух узлов, которые во время работы независимо друг от друга могут выходить из строя. Вероятность безотказной работы каждого узла в течение гарантийного срока равна 0,75. Найти вероятность того, что в течение гарантийного срока прибор: а) будет работать исправно; б) выйдет из строя.
6. У фотолюбителя в коробке находится пять одинаковых кассет с фотоплёнками, из которых три плёнки уже отсняты, а две – чистые. Будучи не в состоянии установить, какие из них отсняты, он решает отобрать наугад две плёнки, а остальные проявить. Какова вероятность того, что в отобранных кассетах окажутся чистыми: а) обе плёнки; б) хотя бы одна плёнка?
7. Из автовокзала отправились два автобуса–экспресса. Вероятность своевременного прибытия каждого автобуса в аэропорт равна 0,95. Найти вероятность того, что: а) оба автобуса прибудут вовремя; б) оба автобуса опоздают; в) только один автобус прибудет вовремя; г) хотя бы один автобус прибудет вовремя.
8. Два стрелка произвели по одному выстрелу по мишени. Вероятность поражения мишени каждым из стрелков равна 0,9. Найти вероятность того, что: а) оба стрелка поразят мишень; б) только один стрелок поразит мишень; в) хотя бы один стрелок поразит мишень; г) оба стрелка промахнутся.
9. В офисе работают три вентилятора. Для каждого вентилятора вероятность перегрева к обеденному перерыву составляет 0,8. Найти вероятность того, что к обеденному перерыву перегреются: а) два вентилятора; б) хотя бы один вентилятор.
10. Из трёх орудий произвели залп по цели. Вероятность попадания в цель при одном выстреле равна 0,8. Найти вероятность того, что: а) только один снаряд поразит цель; б) только два снаряда попадут в цель; в) все три снаряда попадут в цель; г) хотя бы один снаряд попадёт в цель.
2. Решить задачу.
1. В магазин поступил одноимённый товар, изготовленный двумя предприятиями. С первого предприятия поступило 150 единиц, из них 30 единиц 1-го сорта, со второго предприятия поступило 200 единиц, из них 50 – 1-го сорта. Из общей массы товара наугад извлекается одна единица. Она оказалась 1-го сорта. Какова вероятность того, что она изготовлена на первом предприятии?
2. Пассажир может приобрести билет в одной из двух касс. Вероятность обращения в первую кассу 0,4, а во вторую – 0,6. Вероятность того, что к моменту прихода пассажира нужные ему билеты будут распроданы, равна 0,35 для первой кассы и 0,7 – для второй. Пассажир посетил одну из касс и приобрёл билет. Какова вероятность того, что он приобрёл билет во второй кассе?
3. В магазин поступила обувь от двух поставщиков. Количество обуви, поступившей от первого поставщика, в два раза больше, чем от второго. Известно, что в среднем 20% обуви от первого поставщика и 35% обуви от второго поставщика имеют различные дефекты отделки верха. Из общей массы наугад отбирают одну упаковку с обувью. Она не имеет дефектов. Какова вероятность того, что её изготовил первый поставщик?
4. В двух одинаковых коробках находится одинаковое количество карандашей «Конструктор». Известно, что 1/3 карандашей в первой коробке и 1/4 карандашей во второй коробке имеют твёрдость ТМ. Наугад выбирается одна коробка и из неё наугад извлекается один карандаш. Он оказался твёрдости ТМ. Какова вероятность того, что он извлечён из первой коробки?
5. Два товароведа производят приёмку партии изделий по качеству. Вероятность того, что очередное изделие попадёт к первому товароведу, равна 0,4, а ко второму – 0,6. Первый товаровед выявляет дефект с вероятностью 0,95, второй – с вероятностью 0,8. Одно из дефектных изделий было признано годным к эксплуатации. Какова вероятность того, что изделие проверял второй товаровед?
6. В магазин от двух поставщиков поступила женская обувь в одинаковых упаковках. От первого поставщика поступило 480 пар, из них 360 пар чёрного цвета. От второго поставщика поступило 320 пар, в том числе 120 пар чёрного цвета. В выбранной наугад упаковке оказалась обувь чёрного цвета. Какова вероятность того, что она поступила от второго поставщика?
7. Два специалиста ОТК завода проверяют качество выпускаемых изделий, причём каждое изделие может с одинаковой вероятностью быть проверено как первым, так и вторым специалистом. Вероятность пропуска дефекта первым специалистом составляет 0,1, а вторым – 0,05. Одно из дефектных изделий было признано качественным. Какова вероятность того, что это изделие проверял первый специалист?
8. В двух больших одинаковых коробках находятся компьютерные дискеты. Известно, что четверть дискет в первой коробке и треть во второй являются чистыми. Студент наугад берёт коробку и вынимает из неё дискету, которая оказалась с записью программ. Какова вероятность того, что он вынул дискету из второй коробки?
9. Покупатель может приобрести нужный ему товар в двух магазинах. Вероятность обращения в эти магазины: 0,3 – в первый и 0,7 – во второй. Вероятность того, что к моменту прихода покупателя товар уже распродан равна 0,2 для 1-го и 0,6 для 2-го магазинов. Покупатель посетил один из магазинов и приобрёл товар. Какова вероятность того, что он купил товар в первом магазине?
10. В торговую фирму поступили телевизоры от трёх поставщиков в отношении 1:4:5. Практика показала, что телевизоры, поступающие от 1-го, 2-го и 3-го поставщиков, не потребуют ремонта в течение гарантийного срока соответственно в 98%, 88% и 92% случаев. Проданный телевизор потребовал ремонта в течение гарантийного срока. Какова вероятность того, что телевизор поступил от третьего поставщика?
3. Дана дискретная случайная величина Х. 1) Составить закон распределения этой случайной величины Х; 2) построить многоугольник распределения вероятностей; 3) найти математическое ожидание, дисперсию и среднее квадратическое отклонение Х.
1. Вероятность, что купленный лотерейный билет окажется выигрышным, равна 0,3. Случайная величина Х – число выигранных билетов из двух купленных.
2. Вероятность попадания при каждом выстреле равна 2/3. Случайная величина Х – число попаданий в мишень при двух выстрелах.
3. Производятся два одиннадцатиметровых удара с вероятностью попадания в ворота при одном ударе 0,7. Случайная величина Х – число попаданий в ворота.
4. Вероятность того, что автомат при опускании одной монеты срабатывает правильно, равна 0,98. Случайная величина Х – число правильных срабатываний автомата, если в наличии всего две монеты.
5. Медсестра закреплена за двумя больными. Вероятность того, что каждый больной потребует внимания медсестры в течение часа, равна 0,4. Случайная величина Х – число вызовов медсестры в течение часа.
6. Устройство состоит из двух независимо работающих элементов. Вероятность отказа каждого элемента равна 0,1. Случайная величина Х – число отказавших элементов.
7. Монета подбрасывается два раза. Случайная величина Х – число выпавших гербов.
8. Вероятность рождаемости мальчика равна 0,51. Случайная величина Х – число мальчиков в семье, имеющей 2 детей.
9. Игральная кость брошена два раза. Случайная величина Х – число появлений шестерки.
10. Появление колонии микроорганизмов данного вида в определенных условиях оценивается вероятностью 0,7. Случайная величина Х – число колоний микроорганизмов в двух наудачу взятых пробах.
4. Непрерывная случайная величина X задана функцией распределения F(x). Найти: 1) плотность распределения f(х); 2) математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины X; 3) построить графики функций F(x) и f(х).
1.  2.
2. 
3.  4.
4. 
5. 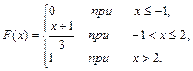 6.
6. 
7. 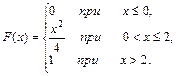 8.
8. 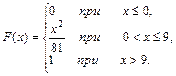
9. 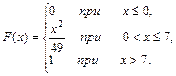 10.
10. 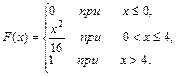
5. Задана плотность распределения непрерывной случайной величины Х. Найти неизвестный параметр С.
1. 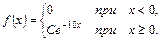 2.
2. 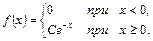
3. 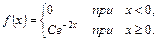 4.
4. 
5.  6.
6. 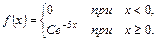
7. 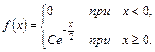 8.
8. 
9.  10.
10. 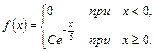
– Конец работы –
Эта тема принадлежит разделу:
Часть 1. ПРОГРАММА КУРСА Элементы векторной алгебры и аналитической геометрии.
Волгоградский государственный архитектурно строительный университет... Волжский институт строительства и технологий...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Образец решения контрольной работы № 4.
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов