рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Образование
- /
- Свойства умножения вектора на число.
Реферат Курсовая Конспект
Свойства умножения вектора на число.
Свойства умножения вектора на число. - раздел Образование, Тема 4. Линейное пространство 1) ...
1)  и
и 

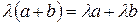 .
.
2)  и
и  вектора
вектора 

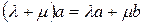 .
.
3)  и
и  вектора
вектора 

 .
.
4)  вектора
вектора 

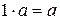 .
.
 Доказательство 1). Пусть для простоты
Доказательство 1). Пусть для простоты  и будем использовать правило параллелограмма для сложения векторов. Если вместо
и будем использовать правило параллелограмма для сложения векторов. Если вместо  и
и 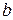 взять
взять 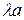 и
и  , то получим подобный параллелограмм и его диагональ соответственно равна
, то получим подобный параллелограмм и его диагональ соответственно равна 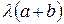 .(см. рис.3)
.(см. рис.3)
Рис.3. Иллюстрация свойства сложения векторов 
Доказательство 2)–4). Очевидно, такое, что получаются коллинеарные вектора.
Теорема 1. Множество векторов пространства образует линейное пространство.
Доказательство. Следует из свойств сложения векторов и умножения на число.∎
Замечание. Можно определить операцию вычитания векторов по формуле  (см.рис.4)
(см.рис.4)
 |
Рис. 4. Вычитание векторов
a) Множество коллинеарных векторов образует линейное пространство
б) Множество компланарных векторов образует линейное пространство.
Далее выясним размерности и базисы перечисленных пространств.
2о. Размерность линейных пространств геометрических векторов.
Теорема 3. Два вектора коллинеарны тогда и только тогда, когда они линейно зависимы.
Доказательство. Если один из векторов нулевой, то очевидно. Поэтому далее предполагаем, что оба вектора ненулевые.
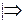 Пусть
Пусть  и
и 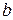 – коллинеарны. Отложим их от одной точки. Пусть
– коллинеарны. Отложим их от одной точки. Пусть 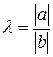 . Тогда если
. Тогда если 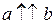 , то
, то 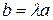 , если
, если 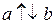 , то
, то  . В обоих случаях
. В обоих случаях  и
и 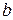 – линейно зависимы.
– линейно зависимы.
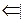 Пусть
Пусть  и
и 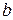 – линейно зависимы, т.е.
– линейно зависимы, т.е. 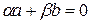 , где
, где  не равно 0. Тогда, если
не равно 0. Тогда, если 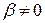 ,
, 
 по определению 10
по определению 10
 и
и 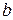 коллинеарны.∎
коллинеарны.∎
Следствие 1. Линейное пространство коллинеарных векторов одномерно и его базисом может служить любой ненулевой вектор.
Следствие 2. Если  и
и 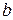 – коллинеарны и
– коллинеарны и 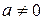 , то
, то 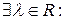
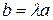 .
.
Доказательство. 
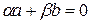 . Если
. Если 



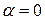 . Т.о.
. Т.о. 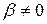

 и
и 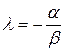 .
.
Теорема 4. Три вектора компланарны тогда и только тогда, когда они линейно зависимы.
Доказательство. Будем предполагать, что никакие два вектора из трех не коллинеарны, т.к. иначе утверждение очевидно в силу §11 (свойство линейно зависимых векторов).
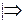 Пусть вектора
Пусть вектора  компланарны. Перенесем их в точку O, проведем через конец вектора c прямые, параллельные векторам
компланарны. Перенесем их в точку O, проведем через конец вектора c прямые, параллельные векторам  и
и 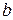 и рассмотрим параллелограмм
и рассмотрим параллелограмм 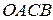 .(см. рис. 5) Векторы
.(см. рис. 5) Векторы  и
и  ,
, 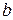 и
и  – коллинеарны
– коллинеарны 

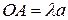 ,
,  . Но
. Но 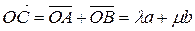

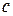 ,
,  ,
, 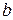 – линейно зависимы.
– линейно зависимы.

Рис.5. Иллюстрация доказательства теоремы 4.
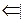 Пусть
Пусть  ,
, 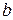 ,
, 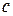 – линейно зависимы. Тогда
– линейно зависимы. Тогда  , одновременно не равные нулю:
, одновременно не равные нулю: 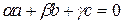 . Если, например,
. Если, например, 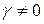 , то
, то 

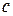 – диагональ параллелограмма со сторонами, параллельными
– диагональ параллелограмма со сторонами, параллельными  и
и 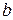

 ,
, 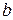 ,
, 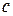 лежат в одной плоскости, т.е они компланарны.∎
лежат в одной плоскости, т.е они компланарны.∎
Следствие. Линейное пространство компланарных векторов двумерно и его базисом может служить любая пара неколлинеарных векторов.
Теорема 5. Любые четыре вектора линейно зависимы.
Доказательство. Предположим, что никакие три из векторов  не компланарны (иначе они линейно зависимы) очевидно. Остальное следует из (рис.6) по аналогии с доказательством теоремы 4. Через точку D проведем три плоскости, параллельные парам векторов {
не компланарны (иначе они линейно зависимы) очевидно. Остальное следует из (рис.6) по аналогии с доказательством теоремы 4. Через точку D проведем три плоскости, параллельные парам векторов { ,
, 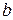 }; {
}; { ,
, 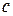 };{
};{ 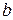 ,
, 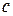 }.
}.
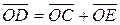 ,
, 

 .
. 
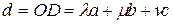

 ,
, 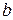 ,
, 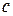 ,
,  – линейно зависимы.∎
– линейно зависимы.∎
 | |||
| |||
B


|
 b
b
 | |||
| |||
Рис.6. Иллюстрация доказательства 5.
Следствие. Линейное пространство всех геометрических векторов трехмерное. Его базисом могут служить любые три некомпланарных вектора.
3о. Проекции вектора на ось
Пусть в пространстве задана некоторая прямая 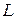 и единичный вектор
и единичный вектор  .
.
Определение 11.Осью 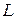 будем называть прямую, по которой задано направление. Направление оси задается вектором
будем называть прямую, по которой задано направление. Направление оси задается вектором 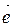 (направляющий вектор оси).
(направляющий вектор оси).

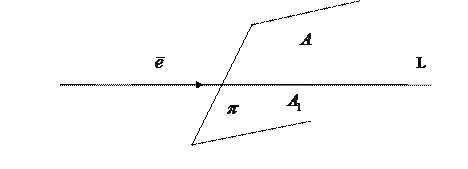
Рис.7. Проекция точки А на ось L.
Пусть 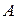 – точка непринадлежащая
– точка непринадлежащая 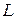 . Проведем через точку
. Проведем через точку 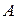 плоскость
плоскость 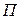 ^
^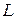 . Получим точку
. Получим точку  , которая называется проекцией (ортогональной проекцией) точки
, которая называется проекцией (ортогональной проекцией) точки 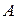 на ось
на ось 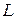 . Обозначение:
. Обозначение:  (см. рис.7).
(см. рис.7).
Если наряду с точкой 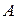 взять точку
взять точку  , то можно построить
, то можно построить  .
.
Определение 2.Так построенный вектор  называется векторной проекцией вектора
называется векторной проекцией вектора  на ось
на ось 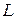 . Обозначают:
. Обозначают: 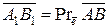 .
.
Иногда говорят, что  есть компонента вектора
есть компонента вектора  на оси
на оси 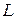 .
.
Вектора  и
и 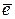 – коллинеарны Þ
– коллинеарны Þ 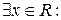
 .
.
Определение 13.Такое число 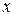 называется скалярной проекцией (проекцией) вектора
называется скалярной проекцией (проекцией) вектора  на ось
на ось 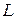 . Пишут:
. Пишут:  .
.
Таким образом 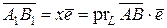 .
.
Легко видеть, что  Û
Û  ^
^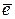 .
.
– Конец работы –
Эта тема принадлежит разделу:
Тема 4. Линейное пространство
о Определение и простейшие свойства... Пусть даны поле с элементами называемыми скалярами и обозначаемыми малыми... Определение Множество вместе с заданными на нем операциями сложения векторов и умножения вектора на скаляр...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Свойства умножения вектора на число.
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов