рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Образование
- /
- Непрерывные случайные величины
Реферат Курсовая Конспект
Непрерывные случайные величины
Непрерывные случайные величины - раздел Образование, Функции распределения, плотность распределения Рассмотрим Случай, Когда Множество Возможных Значений Случайной Величины Несч...
Рассмотрим случай, когда множество возможных значений случайной величины несчетно.
Определение. Случайная величина X с непрерывной функцией распределения  называется непрерывной случайной величиной.
называется непрерывной случайной величиной.
Определение. Плотностью распределения (плотностью вероятности) случайной величины X называется неотрицательная кусочно-непрерывная функция 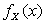 , для которой при любом
, для которой при любом  выполняется соотношение
выполняется соотношение
 .
.
Определение. Случайная величина, у которой существует плотность вероятности, называется абсолютно непрерывной, или случайной величиной непрерывного типа (сокращенно СВНТ).
Замечание. Кроме абсолютно непрерывных случайных величин существуют непрерывные случайные величины, называемые сингулярными, которые не имеют плотности вероятности. В дальнейшем такие случайные величины не рассматриваются.
Покажем, что для СВНТ X  для произвольного фиксированного
для произвольного фиксированного  . Действительно, из равенства
. Действительно, из равенства
 ,
,
равносильного
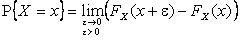 ,
,
следует, что вероятность «попасть в точку» для СВНТ X равна нулю.
Из определения следуют свойства плотности распределения 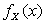 :
:
1. 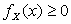 для всех
для всех  (условие неотрицательности плотности).
(условие неотрицательности плотности).
2.  (условие нормировки плотности).
(условие нормировки плотности).
3. 
 .
.
Замечание. Таким образом, через плотность вероятности 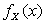 можно вычислить вероятность
можно вычислить вероятность  для любого
для любого 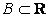 .
.
4.  в точках непрерывности плотности
в точках непрерывности плотности 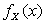 .
.
Пример 2.1.10. Даны функции:
 ,
, 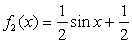 ,
, 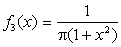 .
.
Являются ли эти функции плотностями вероятности?
Решение. Для функции  не выполнено условие неотрицательности, т.к.
не выполнено условие неотрицательности, т.к.  для всех
для всех  . Для функции
. Для функции 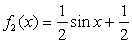 не выполнено условие нормировки, т.к. интеграл
не выполнено условие нормировки, т.к. интеграл 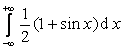 расходится. Наконец, для функции
расходится. Наконец, для функции 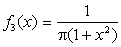 выполнены условия неотрицательности и нормировки, поскольку, очевидно,
выполнены условия неотрицательности и нормировки, поскольку, очевидно,  для всех действительных x и
для всех действительных x и
 .
.
Ответ: плотностью распределения является только  .
.
Пример 2.1.11. СВНТ X задана функцией распределения
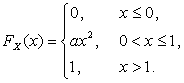
Найти: 1) коэффициент a; 2) 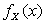 и построить ее график; 3)
и построить ее график; 3) 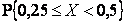 .
.
Решение. 1) Так как  непрерывна, то
непрерывна, то 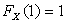 , т.е.
, т.е.  . Отсюда
. Отсюда 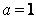 .
.
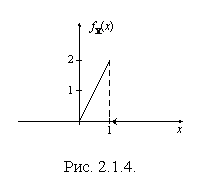 2) Плотность распределения
2) Плотность распределения  . Поэтому функция плотности
. Поэтому функция плотности 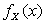 :
:

График плотности 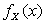 приведен на рис. 2.1.4.
приведен на рис. 2.1.4.
3)  .
.
Ответ: 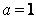 ,
,  ,
,  .
.
Пример 2.1.12. СВНТ X задана функцией плотности

Найти: 1) коэффициент a; 2)  и построить ее график; 3)
и построить ее график; 3)  .
.
Решение. 1)  . Отсюда
. Отсюда  .
.
2) По определению  .
.
Пусть  , тогда
, тогда 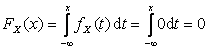 .
.
Пусть  , тогда
, тогда
 .
.
Пусть  , тогда
, тогда  .
.
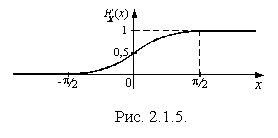 Таким образом, функция распределения
Таким образом, функция распределения  :
:
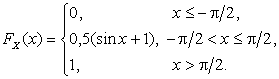
График функции распределения  приведен на рис. 2.1.5.
приведен на рис. 2.1.5.
3)  .
.
Ответ:  .
.
– Конец работы –
Эта тема принадлежит разделу:
Функции распределения, плотность распределения
функции распределения плотность распределения... Мат ожидание дисперсия... Практика...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Непрерывные случайные величины
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов