рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Образование
- /
- Механическая интерпретация математического ожидания и дисперсии
Реферат Курсовая Конспект
Механическая интерпретация математического ожидания и дисперсии
Механическая интерпретация математического ожидания и дисперсии - раздел Образование, Функции распределения, плотность распределения Пусть На Прямой В Точках ...
Пусть на прямой в точках  расположены точечные массы
расположены точечные массы  ,
,  . В этом случае
. В этом случае  – центр тяжести,
– центр тяжести, 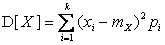 – момент инерции масс
– момент инерции масс 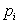 относительно центра тяжести. Таким образом, математическое ожидание характеризует место, вокруг которого группируются массы
относительно центра тяжести. Таким образом, математическое ожидание характеризует место, вокруг которого группируются массы 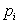 , а дисперсия – степень разбросанности этих масс около математического ожидания.
, а дисперсия – степень разбросанности этих масс около математического ожидания.
В заключение этого пункта вычислим математическое ожидание, дисперсию и среднее квадратическое отклонение  (здесь
(здесь  ):
):

| ||
| P | q | p |
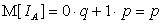 ,
,
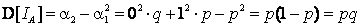 ,
,  .
.
Пример 2.1.17. Закон распределения случайной величины X имеет вид:
| X | |||
| P | 0,1 | 0,2 | x |
Найти x. Составить функцию распределения. Вычислить:  ,
, 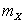 ,
,  и
и  .
.
Решение. Согласно условию нормировки имеем уравнение:  . Отсюда
. Отсюда  . Далее, воспользовавшись рядом распределения, найдем:
. Далее, воспользовавшись рядом распределения, найдем:
 ,
,
 ,
,
 ,
,
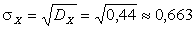 .
.
Ответ:  ,
, 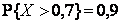 ,
, 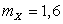 ,
, 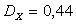 ,
,  .
.
Пример 2.1.18. Известно, что случайная величина X, принимающая два значения  и
и  , имеет математическое ожидание, равное 2,2. Построить ряд распределения случайной величины X, найти дисперсию, среднее квадратическое отклонение и составить функцию распределения.
, имеет математическое ожидание, равное 2,2. Построить ряд распределения случайной величины X, найти дисперсию, среднее квадратическое отклонение и составить функцию распределения.
Решение. Пусть  . Тогда, согласно условию нормировки,
. Тогда, согласно условию нормировки,  . Используя определение математического ожидания, получим
. Используя определение математического ожидания, получим  . Имеем уравнение
. Имеем уравнение  , откуда находим
, откуда находим  . Ряд распределения имеет вид:
. Ряд распределения имеет вид:
| X | ||
| P | 0,8 | 0,2 |
Теперь вычислим дисперсию и среднее квадратическое отклонение:
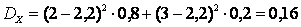 ;
;  .
.
Согласно определению функция распределения имеет вид

Ответ:  ,
,  ,
, 
Пример 2.1.19. Возможные значения случайной величины X таковы:  ,
,  ,
,  . Известно, что
. Известно, что  ,
,  . Найти вероятности, соответствующие возможным значениям X, и записать ряд распределения.
. Найти вероятности, соответствующие возможным значениям X, и записать ряд распределения.
Решение. Ряд распределения, с учетом возможных значений случайной величины X, будет выглядеть следующим образом:
| X | |||
| P | 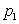
| 
| 
|
Найдем вероятности 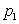 ,
,  и
и  , соответствующие возможным значениям X.
, соответствующие возможным значениям X.
По условию  , поэтому имеем первое уравнение, связывающее
, поэтому имеем первое уравнение, связывающее 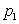 ,
,  и
и  :
:  . Аналогично из условия
. Аналогично из условия  получим второе уравнение:
получим второе уравнение:  . Третье уравнение возникает из условия нормировки:
. Третье уравнение возникает из условия нормировки: 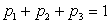 . Итак, имеем систему:
. Итак, имеем систему:

Решением системы, опуская промежуточные выкладки, являются следующие числа:  ,
,  ,
,  .
.
Ответ: ряд распределения имеет вид
| X | |||
| P | 0,2 | 0,3 | 0,5 |
Пример 2.1.20. Плотность 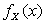 случайной величины X представлена на графике (рис. 2.1.7). Найти константу h. Составить функцию распределения
случайной величины X представлена на графике (рис. 2.1.7). Найти константу h. Составить функцию распределения  и построить ее график. Найти
и построить ее график. Найти 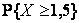 , математическое ожидание и дисперсию случайной величины Х.
, математическое ожидание и дисперсию случайной величины Х.
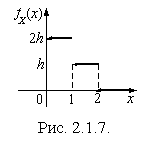 Решение. 1) Найдем константу h из условия нормировки. Имеем уравнение
Решение. 1) Найдем константу h из условия нормировки. Имеем уравнение  , или, исходя из геометрического смысла интеграла,
, или, исходя из геометрического смысла интеграла,  . Отсюда
. Отсюда  . Таким образом, функция плотности
. Таким образом, функция плотности 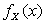 имеет вид:
имеет вид:

2) По определению  .
.
Пусть  , тогда
, тогда 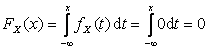 .
.
Пусть  , тогда
, тогда  .
.
Пусть  , тогда
, тогда
 .
.
Пусть 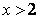 , тогда
, тогда  .
.
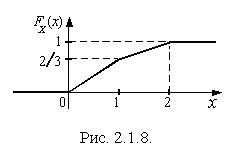 Таким образом, функция распределения
Таким образом, функция распределения  :
:
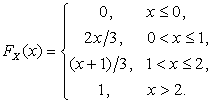
График функции распределения  приведен на рис. 2.1.8.
приведен на рис. 2.1.8.
3)  .
.
4) По определению математического ожидания  , поэтому:
, поэтому:
 .
.
По определению дисперсии 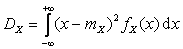 , поэтому:
, поэтому:
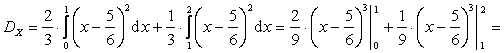
 .
.
Ответ: 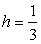 ,
, 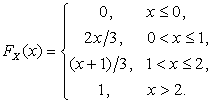 ,
,  ,
, 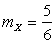 ,
, 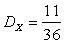 .
.
– Конец работы –
Эта тема принадлежит разделу:
Функции распределения, плотность распределения
функции распределения плотность распределения... Мат ожидание дисперсия... Практика...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Механическая интерпретация математического ожидания и дисперсии
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов