рефераты конспекты курсовые дипломные лекции шпоры

Раздел Образование
/
Моменты распределения случайной величины

Реферат Курсовая Конспект

Выберите учебное заведение

Моменты распределения случайной величины

Моменты распределения случайной величины - раздел Образование, Функции распределения, плотность распределения Среди Числовых Характеристик Особое Значение Имеют Моменты – Начальные И Цент...

Среди числовых характеристик особое значение имеют моменты – начальные и центральные.

Определение. Начальным моментом s-го порядка случайной величины Х называется действительное число 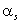, определяемое по формуле:

, если X – СВДТ;

, если X – СВНТ.

Замечание. Начальный момент 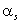существует, если ряд (соответственно интеграл) в правой части каждой из этих формул сходится абсолютно.

Замечание. Иногда используются абсолютные начальные моменты s-го порядка случайной величины X:

, если X – СВДТ;

, если X – СВНТ;

Определение. Начальный момент первого порядка называется математическим ожиданием (средним значением по распределению) случайной величины Х.

Математическое ожидание случайной величины X обозначается 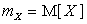и выражается через ее закон распределения с помощью формулы:

, если X – СВДТ;

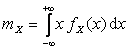, если X – СВНТ.

Математическое ожидание в теории вероятностей относится к типу характеристик положения (см. далее мода, медиана).

Определение. Случайная величина называется центрированной, если ее математическое ожидание равно нулю.

Общепринятым для центрированной случайной величины является обозначение 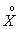. По определению .

Пример 2.1.13. Закон распределения случайной величины X имеет вид:

X	–1
P	0,1	0,2	0,3	0,4

Вычислить 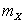и .

Решение. По определению 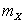и :

;

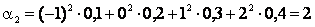Ответ: , .

Пример 2.1.14. Дана функция плотности случайной величины Х:

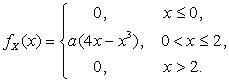
Определить а, затем найти 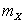и случайной величины Х.

Решение. Константа a ищется из условия нормировки . Имеем уравнение:

, или .

Отсюда , и функция плотности примет вид:

По определению математического ожидания СВНТ X:

Найдем теперь начальный момент третьего порядка :

Ответ: , , .

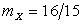Пример 2.1.15. Плотность 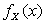случайной величины X представлена на графике (рис. 2.1.6). Найти константу h и математическое ожидание случайной величины Х.

Решение. Найдем константу h из условия нормировки. Имеем уравнение , или, исходя из геометрического смысла интеграла, 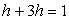. Отсюда .

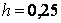По определению математического ожидания:

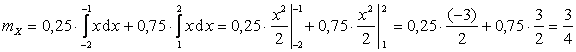Ответ: , .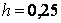

Развернуть

Открыть в широком формате

– Конец работы –

Эта тема принадлежит разделу:

Функции распределения, плотность распределения

функции распределения плотность распределения... Мат ожидание дисперсия... Практика...

Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Моменты распределения случайной величины

Что будем делать с полученным материалом:

Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:

Все темы данного раздела:

Случайной величины
Пусть (, F, P) – произвольное вероятностное пространство. Определение

Дискретные случайные величины
Определение. Случайная величина называется дискретной, или дискретного типа (сокращенно СВДТ), если множество ее возможных значений конечно или счетно. Прост

Непрерывные случайные величины
Рассмотрим случай, когда множество возможных значений случайной величины несчетно. Определение. Случайная величина X с непрерывной функцией распределения

Числовые характеристики случайных величин
В предыдущих пунктах была описана исчерпывающая характеристика любой случайной величины – ее закон распределения. Универсальным видом закона распределения случайной величины является функ

Статистическое истолкование математического ожидания
Пусть в некоторой лотерее имеется один выигрыш, размер которого случаен и равен или , или

Механическая интерпретация математического ожидания и дисперсии
Пусть на прямой в точках расположены точечные массы

Мода, медиана и квантили
Математическое ожидание не единственная характеристика положения, применяемая в теории вероятностей. Часто применяются и другие, например, мода и медиана. Определение.

Упражнения
2.1.1. Функция распределения случайной величины X непрерывна. Может ли случайная величина X быть СВДТ? 2.1.2. Случайная величина X пр

Биномиальное распределение
Определение. СВДТ Х имеет биномиальное распределение, если ее возможные значения (реализации)

Распределение Пуассона
Определение. СВДТ Х имеет распределение Пуассона с параметром , ес

Простейший пуассоновский поток
На практике часто встречаются ситуации, где имеет место распределение Пуассона. Рассмотрим следующую задачу. Пусть на оси времени 0t случайным образом возникают точки – моменты появ

Геометрическое распределение
Определение. СВДТ Х имеет геометрическое распределение, если ее возможные значения (реализации)

Упражнения
Биномиальное распределение 2.1.16.Вероятность брака при производстве приборов составляет 10%. С какой вероятностью среди 6 приборов, взятых для контроля, окажется р

Равномерное распределение
Определение. СВНТ Х распределена равномерно на отрезке , если плот

Показательное (экспоненциальное) распределение
Определение. СВНТ Х имеет показательное (экспоненциальное) распределение с параметром

Нормальное распределение
Определение. СВНТ Х имеет нормальное (гауссовское) распределение с параметрами

Асимметрия и эксцесс
Нормальное распределение имеет широкое распространение в прикладных задачах. Поэтому при изучении распределений, отличных от нормального, возникает необходимость количественно оценить это различие.

Упражнения
Равномерное распределение 2.1.36.Случайная величина X имеет равномерное распределение на отрезке