Ответы, указания, решения

2. Указание. Утверждение непосредственно проверяется по определению.

3. Доказательство. Докажем индукцией относительно числа векторов в системе. Для одного вектора утверждение следует из задачи 8 п.1.3. Предположим, что утверждение верно для систем с 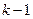векторами. Пусть 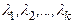- попарно различные собственные значения матрицы А, - собственные векторы, им соответствующие. Если система векторов - линейно зависима, то нулевой вектор представим в виде ненулевой комбинации этих векторов: 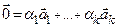- Умножим обе части этого равенства слева на матрицу :

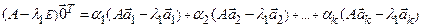
или

.

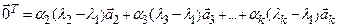Так как по индуктивному предположению система векторов 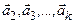линейно независима, то из последнего равенства следует, что все коэффициенты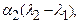 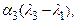… , 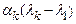равны нулю. Но тогда 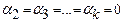, ибо все числа 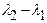, ,…, 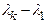отличны от нуля. Следовательно, 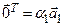, т.е. . Получено противоречие, поскольку рассмотренная комбинация векторов ненулевая.

4. Доказательство.Поскольку предполагается, что обратная матрица существует, то матрица А не имеет нулевого собственного значения(см. задачу5 и следствие2.2).Предположим, что- собственное значение матрицы А. Это равносильно равенству (теорема 4.1). Разделив каждую строку матрицы 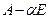на 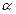, получим равенство 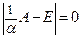. Теперь умножим обе части этого равенства на :

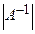И, опять таки, по теореме 4.1 последнее равенство равносильно тому, что - собственное значение матрицы . Утверждение доказано.

5. Указание:воспользоваться следствием 1.3.

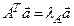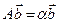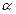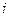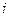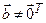6. Доказательство.Согласно теореме 4.2 и следствию 4.1, существует положительный вектор , такой, что . Пусть теперь - произвольный неотрицательный собственный вектор матрицы А, т.е. для некоторого собственного значения . Если -я координата в равна нулю, то произведение -й строки матрицы А на было бы равно нулю, что невозможно ввиду , и . Поэтому - положительный собственный вектор. Применяя теоремы 1.1 и 1.14, с одной стороны, имеем:

С другой стороны,

Откуда

.

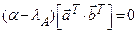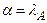Но ввиду того, что . Поэтому , что и требовалось доказать.

?. Доказательство.Векторы и соответствуют максимальному собственному значению матрицы А (см. задачу 6), т.е. 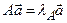, 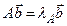. Обозначим через 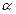положительное число, равное наименьшему из чисел 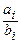, где , - -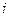е координаты векторов и соответственно. Тогда , причем хотя бы одна координата вектора равна нулю (согласно выбору 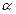). Но

что означает, что - собственный, не являющийся положительным, неотрицательный вектор матрицы А, что будет противоречить утверждению задачи 6, если только - ненулевой. Поэтому , что и требовалось доказать.

8. Решение.Для определения собственных значений матрицы А составим характеристическое уравнение :

.

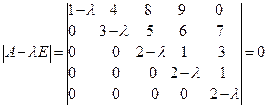Так как определитель треугольной матрицы равен произведению элементов на главной диагонали, то данное уравнение равносильно уравнению , откуда получаем три собственных значения , . Для определения собственных векторов, им соответствующих, необходимо решить три однородные системы линейных уравнений 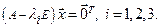Применим алгоритм метода Гаусса для решения первой из них:

.

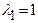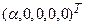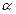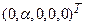Итак, все собственные векторы, соответствующие имеют вид , где - любое число. Аналогично устанавливается, что все собственные векторы, соответствующие , имеют вид , где 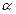- любое число. Решим последнюю систему:

Итак, 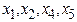- базисные переменные, - свободная переменная:

.

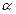Поэтому собственные векторы, соответствующие , имеют следующий вид: , - любое число.