РАЗДЕЛ 1. Дифференциальное исчисление
РАЗДЕЛ 1. Дифференциальное исчисление
Лекции 2 и 3. Предел функции
Понятие предела функции
Пусть функция f(x) определена в некоторой окрестности X точки a, кроме, быть может, самой точки a. Определение 1(определение по Коши): Число b называется пределом функции f(x)… Точка а – точка прикосновения множества D (допустимых значений x), т.е. точка, в любой окрестности которой находятся…Предел функции в бесконечности
Определение.Число b называется пределом функции у=f(x) при х, стремящемся к бесконечности (x→∞), если для любого сколь угодно малого… Данное определение при x→∞ предполагает неограниченное возрастание… Неравенство х > S определяет интервал (S; +∞), который называется окрестностью в точке а = +∞ при…Бесконечно малые величины
Определение. Функция называется a(х) называется бесконечно малой величиной в какой-то точке a, если она имеет нулевой предел в этой точке: . Пример 1. α(x) = 4x – 20 – бесконечно малая величина в точке х = 5, так… Пример 2. β(x) = ln(3x – 8) – бесконечно малая величина в точке х = 3, так как при х®3 будет .Свойства бесконечно малых величин
Пример 3. α(x) = 4x – 20 и β(x) = ln(3x – 14) – бесконечно малые величины в точке х=5. Тогда при х®5 будет . 2. Произведение бесконечно малой величины на ограниченную функцию (в том числе на постоянную или на другую бесконечно…Бесконечно большие величины
Определение. Функция f(x) называется бесконечно большой величиной в какой-то точке a прикосновения множества допустимых значений х, если для любого… Иногда говорят, что бесконечно большой величиной называется переменная… Предел бесконечно большой величины равен бесконечности: .Свойства бесконечно больших величин
1. Произведение бесконечно большой величины на функцию, имеющую ненулевой предел, - бесконечно большая величина.
2. Сумма бесконечно большой величины и ограниченной функции - бесконечно большая.
3. Частное от деления бесконечно большой величины на функцию, имеющую ненулевой предел, - бесконечно большая величина.
Связь между бесконечно большой и бесконечно малой функциями
и . Данную связь символически запишем как и . Пример 1. => – есть бесконечно малая при х®∞, так как по мере неограниченного возрастания х абсолютное…Основные свойства пределов (теоремы о пределах)
Докажем это свойство. Предположим противное, т.е. что функция f(x) имеет два разных предела b и с: , , b ≠ c. Поскольку утверждения «число b есть предел величины у» и «разность у – b есть бесконечно малая величина» равнозначны,…Виды неопределенностей
Соотношения вида являются примерами определенностей, так как . Для раскрытия неопределенностей существуют различные методы. Некоторые из них сводятся к определенным преобразованиям,…Первый и второй замечательные пределы
1-й замечательный предел: . Означает, что sinх ~ х (эквивалентные бесконечно малые) при достаточно малых… Используется при вычислении пределов выражений, содержащих тригонометрические функции.Сравнение бесконечно малых
Пример 1. α(х)=6х; β(х)=2х – бесконечно малые при х®0. При х®0 , т.е. функция при х®0 не бесконечно малая. Более того, предел… В зависимости от вида бесконечно малых функций символ может быть равен произвольному числу или символу ∞.Пример 2.
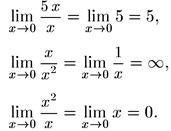
Поэтому частное бесконечно малых называют неопределенностью вида 
, а нахождение предела этой дроби называют раскрытием неопределенности.
Определение 1. Если отношение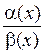 
стремится к конечному пределу, не равному нулю, то α(х) и β(х) называются бесконечно малыми одного порядка малости.
Определение 2.Если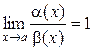 
, то α(х) и β(х) называются эквивалентными бесконечно малыми, ведут себя «одинаково» и обозначаются α(х) ~ β(х).
Например, функции ln(1 + x) их – эквивалентные (ln(1 + x) ~х) при х®0, так как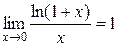 
(см. пример 3 из п.8).
Таблица эквивалентных бесконечно малых функций
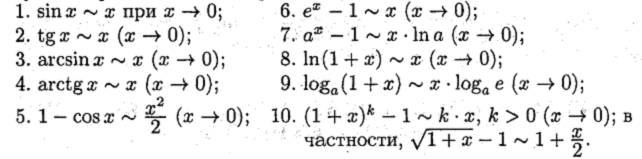
Если α(х) – бесконечно малая при х®а, тогда
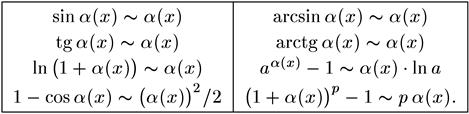
Пример 3.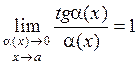
.
Пример 4.Покажем, что ex – 1 ~ x, при х®0, т.е.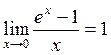 
.
Решение. Положим ex – 1 = y или ex = y + 1. Отсюда x = ln(y +1). Видно, что y®0 при х®0.
Следовательно,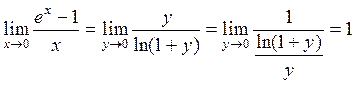 
.
Поэтому ex – 1 ~ x.