Теоретический материал иллюстрируется большим количеством примеров и задач различной трудности
Введение
Данное пособие является составной частью учебного комплекса по курсу высшей математики, которое может быть полезно для организации учебного процесса на факультете дистанционного обучения при самостоятельной подготовке студентов к экзаменам. Оно поможет без помощи преподавателя организовать планомерное изучение материала не только основных понятий и положений теории, но и основных приемов и методов решения задач.
В учебном пособии рассматриваются следующие темы: введение в математический анализ, дифференциальное исчисление функций одной переменной, на которых базируется вся математика. Учебное пособие создано на основе опыта преподавания высшей математики в Комсомольском-на-Амуре государственном техническом университете на технических и гуманитарных факультетах.
Теоретический материал иллюстрируется большим количеством примеров и задач различной трудности.
После каждого раздела приводятся экзаменационные вопросы. Более подробное изложение данного материала можно найти в книгах, учебных пособиях и монографиях, указанных в списке литературы.
Специфика работы с пособием состоит в том, что сначала необходимо ознакомиться с базовыми понятиями и методами математического анализа, изложенными в соответствующих разделах, затем изучить практическую часть (главу 3), а затем перейти к выполнению контрольной работы, предусмотренной программой. Выполненную контрольную работу следует направить на рецензирование. В случае если рецензент обнаружит ошибки в контрольной работе, рекомендуется проработать материал до полного усвоения неясностей, сделать работу над ошибками в той же тетради, в которой была выполнена контрольная работа, и вернуть ее на повторное рецензирование.
Последним этапом работы с данным пособием является экзамен (зачет), вопросы к которому также приведены в заключительной части данного пособия.
ГЛАВА 1. ВВЕДЕНИЕ В МАТЕМАТИЧЕСКИЙ АНАЛИЗ
Логическая и математическая символика
Математические символы: Например, применяя символ «>» к числам a, b, получим запись «a > b»,… Наряду с математической символикой в математике широко используется логическая символика, применяемая к высказываниями…Множества
В математическом анализе чаще всего рассматриваются числовые множества, за некоторыми из них закреплены специальные обозначения. Так, множество всех… Рациональным называется число, которое можно представить в виде отношения двух… Известно, что любое рациональное число можно представить десятичной дробью, конечной и бесконечной периодической.…Функции
Пример 1. Для функции y = область определения A= (–¥, –1]È[1, +¥), множество значений B= [0, +¥). Пример 2. y = , A= R, B= (–¥, +1]. Замечание. Иногда рассматривают многозначные функции, допуская, что каждому значению xÎA, соответствует одно или…Способы задания функции
Аналитический способ: связь между аргументом x и функцией y задается формулой, при этом на разных участках области определения она может задаваться различными формулами (см. пример 2) . В примерах 1, 2 функции заданы аналитически.
Табличный способ: функция задается таблицей отдельных значений аргумента и соответствующих значений функции. Такими являются таблицы тригонометрических функций, таблицы логарифмов и т.д.
Графический способ: в этом случае соответствие между значениями x и y задается с помощью графика.
Среди числовых функций особое место занимают функции с областью определения A = N. Пусть аргумент функции f(x) принимает только значения 1, 2, 3,....n,...
Обозначим f(1) = a1, f(2) = a2, ..., f(n) = an, ... Такую функцию называют последовательностью, a1 – первый член, ..., an – n-й член этой последовательности.
Рассмотрим свойства, которыми могут обладать (или не обладать) некоторые функции.
Функция f(x) называется возрастающей на множестве M (строго), если большему значению аргумента соответствует большее значение функции.
Символически это может быть записано так: "x1, x2ÎM(x1 < x2 ® f(x1) < f(x2)).
Функция f(x) называется убывающей (строго) на множестве M, если большему значению аргумента соответствует меньшее значение функции. Символически:
"x1, x2ÎM(x1< x2 ® f(x1) > f(x2)).
Функция, убывающая или возрастающая на множестве M, называется монотонной на множестве M.
В качестве примера рассмотрим функцию y = x2. На интервале (–¥, 0) это убывающая функция, а на интервале (0, + ¥ ) – возрастающая.
Функция f(x) называется ограниченной сверху на множестве M, если существует такое число k, что для любого значения xÎMf(x) < k.
Символически это может быть записано так: $k "xÎM (f(x) < k).
Аналогично дается определение функции, ограниченной снизу.
Если функция ограничена и сверху, и снизу, то она называется ограниченной. Так, функция y = 
ограничена снизу на множестве A (пример 1), а функция из примера 2 ограничена сверху на множестве R.
Функция f(x) называется четной, если "xÎA (f(–x) = f(x)), и называется нечетной, если "xÎA (f(–x) = –f(x)).
Например, функция y = x2 является четной, а y = sinx – нечетной.
Функция f(x) называется периодической с периодом T (T ¹ 0 ), если
"xÎA(f(x + T) = f(x)).
Известно, что все тригонометрические функции являются периодическими.
Введем важные понятия сложной и обратной функции.
Если переменная y является функцией от x, y = f(x); а x – функция от переменной t: x = j(t), то y = f(j(t)) является функцией от t и называется сложной функцией или функцией от функции.
Например, пусть y = x2, x = sint, тогда функция y = (sint)2 является сложной.
Пусть y = f(x) с областью определения A и множеством значений B такова, что для любого значения yÎB существует единственное значение xÎB, такое, что f(x) = y, тогда переменная x является функцией от y, обозначим x = j(y). Эту функцию называют обратной для y = f(x). Для обратной функции x = j(y) область определения B, а множество значений A. Иногда функцию, обратную к функции y = f(x), обозначают: 
.
Например, для функции y = x2 с областью определения [0, +¥) и таким же множеством значений обратной является функция: x =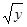
.
В дальнейшем часто будет использоваться понятие абсолютной величины числа, а также понятие e – окрестности точки.
Абсолютной величиной числа a называется неотрицательное число, обозначаемое |a|, такое, что
|a| = 
.
Неравенство |x| < m ( m > 0 ) равносильно двойному неравенству –m < x < m, неравенство |x – x0| < e (e > 0) равносильно x0 – e < x< x0 + e. Множество точек с таким свойством (рис. 1.1) является интервалом (x0 – e, x0 + e) и называется e – окрестностью точки x0 (рис. 1.1).
Пределы функции на бесконечности
Предел функции при x ® +¥ Пусть функция y = f(x) определена на множестве всех действительных чисел R или… Число b называют пределом функцииf(x) при стремлении x к +¥ (x® +¥), если значения f(x) приближаются к числу b…Предел последовательности
Число b называется пределом последовательности {an}, если для любого e > 0 существует такое натуральное число n0, что для всех натуральных n,… Доказать самостоятельно, что = 0. Предел функции при x® -¥Предел функции в точке
Дадим сначала описательное определение предела функции в точке и приведем пример. Число b называется пределом функции f(x) в точкеx0 (x ® x0), если значения… Пример 1. Функция y = определена во всех точках числовой оси, за исключением x0 = 2. Найдем f(x), для этого вычислим…Левосторонний и правосторонний пределы функции в точке
Пусть d > 0. Интервал (a, x0) называется левой полуокрестностью точки x0, интервал (x0 – d, x0) – левой d-полуокрестностью точки x0. Интервалы… Пусть f(x0) определена в левой полуокрестности… Число b называется левосторонним пределом функции f(x) в точке x0 (обозначение: f(x) = b), если для любого e > 0…Бесконечно-малые функции и их свойства
Используя определение предела фикции при х ® +¥, можно перефразировать этог определение: функция a(х) называетсябесконечно малой при х ® +¥,… Символически это выглядит так: ε > 0x0(|(х)|<ε). Аналогично формулируются определения б.м. при x ® +¥, х ® x0, и т.д.Основные теоремы о пределах
Доказательство.Пусть f (x) = b. Рассмотрим функцию a(x) = f(x) – b и покажем, что a(x) – б.м. при x ® +¥ . Из определения f (x) = b имеем, что "e > 0 $x0 "x > x0 |f (x)… Итак, из равенства a(x) = f(x) – b имеем f(x) = b + a(x), где a(x) – б.м. при x ® +¥.Первый замечательный предел
Рассмотрим функцию y = 
, аргумент x (как всегда в математическом анализе) выражается в радианах. При x = 0 функция не определена.
Теорема. 
= 1 (первый замечательный предел).
Доказательство
Рассмотрим окружность радиуса R (рис. 1.12), OA = OC = R, тогда длина дуги АС равна: R×a, АВ = R×sina. Так как |AB| < ||, то 0 <… cosa = (1 – 2sin2) = 1 – 2×0 = 1. Вычислим теперь .Второй замечательный предел
Рассмотрим возрастающую последовательность: Для нее для любого натурального n. Если эта последовательность не является ограниченной, то она не имеет…Теорема 1 (достаточный признак существования предела последовательности)
Всякая возрастающая ограниченная сверху последовательность имеет предел.
Применим эту теорему для доказательства следующей теоремы.