рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Философия
- /
- Ортогональное планирование эксперимента
Реферат Курсовая Конспект
Ортогональное планирование эксперимента
Ортогональное планирование эксперимента - раздел Философия, ПЛАНИРОВАНИЕ И ОРГАНИЗАЦИЯ ЭКСПЕРИМЕНТА Структура Матрицы С Играет Важную Роль В Реа...
Структура матрицы С играет важную роль в реализации алгоритма определения коэффициентов аппроксимирующего полинома. Структура матрицы С зависит от выбора значений факторов в N опытах. Поэтому желательно особым образом выбирать значения факторов в опытах.
Элемент Сii на главной диагонали матрицы С (i-тая строка, i-тый столбец) представляется суммой квадратов значений i-того столбца сочетаний факторов матрицы Х в N опытах
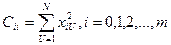
Элементы матрицы симметрично расположенные относительно главной диагонали равны между собой, то есть матрица С - симметричная.
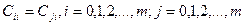 ;
;
где первый индекс указывает номер столбца матрицы Х, второй индекс - номер строки.
При этом
 .
.
Чтобы существовала матрица С-1, матрица С размера (1+m; 1+m) должна быть невырожденной, то есть ее определитель должен быть отличен от нуля. Это условие выполняется, если все m+1 столбцов матрицы Х линейно независимы. Кроме того, необходимо, чтобы число различных сочетаний факторов в матрице Х (число опытов N) должно быть не меньше чем m+1. Это условие исходит из того, что для определения m+1 коэффициента полинома необходимо не менее m+1 уравнений (опытов).
Полученные коэффициенты B позволяют сформировать уравнение функции отклика при m+1 членах уравнения. Если точность этого уравнения оказалась недостаточной, то требуется взять уравнение с большим числом членов и начать все заново так как все коэффициенты B оказываются зависимыми друг от друга. Это возникает при использовании пассивного эксперимента. Однако если целенаправленно использовать активный эксперимент и особым образом построить матрицу сочетаний факторов в опытах Х, использовать планирование эксперимента, то коэффициенты полинома определяются независимо друг от друга.
Стратегия применения планов заключается в принципе постепенного планирования – постепенного усложнения модели. Начинают с простейшей модели, находятся для нее коэффициенты, определяется ее точность. Если точность не удовлетворяет, то планирование и модель постепенно усложняются.
Задача планирования заключается в том как нужно строить матрицу Х, чтобы матрица С легко обращалась и коэффициенты B определялись независимо друг от друга. Эти требования выполняется если матрица С является диагональной, то есть все элементы расположенные не на главной диагонали матрицы равны нулю
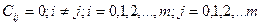
или
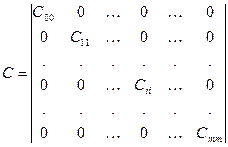
Тогда обратная матрица определяется как

В этом случае система уравнений распадается на m+1 независимых уравнения и коэффициенты полинома определяются как

Если учесть, что Сii определяется как сумма квадратов значений факторов
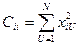 ,
,
то коэффициенты определяются как
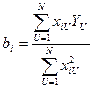
Требование выполнения условия Cij=Cji=0 заключается в выполнении условия
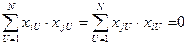
где i, j - номера столбцов в матрице Х; i=0,1,2,…,m; j=0,1,2,…,m при i≠j.
Каждый столбец матрицы Х можно представить в виде вектора
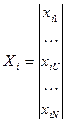 ,
, 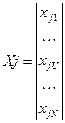
если 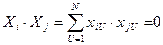 ,
,
то это означает что скалярное произведение двух векторов Хi и Хj равняется нулю, то есть векторы Хi и Хj - ортогональны.
Так как любое скалярное произведение двух различных столбцов в матрице Х должно быть равно нулю, то это условие называется условием ортогональности матрицы Х, а соответствующее планирование эксперимента (определение сочетаний факторов) называется ортогональным планированием.
Для ортогонального планирования при учете того что x0U=1, U=1,…,N

Таким образом, при ортогональном планировании сумма элементов любого столбца матрицы Х, кроме первого столбца должно быть равна нулю. Это правило используется при построении плана эксперимента, то есть при определении каким образом нужно менять значения факторов в опытах. Это правило показывает, что в ортогональном планировании при четном числе уровней, на которых фиксируется каждый фактор, то эти уровни должны быть симметрично расположены относительно центральной точки х=0, при нечетном числе уровней должна использоваться и центральная точка (рис.6).
Кроме свойства ортогональности план может обладать свойствам насыщенности, рототабельности и др. План является насыщенным, если общее число опытов N равняется числу неизвестных коэффициентов полинома m+1.
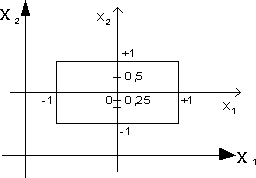
Рис. 6. Выбор уровней варьирования при ортогональном планировании
План называется рототабельным, если дисперсия отклика одинакова на одном расстоянии от центра плана при любом направлении в факторном пространстве. В упрощенном виде это означает, что все точки плана лежат на окружности (сфере, гиперсфере).
4. Планы полного факторного эксперимента 2n (планы ПФЭ 2n)
Алгоритм полного факторного эксперимента на двух уровнях с равным числом параллельных опытов. Исходные данные. Ставится задача определения локального оптимума на объекте исследования, для этого предполагается использовать математическую модель, полученную с помощью полного факторного эксперимента.
Выбирают факторы и выходную переменную, задают области определения факторов и выходной переменной
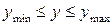 ;
;
 ; (1.126)
; (1.126)
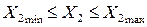 .
.
. . . . . . . . .
Кодирование. В области определения факторов выбирается точка Хi0, 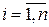 (нулевой уровень факторов), которая в предварительных исследованиях была признана наилучшей с точки зрения оптимума у. Задается интервал варьирования факторов ∆Хi. Определяются верхние и нижние уровни факторов:
(нулевой уровень факторов), которая в предварительных исследованиях была признана наилучшей с точки зрения оптимума у. Задается интервал варьирования факторов ∆Хi. Определяются верхние и нижние уровни факторов:
 ;
;
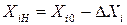 (1.127)
(1.127)
при условии, что  .
.
Кодируются факторы (переход к новой безразмерной системе координат x1, x2,…, xn):
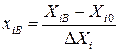 ;
;
(1.128)
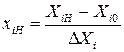 .
.
В новой системе координат факторы принимают значения + 1 и – 1 .
План эксперимента. План проведения эксперимента (матрица планирования) записывается в виде табл. 1.7.
Таблица 1.7. План эксперимента
| Номер опыта | x0 | План | Выходная переменная | |||||||
| x1 | x2 | … | xn | yu1 | yu2 | … | yum | 
| ||
| . . . N | +1 +1 . . . +1 | +1 –1 . . . –1 | +1 +1 . . . –1 | … … . . . … | +1 +1 . . . –1 | y11 y21 … yN1 | y12 y22 … yN2 | … … … … | y1m y2m … yNm |
 1 1
 2
… 2
…
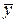 N N
|
В приведенном плане х0 – фиктивная переменная, равная единице; здесь также проводятся параллельные опыты – их число равно т в каждой строке матрицы планирования.
Пояснение. Предложенный план эксперимента обладает ортогональностью:
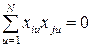 ,
, 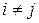 , i,
, i, 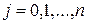 , (1.129)
, (1.129)
что соответствует следствию 2 [см. (1.107)] и вытекающему из него преимуществу независимого определения коэффициентов [см. (1.108) и (1.109)].
Как следствие (1.129) план эксперимента обладает симметричностью
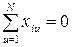 , (1.130)
, (1.130)
и нормировкой
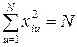 . (1.131)
. (1.131)
Ортогональные планы ПФЭ (для линейных моделей) обладают также ротатабельностью. Последнее предполагает равенство и минимальность дисперсий предсказанных значений выходной переменной для всех точек факторного пространства. По закону накопления ошибок для дисперсии предсказанных уравнением регрессии значений выходной переменной можно записать:
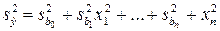 . (1.132)
. (1.132)
Из условий (1.112) вытекает, что дисперсии коэффициентов регрессии равны между собой, тогда
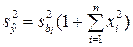 , (1.133)
, (1.133)
или с учетом того, что  (
(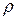 – радиус сферы)
– радиус сферы)
 . (1.134)
. (1.134)
Отсюда ясно, что дисперсия предсказанного значения выходной переменной зависит только от радиуса сферы. Это свойство ротатабельности эквивалентно независимости дисперсии выходной переменной от вращения координат в центре плана и оправдано при поиске оптимума градиентными методами. Интуитивно понятно, что исследователю удобно иметь дело с такой информацией, содержащейся в уравнении регрессии, которая равномерно «размазана» по сфере радиусом 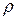 . Действительно, такое положение можно признать разумным, ибо с помощью уравнения регрессии будут предприниматься попытки предсказать положение еще неизвестных участков факторного пространства. Равноценность этих участков в смысле ошибки предсказания, по-видимому, является необходимой.
. Действительно, такое положение можно признать разумным, ибо с помощью уравнения регрессии будут предприниматься попытки предсказать положение еще неизвестных участков факторного пространства. Равноценность этих участков в смысле ошибки предсказания, по-видимому, является необходимой.
Расчет коэффициентов уравнения регрессии. Исходя из (1.108), (1.109) и (1.131) коэффициенты рассчитываются по уравнению
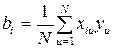 , i=0, 1, 2 ,…, n, (1.135)
, i=0, 1, 2 ,…, n, (1.135)
где  , (1.136)
, (1.136)
и окончательно
 , (1.137)
, (1.137)
где N – число строк матрицы планирования (число разных условий опыта); m – число параллельных опытов на каждой строке матрицы.
Построчные дисперсии по параллельным опытам на каждой строке матрицы рассчитываются по уравнению
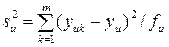 , (1.138)
, (1.138)
где  . (1.139)
. (1.139)
Проверка однородности дисперсий осуществляется по уравнениям (1.18) и (1.19) при условии mi=т, p=N индекс i заменяется индексом и.
Принятие решений. Если не выполняется условие (1.19), то гипотеза об однородности дисперсий отвергается и одними из решений являются увеличение числа параллельных опытов, изменение метода контроля выходной переменной, масштабирование выходной переменной.
Расчет ошибки опыта производится усреднением построчных дисперсий
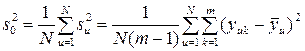 (1.140)
(1.140)
для числа степеней свободы
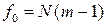 . (1.141)
. (1.141)
Оценка значимости коэффициентов регрессии производится расчетом t-критерия по формуле (1.90), расчетом дисперсий коэффициентов по формуле (1.119) с учетом (1.131) и оценкой по условию (1.91):
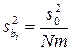 . (1.141,a)
. (1.141,a)
Принятие решений. Если для какого-то коэффициента условие (1.91) не выполняется, то соответствующий фактор можно признать незначимым и исключить его из уравнения. Однако рекомендуется помнить, что скорее всего полученная незначимость фактора является следствием неудачно выбранного (малого) интервала варьирования. Отсюда ясно, что более правильным является решение повторить эксперимент, расширив интервал варьирования для исследуемого фактора. Конечно, при этом число опытов, а значит и длительность эксперимента, возрастают. Иногда половину опытов сохраняют тем, что интервал варьирования расширяют только в одну сторону, другой же (верхний или нижний) уровень остается прежним.
Если фактор остался незначимым после повторения эксперимента и всех необходимых расчетов, то его (или их) отбрасывают и переходят к анализу адекватности уравнения.
Проверка адекватности уравнения регрессии осуществляется по формулам (1.92), (1.94), (1.95) с учетом параллельных опытов:
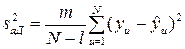 . (1.141,б)
. (1.141,б)
Поиск FT производится для степеней свободы fаД (1.93) и f0 (1.141).
Принятие решений. При выполнении условия (1.96), т.е. при неадекватной линейной модели, наиболее часто принимают решение об уменьшении интервалов варьирования факторов и повторении эксперимента. Такое решение хотя и уменьшает кривизну поверхности отклика, однако может привести к появлению незначимых коэффициентов. Очень эффективно включать в план эксперимента новый фактор из числа отсеянных ранее. Если условие (1.96) выполняется, то адекватный линейный полином можно использовать для решения различных задач (гл. 3).
1.5.2. Алгоритм ПФЭ с параллельными опытами в одной точке факторного пространства. Исходные данные не отличаются от алгоритма ПФЭ с одинаковым числом параллельных опытов (см. 1.5.1); так же проводится и кодирование.
План эксперимента строится с учетом априорной информации о хорошей воспроизводимости опытов, что не требует проверки однородности построчных дисперсий. Тогда для расчета ошибки опыта достаточно провести параллельных опытов (см. 1.5.1); так же проводится и пространства (без потери общности они могут быть поставленными в центре плана с координатами Х ={0,0, ...,0}, табл. 1.8).
Таблица 1.8. План эксперимента
| Номер опыта | x0 | План | Выходная переменная | |||
| x1 | x2 | … | xn | |||
| . . . N N+1 N+2 | +1 +1 . . . +1 +1 +1 | +1 –1 . . . –1 | +1 +1 . . . –1 | … … . . . … … … | +1 +1 . . . –1 | y1 y2 . . . yN y01 y02 |
| . . . | … | … | … | … | … | . . . |
| N+N0 | … | 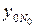
|
Расчет ошибки опыта производится по формуле
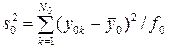 , (1.142)
, (1.142)
где 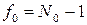 . (1.143)
. (1.143)
За исключением этапа проверки однородности дисперсий, все остальные этапы данного алгоритма совпадают с алгоритмом 1.5.1.
1.5.3. Алгоритм ПФЭ при неравном числе параллельных опытов.
Введение. На практике приходится сталкиваться с такими ситуациями, которые не позволяют при реализации эксперимента выдержать одинаковое число параллельных опытов по каждой строке матрицы планирования. Это происходит либо из-за случайных грубых нарушений условий эксперимента, когда измерение признается неудачным, а повторить его по каким-либо причинам не удается, либо вследствие неуверенности экспериментатора в «чистоте» опыта.
Последовательность обработки результатов эксперимента при неравном количестве параллельных опытов не нарушается, однако алгоритмы расчета меняются вследствие нарушения ортогональности матрицы планирования. Это приводит к изменению расчетных формул для коэффициентов регрессии и их ошибок, а также для дисперсии адекватности.
Исходные данные не отличаются от исходных данных алгоритма 1.5.1.
План эксперимента соответствует приведенному в табл. 1.7, однако в каждой строке число параллельных опытов ти может быть иным.
Расчет коэффициентов уравнения регрессии. Вследствие неортогональности матрицы планирования расчет коэффициентов регрессии осуществляется по методу наименьших квадратов. Лучше всего использовать матричную форму записи и стандартные программы ЭВМ – обращение матриц, транспонирование, расчет детерминанта матриц и т. д. [см. 1.4.1, формула (1.103)].
Расчет ошибки опыта. Рассчитываются построчные дисперсии по формулам (1.138) и (1.139).
При усреднении построчных дисперсий пользуются средневзвешенными значениями дисперсий, взятыми с учетом числа степеней свободы fu, для u-ой строки матрицы планирования:
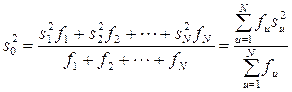 . (1.144)
. (1.144)
Проверка однородности дисперсий. При неравном числе параллельных опытов для проверки однородности дисперсий используется критерий Бартлета. Для этого рассчитывается величина Ар:
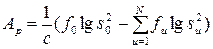 ; (1.145)
; (1.145)
 , (1.146)
, (1.146)
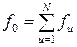 , (1.147)
, (1.147)
где f0 – число степеней свободы; N – число сравниваемых дисперсий (здесь их число равно числу строк матриц).
Принятие решений. Бартлет доказал, что рассчитанная величина Ар приближается к  – распределению с N – 1 степенями свободы. Тогда, если выполняется неравенство
– распределению с N – 1 степенями свободы. Тогда, если выполняется неравенство
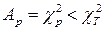 ,
,  , (1.148)
, (1.148)
то дисперсии признаются однородными.
Замечание. Критерий Бартлета базируется на нормальном распределении случайной величины уи. Поэтому проверка нормальности закона распределения уи весьма желательна.
Учитывая сложность применения критерия Бартлета при неодинаковом числе параллельных опытов, практически удобно использовать критерий Фишера. Для этого составляется отношение максимальной построчной дисперсии к минимальной:
 . (1.149)
. (1.149)
Очевидно, что если выполнять условие
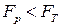 (1.150)
(1.150)
при 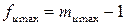 ,
, 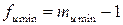 и заданном уровне значимости q (т.е. максимальная и минимальная дисперсии отличаются незначимо), то и остальные дисперсии будут отличаться незначимо. Таким образом, гипотезу об однородности дисперсий можно признать правомерной при выполнении условия (1.150).
и заданном уровне значимости q (т.е. максимальная и минимальная дисперсии отличаются незначимо), то и остальные дисперсии будут отличаться незначимо. Таким образом, гипотезу об однородности дисперсий можно признать правомерной при выполнении условия (1.150).
Проверка значимости коэффициентов регрессии не отличается от произведенной выше при равном числе параллельных опытов. Следует отметить, что смысл проверки несколько меняется вследствие неортогональности матрицы планирования, что приводит к появлению недиагональных элементов в матрице 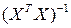 .Однако по значениям они обычно невелики и поэтому критерий Стьюдента можно использовать как средство ранжирования коэффициентов регрессии в соответствии с формулами (1.90), (1.91), числом степеней свободы f0 (1.147) и заданным уровнем значимости.
.Однако по значениям они обычно невелики и поэтому критерий Стьюдента можно использовать как средство ранжирования коэффициентов регрессии в соответствии с формулами (1.90), (1.91), числом степеней свободы f0 (1.147) и заданным уровнем значимости.
Принятие решений не отличается от предыдущих алгоритмов.
Проверка адекватности уравнения регрессии. Расчет дисперсии адекватности осуществляется по формуле
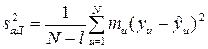 . (1.151)
. (1.151)
Физический смысл формулы таков: различию между экспериментальным и расчетным значениями выходной переменной придается тем больший вес, чем большее число опытов реализуется. Здесь ти фактически является весовым коэффициентом. Для проверки адекватности используется критерий Фишера в соответствии с (1.95) и (1.96).
Принятие решений не отличается от предыдущих алгоритмов.
1.5.4. Алгоритм ПФЭ с расчетом коэффициентов взаимодействийфакторов. Введение. Ранее уже упоминалось, что цель ПФЭ – получение адекватной линейной модели, которую предполагается использовать для оптимизации объекта исследования. В задачах интерполяции же математическая модель должна адекватно описывать объект в области эксперимента и потому может быть нелинейной. Планы ПФЭ, с одной стороны, позволяют достаточно просто рассчитать коэффициенты при взаимодействиях факторов и, если они значимы, использовать полученную модель для интерполяционных целей. С другой стороны, значимость коэффициентов при взаимодействиях факторов сразу же позволяет сделать вывод о неадекватности линейной модели.
Исходные данные в отличие от 1.5.1 пополняются условием необходимости расчета коэффициентов при взаимодействиях факторов, т.е. ищется модель в виде

(1.152)
 .
.
План эксперимента дополняется расчетными столбцами xi xj. Например, план ПЭФ 23 приведен в табл. 1.9.
Таблица 1.9. План эксперимента
| Номер опыта | x0 | План | Выходная переменная | |||||
| реализуемый | расчетный | |||||||
| x1 | x2 | x3 | x1x2 | x1x3 | x2x3 | |||
| +1 –1 +1 +1 +1 +1 +1 +1 | +1 +1 +1 –1 +1 –1 +1 –1 | +1 +1 –1 –1 +1 +1 –1 –1 | +1 +1 +1 +1 –1 –1 –1 –1 | +1 –1 –1 +1 +1 –1 –1 +1 | +1 –1 +1 –1 –1 –1 +1 –1 | +1 +1 –1 –1 –1 –1 +1 +1 | y1 y2 y3 y4 y5 y6 y7 y8 |
Расчет коэффициентов проводится по уравнению
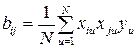 , i=1, 2, …, n,
, i=1, 2, …, n, 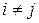 . (1.153)
. (1.153)
Остальные этапы не отличаются от приведенных в алгоритме 1.5.1.
Замечание 1. В задачах оптимизации необходимо, чтобы все bij были незначимы, а в задачах интерполяции наоборот – значимы (хотя бы некоторые). Поэтому для задач оптимизации всегда проводят расчет bij и используют их для проверки адекватности модели.
Замечание 2. Существует еще одна проверка нелинейности модели оценкой гипотезы о равенстве нулю суммы коэффициентов при квадратичных членах. С этой целью в центре плана ставят несколько опытов, определяют среднее 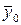 и вычисляют разность
и вычисляют разность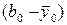 , которая и является оценкой суммы коэффициентов при квадратичных членах.
, которая и является оценкой суммы коэффициентов при квадратичных членах.
Действительно, свободный член b0, который рассчитывают по уравнению:
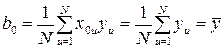 , (1.154)
, (1.154)
является совместной оценкой  и
и 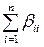 :
:
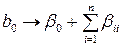 , (1.155)
, (1.155)
где β0 – свободный член уравнения регрессии по генеральной совокупности экспериментальных данных; βii – коэффициенты при 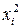 также по генеральной совокупности.
также по генеральной совокупности.
Это положение вытекает из идентичности столбцов матрицы планирования при х0 и 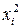 (они все равны + 1). Тогда разность
(они все равны + 1). Тогда разность  может в какой-то мере служить оценкой кривизны поверхности отклика выходной переменной. Значимость этой разницы проверяют по условию:
может в какой-то мере служить оценкой кривизны поверхности отклика выходной переменной. Значимость этой разницы проверяют по условию:
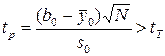 , (1.156)
, (1.156)
где s0 – среднеквадратичное отклонение ошибок опыта; N – число опытов; tT – табличное значение критерия Стьюдента для числа степеней свободы дисперсии 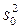 и уровня значимости q.
и уровня значимости q.
Выполнение условия (1.156) свидетельствует о значимости квадратичных членов, и требуется их введение в интерполяционное уравнение или уменьшение интервалов варьирования факторов для получения адекватной линейной модели.
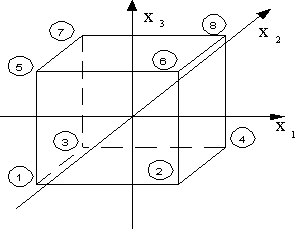
Рис. 32. Геометрическое отображение плана ПФЭ 23 в факторном пространстве
5.5. Планы дробного факторного эксперимента (планы ДФЭ)
При многофакторном эксперименте, особенно когда число факторов больше шести (n > 6), число опытов планов ПФЭ 2n (N = 2n) становится чрезмерным. Если нам не требуется определение всех коэффициентов неполного квадратичного полинома, то переходят к дробному факторному эксперименту (ДФЭ) – части полного факторного эксперимента.
Число необходимых опытов в условиях линейной модели существенно сокращается при проведении дробных факторных экспериментов (дробных реплик от ПФЭ). В качестве реплики обычно используется полный факторный эксперимент для меньшего числа факторов. При этом вычисление коэффициентов уравнения и оценка их значимости проводится так же, как и в рассмотренных выше примерах ПФЭ 22 и 23. Число опытов в дробной реплике должно быть больше или равно числу неизвестных коэффициентов в уравнении регрессии.
Алгоритм дробного факторного эксперимента (ДФЭ). Введение. Полный факторный эксперимент является весьма эффективным средством получения математической модели исследуемого объекта особенно при числе факторов n>3. Однако увеличение числа факторов приводит к резкому увеличению числа опытов. Так, ПФЭ 26 требует постановки 64 опытов, а 27 – 128 опытов. Конечно, точность модели при увеличении числа опытов также возрастает, однако, известно, что увеличение числа опытов приводит к большим затратам средств и времени.
Практика показывает, что для получения достаточно точных оценок коэффициентов регрессии можно обойтись малым количеством опытов, вводя понятие дробного факторного эксперимента (или дробных реплик), который представляет собой некоторую часть ( и т.д.) от полного факторного эксперимента (см. 1.1.3).
и т.д.) от полного факторного эксперимента (см. 1.1.3).
Сокращение числа опытов влечет за собой появление корреляции между некоторыми столбцами матрицы планирования. Это обстоятельство не позволяет раздельно оценивать эффект факторов и эффекты взаимодействия. Получаются так называемые смешанные оценки.
Определения. Для дробных реплик используют специальные алгебраические соотношения, облегчающие выявление смешанных эффектов. Они называются генерирующими соотношениями и определяющими контрастами.
Генерирующим называется соотношение, которое показывает, какое из взаимодействий принято незначимым, а потому заменено в матрице планирования новой независимой переменной. Так, рассмотренный в табл.1.10 план типа  задавался генерирующим соотношением
задавался генерирующим соотношением
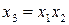 .
.
Таблица 1.10. План эксперимента
| Номер опыта | x0 | План | Выходная переменная | ||
| x1 | x2 | x3=x1 x2 | |||
| +1 +1 +1 +1 | +1 –1 +1 –1 | +1 +1 –1 –1 | +1 –1 –1 +1 | y1 y2 y3 y4 |
С генерирующими соотношениями можно производить алгебраические операции: умножать обе части равенства на любые эффекты – линейные и определенные взаимодействия. При этом, если фактор входит в уравнение в квадрате или в другой четной степени, то он заменяется единицей  . Умножив генерирующее соотношение для плана
. Умножив генерирующее соотношение для плана  на х3:
на х3:
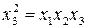 ,
,
или, учитывая вышесказанное, получим
 .
.
Это и есть определяющий контраст – соотношение, которое задает элементы первого столбца матрицы (как известно, элементы первого столбца матрицы равны 1).
План эксперимента. Зная определяющий контраст, можно найти соотношения, задающие все смешанные оценки для данной дробной реплики. Для этого определяющий контраст умножается на каждый фактор. В рассматриваемом примере для первой полуреплики от плана 23 смешанные оценки коэффициентов регрессии задаются следующими соотношениями:
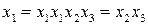 ;
;
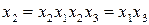 ;
;
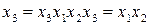 ,
,
что соответствует оценкам
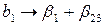 ;
;  ;
;  .
.
Замечание. Эффективность системы смешивания факторов и взаимодействий факторов определяется так называемой разрешающей способностью матрицы. Она считается максимальной, если линейные эффекты смешаны с эффектами взаимодействия, наибольших по числу факторов в него входящих. Так, при выборе полуреплики 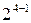 возможны восемь решений
возможны восемь решений
1. 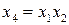 ; 5.
; 5. 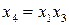 ;
;
2. 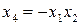 ; 6.
; 6. 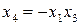 ;
;
3. 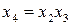 ; 7.
; 7.  ;
;
4. 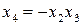 ; 8.
; 8. 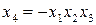 .
.
Согласно принятому определению, наибольшая разрешающая способность у реплик 7 и 8, они называются главными. При наличии априорной информации и значимости взаимодействий факторов можно разработать наилучшую систему смешивания оценок. Если эти сведения отсутствуют, то выбирают реплику с наибольшей разрешающей способностью, поскольку тройные взаимодействия обычно менее важны, чем двойные.
Остальные этапы алгоритма – расчет коэффициентов регрессии и статистический анализ уравнения – не отличаются от приведенных выше.
1.6. Факторный эксперимент второго порядка
Введение. Задачей факторного эксперимента второго порядка является проведение оптимального плана исследований, получение нелинейной модели и ее статистический анализ. Модель применяется для поиска координаты оптимума и может использоваться для целей интерполяции и экстраполяции.
Обычно факторный эксперимент второго порядка используется для описания существенно нелинейных объектов полиномом
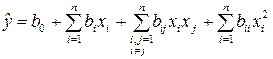 . (1.157)
. (1.157)
Пояснение. Построить планы, по которым можно получить модель в виде (1.157) с помощью ранее рассмотренных алгоритмов не удается хотя бы потому, что условие ортогональности в столбцах матрицы не выполняется (сумма элементов столбцов не равна нулю). Также требуется поставить большое число опытов. Очевидно, что планирование на трех уровнях Зп неэкономично и потому предложено дополнить план ПФЭ 2п определенными точками факторного пространства так, чтобы выполнялось условие ортогональности или ротатабельности, но при этом число опытов таких планов было меньшим, чем ПФЭ Зп:
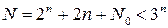 , (1.158)
, (1.158)
где каждое слагаемое определяет число опытов ПФЭ 2п, число «звездных» и число нулевых опытов (в центре плана). Из формулы (1.158) вытекает, что предлагаемые планы (при п>2) экономичнее планов на трех уровнях (обычно N0 = 1).
Большим преимуществом таких планов является то, что их можно получать из планов 2п. Для построения используется план 2n, линейная модель по которому при поиске области оптимума оказалась неадекватной. Все проведенные эксперименты остаются, а план пополняется определенным количеством специально подобранных «звездных» точек. Отметим, что дробная реплика предыдущего плана в новом плане дополняется до полного факторного эксперимента, если n≤4; при n>4 возможно использование дробных реплик. Организованные таким образом планы называются центральными и композиционными. Общий вид плана приведен в табл. 1.11.
Таблица 1.11. План эксперимента
| Номер опыта | x0 | План | Выходная переменная | ||||
| x1 | x2 | x1 x2 | 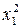
| 
| |||
| +1 +1 +1 +1 +1 +1 +1 +1 +1 | +1 +1 –1 –1 +α –α | +1 –1 +1 –1 +α –α | +1 –1 –1 +1 |
+1
+1
+1
+1
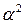
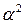
|
+1
+1
+1
+1
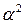
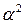
| y1 y2 y3 y4 y5 y6 y7 y8 y9 |
Выбор плеча «звездных» точек и числа нулевых точек зависит от критерия оптимальности плана. В инженерной практике широко применяются ортогональные и ротатабельные планы второго порядка.
1.6.1. Алгоритм ортогонального плана второго порядка (ЦКОП). Исходные данные. Имеется план ПФЭ 2n. Математическая модель, полученная по этому плану, неадекватная. Условия (1.126) остаются прежними.
Кодирование. Для получения ортогональных планов второго порядка необходимо провести некоторое преобразование столбцов квадратичных переменных и столбца х0. Это вызвано неортогональностью указанных столбцов матрицы планирования (см. табл. 1.11), поскольку
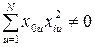 ; (1.159)
; (1.159)
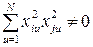 . (1.160)
. (1.160)
Неравенства справедливы, поскольку значения в столбцах х0 и 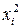 всегда положительны. Заметим, что в ортогональных планах на количество нулевых точек обычно не накладывают никаких условий, поэтому N0 принимают равным единице.
всегда положительны. Заметим, что в ортогональных планах на количество нулевых точек обычно не накладывают никаких условий, поэтому N0 принимают равным единице.
Для ортогональности исходного плана введем преобразование
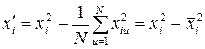 , (1.161)
, (1.161)
тогда
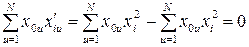 .
.
Если приравнять недиагональный элемент ковариционной матрицы 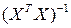 нулю и решить его относительно α, то можно найти его значение, организующее ортогональность столбцов
нулю и решить его относительно α, то можно найти его значение, организующее ортогональность столбцов 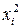 (значения α для различных п приведены в табл.1.12).
(значения α для различных п приведены в табл.1.12).
Таблица 1.12. Величина плеча для ортогональных планов второго порядка
| Наименование элементов плана | Число независимых факторов | |||
| Ядро плана | 22 | 23 | 24 | 25-1 |
| α | 1,00 | 1,215 | 1,414 | 1,547 |
План эксперимента. Ортогональная матрица композиционного плана для n=2 приведена в табл. 1.13. Значения 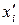 находятся по формуле (1.161)
находятся по формуле (1.161)
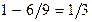 , или
, или 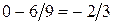 .
.
Таблица 1.13. План эксперимента
| Номер опыта | x0 | План | Расчетная матрица | Выходная переменная | |||
| x1 | x2 | x1 x2 | 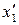
| 
| |||
| +1 +1 +1 +1 +1 +1 +1 +1 +1 | +1 +1 –1 –1 +1 –1 | +1 –1 +1 –1 +1 –1 | 1/3 1/3 1/3 1/3 1/3 1/3 –2/3 –2/3 –2/3 | 1/3 1/3 1/3 1/3 1/3 1/3 –2/3 –2/3 –2/3 | 1/3 1/3 1/3 1/3 –2/3 –2/3 1/3 1/3 –2/3 | y1 y2 y3 y4 y5 y6 y7 y8 y9 |
Ортогональная матрица композиционного плана для п=3 приведена в табл. 1.14. Значения 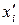 находят по формуле (1. 161)
находят по формуле (1. 161)
 или
или  .
.
Расчет коэффициентов регрессии осуществляется в соответствии с методом наименьших квадратов (см. 1.4.1). Коэффициенты и их дисперсии можно также рассчитывать по формулам
 ; (1.162)
; (1.162)
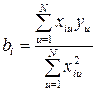 ; (1.163)
; (1.163)
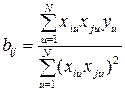 ; (1.164)
; (1.164)
 ; (1.165)
; (1.165)
Таблица 1.14 План эксперимента
| Номер опыта | x0 | План | Расчетная матрица | Выходная переменная | |||||||
| x1 | x2 | x3 | 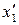
| 
| 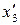
| x1 x2 | x1 x3 | x2 x3 | |||
| +1 +1 +1 +1 +1 +1 +1 +1 +1 +1 +1 +1 +1 +1 +1 | +1 –1 +1 –1 +1 –1 +1 –1 1,215 –1,215 | +1 +1 –1 –1 +1 +1 –1 –1 1,215 –1,215 | +1 +1 +1 +1 –1 –1 –1 –1 1,215 –1,215 | 0,27 0,27 0,27 0,27 0,27 0,27 0,27 0,27 0,746 0,746 –0,73 –0,73 –0,73 –0,73 –0,73 | 0,27 0,27 0,27 0,27 0,27 0,27 0,27 0,27 –0,73 –0,73 –0,746 –0,746 –0,73 –0,73 –0,73 | 0,27 0,27 0,27 0,27 0,27 0,27 0,27 0,27 –0,73 –0,73 –0,73 –0,73 0,746 0,746 –0,73 | +1 –1 –1 +1 +1 –1 –1 +1 | +1 –1 +1 –1 –1 +1 –1 +1 | +1 +1 –1 –1 –1 –1 +1 +1 | y1 y2 y3 y4 y5 y6 y7 y8 y9 y10 y11 y12 y13 y14 y15 |
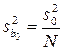 ; (1.166)
; (1.166)
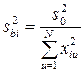 ; (1.167)
; (1.167)
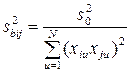 ; (1.168)
; (1.168)
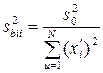 , (1.169)
, (1.169)
где 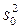 – ошибка опыта, известная по полному факторному эксперименту.
– ошибка опыта, известная по полному факторному эксперименту.
Дисперсия величины b0 оценивается по уравнению
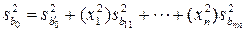 . (1.170)
. (1.170)
Оценка значимости коэффициентов проводится по критерию Стьюдента (см. (1.90)), а решения принимаются в соответствии с (1.91). Благодаря ортогональности плана после отбрасывания незначимых коэффициентов оставшиеся не пересчитываются.
Проверка адекватности уравнения регрессии осуществляется расчетом SOCT сначала по формуле (1.92) и далее по формулам (1.93), (1.94), (1.95).
Значение 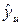 определяется по уравнению
определяется по уравнению

 (1.171)
(1.171)
или
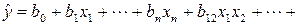
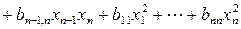 . (1.172)
. (1.172)
Переход от (1. 171) к (1. 172) осуществляется расчетом величины свободного члена по уравнению
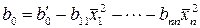 , (1.173)
, (1.173)
где
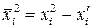 .
.
Принятие решений осуществляется в соответствии с (1.96).
Кодирование и основы построения плана. Построение ротатабельности планов второго порядка – сложная математическая задача, требующая доказательства нескольких теорем. Воспользуемся результатами исследований, где предлагается условия ротатабельности задавать уравнениями

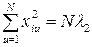 , i = 1, 2, …, n;
, i = 1, 2, …, n;
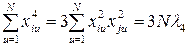 (1.174)
(1.174)
(i j, i, j = 1, 2, …, n),
j, i, j = 1, 2, …, n),
где n – число факторов; N – число опытов;  и
и 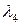 – некоторые константы, связанные неравенством
– некоторые константы, связанные неравенством
 , (1.175)
, (1.175)
которое является условием невырожденности информационной матрицы (ХТХ).
Если ввести несколько точек на сфере с нулевым радиусом, т.е. несколько точек в центре плана N0, то можно рассчитать параметр
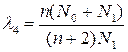 , (1.176)
, (1.176)
где 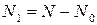 , и усилить неравенство (1.175), поскольку
, и усилить неравенство (1.175), поскольку
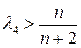 . (1.177)
. (1.177)
«Звездные» точки ротатабельности планов строят на осях координат факторов с величиной звездного плеча 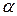 , рассчитанного по формуле
, рассчитанного по формуле
 , (1.178)
, (1.178)
а для дробного факторного эксперимента
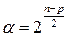 , (1.179)
, (1.179)
где п – число факторов; р – определяет дробность реплики (р=1 – полуреплика, р = 2 – четверть реплики и т. д.).
Выбор 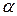 , числа «звездных» и числа нулевых точек удобно делать по табл. 1.15.
, числа «звездных» и числа нулевых точек удобно делать по табл. 1.15.
Таблица 1.15. Параметры ротатабельных планов второго порядка
| Наименование элементов плана | ПФЭ 2n | ДФЭ 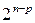
| |||
| n=2 | n=3 | n=4 | n=5 | n=5 | |
Число опытов в ядре матрицы
Число «звездных» точек
Число нулевых точек
Значение 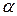
|
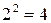 1,414
1,414
|
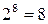 1,682
1,682
|
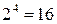 2,000
2,000
|
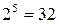 10
2,378 10
2,378
|
 2,000
2,000
|
План эксперимента совпадает с ЦКОП, но при других значениях параметров 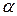 , N0 (см. табл. 1.11).
, N0 (см. табл. 1.11).
Расчет коэффициентов регрессии. Обработка результатов реализации планов второго порядка требует в целом значительной вычислительной работы и лучше всего ее проводить на ЭЦВМ по формуле (1.103).
Специфический характер матрицы (ХТХ) для ЦКРП позволяет получить общие формулы для расчета коэффициентов. Основная задача вычислительной машины в этом случае – выдача на печать следующих элементов обращенной матрицы:
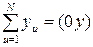 ,
, 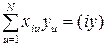 ;
;
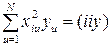 ,
, 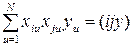 . (1.180)
. (1.180)
Если обозначить
 ;
;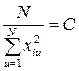 , (1.181)
, (1.181)
то с учетом (1.176), (1.180) и (1.181) коэффициенты регрессии можно определить по формулам
 ; (1.182)
; (1.182)
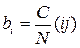 ; (1.183)
; (1.183)
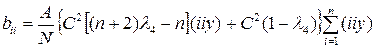 ; (1.184)
; (1.184)
 . (1.185)
. (1.185)
Для n=3 приведенные формулы имеют вид
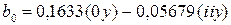 ; (1.186)
; (1.186)
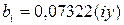 ; (1.187)
; (1.187)
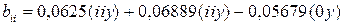 ; (1.188)
; (1.188)
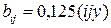 . (1.189)
. (1.189)
Оценка значимости коэффициентов регрессии. Дисперсии для коэффициентов регрессии рассчитываются по формулам
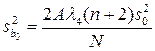 ; (1.190)
; (1.190)
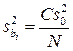 ; (1.191)
; (1.191)
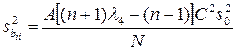 ; (1.192)
; (1.192)
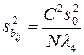 , (1.193)
, (1.193)
где 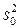 – дисперсия опыта.
– дисперсия опыта.
Оценка значимости коэффициентов регрессии проводится так же, как и в ЦКОП.
Принятие решений. Если незначимым оказался один из квадратичных эффектов, то после его исключения уравнение регрессии необходимо посчитать заново (это связано с неортогональностью квадратичных столбцов матрицы планирования). Остальные незначимые коэффициенты упускаются без пересчета уравнения.
Проверка адекватности уравнения регрессии. Преобразования ротатабельного плана несколько изменили формулы расчета дисперсий.
Так, сумму квадратов отклонений в центре плана можно подсчитать по формуле
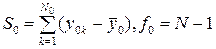 , (1.194)
, (1.194)
где 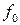 – число степеней свободы этой суммы; k= 1, 2, …, N0.
– число степеней свободы этой суммы; k= 1, 2, …, N0.
Дисперсия опыта получается делением суммы (1.194) на 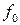 :
:
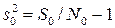 . (1.195)
. (1.195)
Остаточная сумма квадратов вычисляется так:
 ,
, 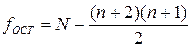 , (1.196)
, (1.196)
или
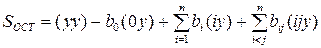 . (1.197)
. (1.197)
Сумма квадратов Sад, оценивающая адекватность модели, подсчитывается по формуле
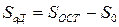 ,
, 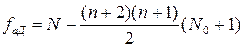 . (1.198)
. (1.198)
Расчетное значение критерия Фишера, как и ранее, формируют как отношение дисперсии адекватности к Дисперсии опыта (1.94) и (1.95) и сравнивают с табличными значениями FT для степеней свободы 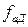 и
и 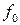 по известным равенствам (см. (1.96)).
по известным равенствам (см. (1.96)).
Принятие решении. Если условие (1.96) не выполняется, то нелинейная модель, полученная по плану ЦКРП, неадекватна. В этом случае требуется изменение порядка полинома (переход к полиному третьего порядка), добавление факторов в уравнение регрессии или тщательный анализ ошибок в эксперименте (получающихся, например, вследствие временного дрейфа).
5.6. Насыщенные планы первого порядка
Насыщенным планом первого порядка – называется план, содержащий n+1 точку (опыт). Например, при n = 4, N=n + 1 = 5.
То есть полином формируется в виде
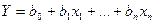 .
.
Таким образом, насыщенный план – это предельно минимальный случай плана ДФЭ. Такие планы называются симплекс-планы. Для симплекс-плана при n = 1 N = 2 его геометрическое изображение представлено на рис. 34, а; при n=2, N=3 – на рис. 11, б; при n=3, N=4 – на рис. 11, в. Симплекс-планы обычно используются на стадии предварительного исследования.
– Конец работы –
Эта тема принадлежит разделу:
ПЛАНИРОВАНИЕ И ОРГАНИЗАЦИЯ ЭКСПЕРИМЕНТА
Государственное образовательное учреждение... Высшего профессионального образования... МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕКСТИЛЬНЫЙ...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Ортогональное планирование эксперимента
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов