Квантовая проводимость. Формула Ландауэра.

Для самого простого описания эффектов квантовой проводи­мости удобно рассмотреть одномерную мезоскопическую по­лупроводниковую структуру, типа квантовой проволоки. Если такая проволока является достаточно короткой (т. е. ее длина меньше среднего свободного пробега электрона в рассматрива­емом веществе), то движение электронов будет происходить без рассеяния, и перенос будет носить баллистический характер. Предположим, что, как показано на рис. 6.11, такая кванто­вая проволока идеальными контактами (т. е. такими, в кото­рых полностью отсутствуют процессы рассеяния) соединена с двумя резервуарами, характеризующимися уровнями Ферми Е_F1 и Е_F2, между которыми приложено слабое напряжение V для обеспечения протекания тока через проволоку. В результате между резервуарами возникает разность потенциалов еV, рав­ная (Е_F1 - Е_F2).

Рис. 6.11. Схематическое представление одномерной мезоскопической системы, используемое для вывода формулы Ландауэра.

Величина протекающего при этом по проволоке тока I равна произведению концентрации электронов (которую можно определить по функции плотности состояний п_1D(Е) в интервале энергий еV) на скорость электронов v(Е) и единич­ный заряд:

I = eп_1D(Е)v(E)eV. (6.10)

Подставляя в это выражение формулу (4.21) для плотности состояний п_1D(Е) (из формулы выбрасывается только коэффи­циент 2, поскольку в рассматриваемой системе электроны могут двигаться лишь в одном направлении), можно легко получить для тока выражение

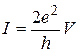, (6.11)

которое, что довольно интересно, оказывается не зависящим от скорости носителей. Проводимость G≡ (I/V) при этом равна

. (6.12)

Стоит отметить также, что (в отличие от классической про­водимости, обратно пропорциональной длине проводника) проводимость квантовой проволоки вообще никак не зависит от ее длины. Отношение

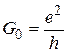(6.13)

называется квантовой единицей проводимости, а соответствую­щее обратное отношение

kW (6.14)

называется квантовым сопротивлением и может быть измере­но экспериментально. Поскольку отношение 2е²/h используется в теории очень часто, его иногда называют также фундамен­тальной проводимостью.

Все приведенные формулы для квантовой проводимости и сопротивления были получены на основе чрезвычайно прос­той, одномерной мезоскопической модели, однако сам факт квантования классических физических параметров (типа про­водимости и сопротивления) в физике мезоскопических сис­тем имеет фундаментальное значение. Для рассмотрения более сложных систем мы постараемся обобщить полученные резуль­таты. Один из вариантов такого обобщения, предложенный в следующем разделе, состоит в использовании наноструктур с большим числом соединений (а не двух, как в случае одно­мерной системы). Еще вариант обобщения результатов связан с учетом энергетических подзон в рассматриваемых низко­размерных полупроводниках. Если концентрация электронов или их энергия достаточно велики, в перенос могут вовлекаться электроны подзон, лежащих выше первого уровня квантования.

Для квантовых проволок такие подзоны (каналы, по термино­логии квантового переноса) возникают из поперечных состояний. Предполагая наличие нескольких каналов, можно представить, что электроны могут инжектироваться из контактов в любой канал (или моду) т, поступать в мезоскопическую струк­туру, а затем, после взаимодействия с рассеивающим центром, возникать в другом канале — п. Такие электроны будут вносить свой вклад в полную или общую проводимость системы, равный произведению кванта проводимости 2е²/h на квантово-мехническую вероятность перехода |t_mn|², соответствующую инжекции электронов в канал т и их переходу в другой канал п (отметим, что в такой формулировке вероятность перехода выражается через амплитуды или вероятности пропускания t_mn волновых функций электрона). Полная проводимость в этом случае может быть полу­чена суммированием процессов по всем каналам, т. е.

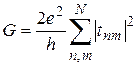, (6.15)

где N — полное число каналов, участвующих в рассматрива­емых процессах проводимости. Уравнение (6.15), называемое формулой Ландауэра, может рассматриваться как обобщение уравнения (6.12) для мезоскопической системы с двумя контак­тами и большим числом каналов.

При изучении процессов квантового переноса часто исполь­зуются наноструктуры, состоящие из сужений внутри двумерной системы. В качестве примера можно привести показанную на рис. 6.12 структуру, в которой движение электронов в двумерной гетероструктуре управляется расщепленным затвором. Исполь­зование электрода с такой специальной формой позволяет при приложении напряжения вследствие формируемого распределе­ния потенциала ограничить движение электронов в плоскости двумерной системы и заставить их двигаться в очень малой ква­зиодномерной области. Такие структуры называют квантовым точечным контактом (QРС) или даже электронным волноводом, по аналогии с привычными волноводами в радиофизике.

На рис. 6.12 представлены результаты первого эксперимента по обнаружению квантовой проводимости, проведенного Визом и другими в 1988 г. на квантовом точечном контакте (форма которого приведена на врезке), образованном в квантовой гете­роструктуре АlGаАs/GаАs. Легко заметить, что с ростом прило­женного напряжения экспериментально измеренная квантовая проводимость меняется скачками (квантуется) с шагом, равным упомянутой выше фундаментальной проводимости 2е²/h. Кванто­вание явно следует из уравнения (6.15), в котором коэффициенты пропускания приближаются к единице вследствие очень низких скоростей процессов рассеяния, что заведомо справедливо для квантовых точечных контактов. При этом экспериментальное на­блюдение горизонтальных участков вольт-амперной характеристики представляет собой часто сложную задачу, так как эта ломаная линия «сглаживается» в результате многих побочных процессов: влияния неупругого рассеяния, конечного сопротивления кон­тактов, наличия примесных атомов, шероховатости поверхности и т. д.

Рис. 6.12. Зависимость квантовой проводимости от напряжения на управляющем электроде (форма которого приведена на врезке) при 0,6 К для квантовых точечных контактов, создаваемых в гетероструктуре АlGаАs/GаАs.

В результате указанных факторов неточность определения экспериментально измеряемых значений ступенек на кривой про­водимости может достигать нескольких процентов, что и показано на рисунке. С другой стороны при наложении сильных магнитных полей, в силу столь же объективных причин, точность измерения высоты сту­пенек на кривой проводимости повышается на несколько поряд­ков и возрастает до 10⁶ раз! Именно по этой причине квантовый эффект Холла, находит множество применений в метрологии и технике точных измерений.