рефераты конспекты курсовые дипломные лекции шпоры
Реферат Курсовая Конспект
Рассеяние частиц на потенциальной ступеньке.
Рассеяние частиц на потенциальной ступеньке. - Лекция, раздел Философия, ЛЕКЦИЯ №1 ФУНДАМЕНТАЛЬНЫЕ ЯВЛЕНИЯ. ПОЛУПРОВОДНИКОВЫЕ СТРУКТУРЫ И ИХ КЛАССИФИКАЦИЯ Проведем Анализ Системы, В Которой Частицы, Испускаемые Источником, Удаленны...
Проведем анализ системы, в которой частицы, испускаемые источником, удаленным на большое расстояние, рассеиваются на той или иной преграде, уходя после этого в бесконечность.
Простейшей моделью данной задачи, соответствующей случаю рассеяния на потенциальном рельефе с большим масштабом неоднородности, является рассеяние частицы на потенциальной ступеньке (прямоугольном потенциальном барьере бесконечной ширины)
 (1)
(1)
где U0 = const (рис. 2.1, а).

|
| Рис. 2.1. Энергетическая диаграмма (a) и зависимость коэффициента отражения R от Е/U0 (б) для прямоугольной ступеньки. |
Исследуем особенности поведения частицы в таком потенциальном рельефе. Будем полагать, что источник частиц находится далеко слева (при x®-¥), а испускаемые им частицы движутся слева направо.
Поскольку задача стационарная (высота барьера не зависит от времени), отыскание состояний движения частицы сводится к решению стационарного одномерного уравнения Шредингера
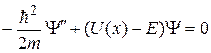 , (2)
, (2)
здесь т - масса частицы; Е - полная энергия частицы.
В данном случае уравнение (2) удобно решать отдельно для областей x < 0 и x > 0. В области х < 0 (на рис. 2.1, а область 1), где U(х) = 0, (2) принимает вид уравнения для свободной частицы, а его общее решение
 , (3)
, (3)
где
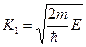 . (4)
. (4)
Если учесть, что в случае стационарных состояний волновая функция гармонически зависит от времени, то Y1 представляет собой суперпозицию падающей и отраженной волн де Бройля. Таким образом, А1 является амплитудой волны, распространяющейся от источника к потенциальной ступеньке (падающие на ступеньку частицы), а В1 - амплитудой рассеянной волны, распространяющейся назад к источнику (отраженные от ступеньки частицы).
В области х > 0 (область 2) уравнение (2) принимает вид
 . (5)
. (5)
Характер решения уравнения (5) определяется соотношением между энергией падающей частицы Е, задаваемой источником, и высотой потенциальной ступеньки U0.
В случае Е > U0 общее решение для волновой функции в области 2 имеет вид
 , (6)
, (6)
где
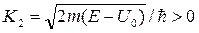 . (7)
. (7)
Учитывая однородность среды в области 2 (по постановке задачи здесь других источников рассеяния нет), амплитуду В2 «встречной» волны в области 2 следует положить равной нулю. При этом А2 является амплитудой волны, прошедшей за ступеньку (частицы, пролетающие над барьером). Таким образом, для Е > U0
 . (8)
. (8)
Физический интерес представляют коэффициенты прохождения и отражения, определяемые отношением плотностей потоков прошедших и отраженных частиц к плотности потока падающих частиц. Для расчета коэффициентов прохождения D и отражения R воспользуемся понятием вектора плотности потока вероятности  (квантовым аналогом классического вектора плотности потока частиц). Выражение для
(квантовым аналогом классического вектора плотности потока частиц). Выражение для  в одномерном случае принимает вид:
в одномерном случае принимает вид:
 . (9)
. (9)
С учетом (9) коэффициент прохождения (коэффициент прозрачности)
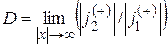 , (10)
, (10)
а коэффициент отражения
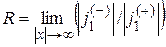 . (11)
. (11)
Вычислим величину вектора плотности потока вероятности в области 2, для этого подставим (8) в (9):
 . (12)
. (12)
Аналогично в области 1 плотность потока вероятности падающих частиц может быть представлена в виде
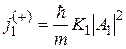 , (13)
, (13)
а плотность потока частиц, отраженных от потенциальной ступеньки,
 . (14)
. (14)
С учетом (10) и (11) имеем
 (15)
(15)
и
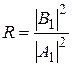 . (16)
. (16)
Таким образом, для определения коэффициентов прохождения и отражения необходимо выразить амплитуды прошедшей и отраженной волн А2 и В1 через амплитуду падающей волны А1.
Чтобы найти А2 и В1 воспользуемся условиями непрерывности волновой функции и сохранения потока частиц. Так как в нашем случае граница двух сред соответствует х = 0, из этих двух условий и вида функций Y1(х) и Y2(х) получим
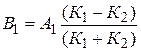 ,
,  , (17)
, (17)
откуда с учетом (1.1.15)-(1.1.17), (1.1.4) и (1.1.7)
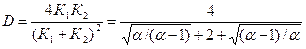 ; (18)
; (18)
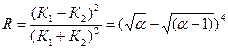 , (19)
, (19)
где a=E/U0.
Плотность потока вероятности частиц при х > 0 равна
 . (20)
. (20)
Полученные результаты сильно отличаются от классических. Согласно законам классической механики частица, обладающая энергией Е > U0, всегда проникает в область 2 (при полной потере кинетической энергии в случае Е = U0).
Согласно законам квантовой механики при Е > U0 имеется конечная вероятность отражения частицы от потенциального барьера, так что в области 1 есть встречный поток отраженных частиц 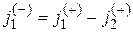 , причем отражение будет полным, если Е = U0. В любом случае D + R = 1.
, причем отражение будет полным, если Е = U0. В любом случае D + R = 1.
Отметим, что для частиц, движущихся к барьеру из +¥, D и R могут быть вычислены тоже по формулам (18) и (19). При заданной полной энергии Е (Е > U0) коэффициенты прохождения и отражения не зависят от направления движения частиц. То есть частицы, движущиеся к барьеру слева, имеют такую же вероятность отразиться от него, что и частицы с той же энергией, движущиеся к барьеру справа. При этом вероятности прохождения и отражения определяются только отношениемЕ/U0. Смена направления движения приводит к изменению фазы отраженной волны. В нашем случае для частиц, падающих на ступеньку слева, отражение происходит в фазе с падающей волной, а при движении справа - в противофазе.
В случае, когда энергия падающей частицы Е < U0, характер решения уравнения (5) радикально меняется. В соответствии с (7) К2 становится мнимым и общее решение (6) будет не комбинация двух волн, распространяющихся в противоположных направлениях, а совокупность двух монотонных функций.
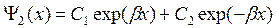 , (21)
, (21)
где  .
.
Учитывая требование конечности волновой функции, необходимо положить С1 = 0 (х > 0). Таким образом, при Е < U0
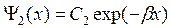 (22)
(22)
«Сшивая» волновые функции (3) и (22) и их производные при х = 0, получим:
 (23)
(23)
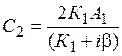 (24)
(24)
Отметим, что в случае Е < U0 амплитуды В1 и С2 - комплекcные числа, а коэффициент отражения R равен единице:
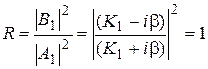
Таким образом, приЕ < U0 все частицы отражаются от потенциальной ступеньки так, что в области 2 поток частиц отсутствует.Несмотря на это, в области 2 волновая функция отлична от нуля, т.е. имеется определенная, хотя и малая, вероятность проникновения частицы внутрь потенциального барьера. В области х > 0
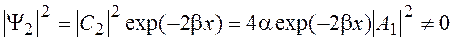
Частица как бы проходит внутрь потенциального барьера и возвращается назад (поток частиц в области 2 отсутствует). При этом между падающей и отраженной волнами появляется фазовый сдвиг:
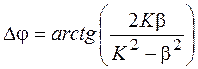
– Конец работы –
Эта тема принадлежит разделу:
ЛЕКЦИЯ №1 ФУНДАМЕНТАЛЬНЫЕ ЯВЛЕНИЯ. ПОЛУПРОВОДНИКОВЫЕ СТРУКТУРЫ И ИХ КЛАССИФИКАЦИЯ
ФУНДАМЕНТАЛЬНЫЕ ЯВЛЕНИЯ ПОЛУПРОВОДНИКОВЫЕ СТРУКТУРЫ И ИХ КЛАССИФИКАЦИЯ... План лекции... Фундаментальные явления...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Рассеяние частиц на потенциальной ступеньке.
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов