рефераты конспекты курсовые дипломные лекции шпоры
Реферат Курсовая Конспект
Частица в прямоугольной потенциальной яме.
Частица в прямоугольной потенциальной яме. - Лекция, раздел Философия, ЛЕКЦИЯ №1 ФУНДАМЕНТАЛЬНЫЕ ЯВЛЕНИЯ. ПОЛУПРОВОДНИКОВЫЕ СТРУКТУРЫ И ИХ КЛАССИФИКАЦИЯ При Выращивании Пленки Узкозонного Полупроводника Между Двумя Слоями Широкозо...
При выращивании пленки узкозонного полупроводника между двумя слоями широкозонного материала может быть реализован потенциальный рельеф, показанный на рис. 1.4.

|
| Рис. 4. Энергетическая диаграмма прямоугольной потенциальной ямы |
В этом случае задача определения стационарных состояний движения электрона сводится к задаче о поведении частицы в прямоугольной потенциальной яме.
Для асимметричной потенциальной ямы (рис. 1.4, а) с
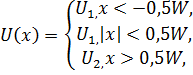
при E< U2 общие решения уравнения (1.1.2) в областях 1 - 3 (с постоянными значениями потенциала) можно представить в виде
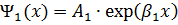
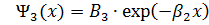
(1.4.1)
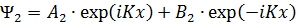
где 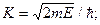
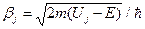
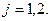
Решения 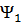 и
и  записаны с учетом того, что они должны равняться нулю на бесконечности.
записаны с учетом того, что они должны равняться нулю на бесконечности.
«Сшивая» волновые функции и их первые производные при x = ±0,5W, придем к уравнению
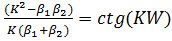 (1.4.2)
(1.4.2)
определяющему значения волнового вектора K, удовлетворяющие условиям данной задачи.
Подставляя  и
и  в (1.4.2), получим трансцендентное уравнение, позволяющее оценить разрешенные значения K:
в (1.4.2), получим трансцендентное уравнение, позволяющее оценить разрешенные значения K:
KW=n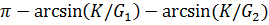 (1.4.3)
(1.4.3)
где п = 1, 2, 3... нумерует разрешенные значения K в порядке их возрастания; 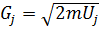 /
/ , j = 1, 2; значения арксинуса надо брать в интервале 0. . .
, j = 1, 2; значения арксинуса надо брать в интервале 0. . .  /2 .
/2 .
Уравнение (1.4.3) определяет набор положительных значений волнового вектора Кп и, следовательно, возможные уровни энергии, соответствующие этим состояниям. Таким образом, энергия  частицы в потенциальной яме оказывается квантованной и принимает одно из разрешенных дискретных значений Еп. Чтобы подчеркнуть это, потенциальные ямы (особенно узкие) часто называют квантовыми ямами (КЯ).
частицы в потенциальной яме оказывается квантованной и принимает одно из разрешенных дискретных значений Еп. Чтобы подчеркнуть это, потенциальные ямы (особенно узкие) часто называют квантовыми ямами (КЯ).
Поскольку аргумент арксинуса не может превышать 1, значения K лежат только в интервале
 . (1.4.4)
. (1.4.4)
Если WG2< , то в КЯ находится не более одного разрешенного энергетического уровня. В общем случае количество разрешенных энергетических уровней в прямoугольной квантовой яме можно оценить, используя неравенство
, то в КЯ находится не более одного разрешенного энергетического уровня. В общем случае количество разрешенных энергетических уровней в прямoугольной квантовой яме можно оценить, используя неравенство
n < (1.4.5)
(1.4.5)
Согласно (1.4.5) при U2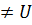 1 всегда найдутся столь малые значения WG2 , для которых в КЯ не будет ни одного разрешенного уровня энергии. Заметим, что при U2 = U1 (рис. 1 .4, б) условие (1.4.5) для п = 1 всегда выполняется. Следовательно, симметричная одномерная потенциальная яма с произвольными значениями W и U всегда имеет не менее одного разрешенного энергетического уровня. Более того, если в случае произвольного одномерного потенциала асимптотические значения
1 всегда найдутся столь малые значения WG2 , для которых в КЯ не будет ни одного разрешенного уровня энергии. Заметим, что при U2 = U1 (рис. 1 .4, б) условие (1.4.5) для п = 1 всегда выполняется. Следовательно, симметричная одномерная потенциальная яма с произвольными значениями W и U всегда имеет не менее одного разрешенного энергетического уровня. Более того, если в случае произвольного одномерного потенциала асимптотические значения  и между ними находится один минимум, то всегда имеется, по крайней мере, один связанный уровень. Если же
и между ними находится один минимум, то всегда имеется, по крайней мере, один связанный уровень. Если же 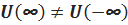 то связанного состояния может и не быть.В случае двух и трех измерений в неглубоких узких потенциальных ямах связанных состояний может не быть даже при
то связанного состояния может и не быть.В случае двух и трех измерений в неглубоких узких потенциальных ямах связанных состояний может не быть даже при  т.е. частица не будет «захватываться» ямой.
т.е. частица не будет «захватываться» ямой.
Отметим, что согласно законам классической механики частица может «захватываться» и совершать финитное движение в любой потенциальной яме, лишь бы энергия частицы была достаточно мала.
Особенно простой вид имеют решения уравнения (1.4.3) для бесконечно больших значений U1 и U2. В случае прямоугольной ямы с бесконечно высокими стенками (БПЯ) согласно (1.4.3)
Kn=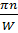 , (1.4.6)
, (1.4.6)
где п = 1, 2, 3... В этом случае на ширине ямы укладывается целое число длин полуволн де Бройля
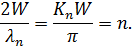
При этом разрешенные дискретные уровни энергии частицы определяются соотношением, эВ:
 (1.4.7)
(1.4.7)
где m0 - масса свободного электрона, W- в нм.
В случае БПЯ нормированные волновые функции частицы в состояниях с различными значениями Еп могут быть представлены в виде
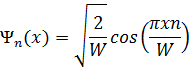
если п - нечетное,
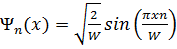 (1.4.8)
(1.4.8)
если п — четное.
Согласно (1.4.8) волновая функция основного состояния 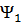 (состояния с наименьшей энергией) не имеет нулей внутри квантовой ямы, функция
(состояния с наименьшей энергией) не имеет нулей внутри квантовой ямы, функция 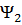 (волновая функция первого возбужденного состояния) имеет один нуль (узел) внутри КЯ, функция
(волновая функция первого возбужденного состояния) имеет один нуль (узел) внутри КЯ, функция  имеет два узла и т.д. Аналогичную зависимость числа узлов волновой функции от номера возбужденного состояния демонстрируют и другие одномерные системы, в которых движение происходит в ограниченной области пространства.
имеет два узла и т.д. Аналогичную зависимость числа узлов волновой функции от номера возбужденного состояния демонстрируют и другие одномерные системы, в которых движение происходит в ограниченной области пространства.
В общем случае, когда  разрешенные значения волнового вектора (а следовательно, и энергии) можно найти, решая уравнение (1.4.3) численно или графически. Однако и в этом случае удается получить ряд соотношений, облегчающих практические оценки.
разрешенные значения волнового вектора (а следовательно, и энергии) можно найти, решая уравнение (1.4.3) численно или графически. Однако и в этом случае удается получить ряд соотношений, облегчающих практические оценки.
Во-первых, можно показать, что

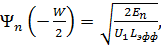 (1.4.9)
(1.4.9)
здесь 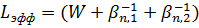 представляет собой эффективную длину области локализации частицы с энергией Еп и отражает тот факт, что частица, преимущественно локализованная внутри КЯ, все же проникает и в области барьеров.
представляет собой эффективную длину области локализации частицы с энергией Еп и отражает тот факт, что частица, преимущественно локализованная внутри КЯ, все же проникает и в области барьеров.
Во-вторых, раскладывая arcsin в ряд, можно получить выражение для оценки разрешенных значений волнового вектора. Полагая Еп<<Uj, получим
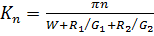 (1.4.10)
(1.4.10)
В первом приближении R1 =R2=1, При этом для Еп/Uтiп <0,25 ошибка в оценке Кп по (1.4.10) будет менее 5 %, Во втором приближении следует полагать
 (1.4.11)
(1.4.11)
здесь 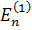 - энергия n-го уровня, рассчитанная в первом приближении при Rj=1. При использовании Rj в виде (1.4.11) ошибка в оценке Кп по (1.4.10) будет менее 2 % для Еп/Umin < 0,3 .
- энергия n-го уровня, рассчитанная в первом приближении при Rj=1. При использовании Rj в виде (1.4.11) ошибка в оценке Кп по (1.4.10) будет менее 2 % для Еп/Umin < 0,3 .
В-третьих, для симметричной КЯ (рис. 1.4, б) волновая функция, соответствующая состояниям положительной четности (n = 1 3,5...), может быть представлена в виде
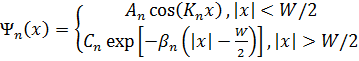 (1.4.12)
(1.4.12)
где
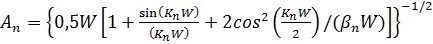 (1.4.13)
(1.4.13)
Волновая функция, соответствующая состояниям отрицательной четности (n= 2, 4, 6...),
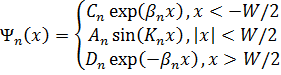 (1.4.14)
(1.4.14)
здесь

Cn=-Dn (1.4.15)
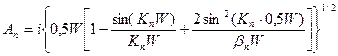
Для симметричной КЯ ширины W и глубины U0, введя нормированные переменные Y = Е/Е* и Х = U0/Е* (Е*= - энергия первого разрешенного уровня в БПЯ), выражение (1.4.2) можно представить в виде
- энергия первого разрешенного уровня в БПЯ), выражение (1.4.2) можно представить в виде
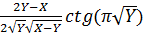 (1.4.16)
(1.4.16)
Анализ (1.4.16) показывает, что в симметричной КЯ конечной глубины для 0<Х≤1 возможно существование лишь одного разрешенного состояния с энергией Е1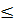 Е*, для 1<x
Е*, для 1<x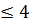 количество разрешенных состояний равно 2, для 4<X
количество разрешенных состояний равно 2, для 4<X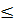 9 равно 3 и т.д. Кроме того, если в симметричной квантовой яме возможно существование n-го энергетического состояния (с n
9 равно 3 и т.д. Кроме того, если в симметричной квантовой яме возможно существование n-го энергетического состояния (с n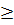 2), то
2), то  независимо от глубины КЯ U0 а общее число разрешенных энергетических уровней п в симметричной прямоугольной КЯ можно оценить, используя неравенство
независимо от глубины КЯ U0 а общее число разрешенных энергетических уровней п в симметричной прямоугольной КЯ можно оценить, используя неравенство
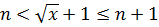
Выполнив разложение (1.4.3) при Y/X<<1 (большие значения W и (или) U0), для основного состояния в первом приближении получим, что
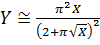 (1.4.17a)
(1.4.17a)
Возникающая при такой аппроксимации ошибка представлена на рис. 1.5. Видно, что при Y>0,37 ошибка определения положения первого разрешенного энергетического уровня в КЯ не превысит 5 %.

|
| Рис.1.5. Характер ошибки, возникающей при аппроксимации выражения (1.4.16): Кривая 1- с использованием (1.4.17а), 2 - с использованием (1.4.17б), 3 - с использованием (1.4.17в), 4 - с использованием (1.4.19), 5 - с использованием (1.4.20) |
Во втором приближении выражение для оценки Y принимает вид
 (1.4.17б)
(1.4.17б)
Такая аппроксимация дает ошибку меньше 5 % для Y ≥ 0,13. Если в (1.4.17б) изменить коэффициент перед 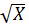 в круглых скобках, т.е. положить, что
в круглых скобках, т.е. положить, что
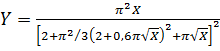 (1.4.17в)
(1.4.17в)
то погрешность определения Y станет меньше 5 % уже для Y ≥ 0,04
При очень малых W (узкая КЯ) разложение (1.4.3) в ряд для симметричной КЯ позволяет представить выражение для оценки энергии основного состояния в виде
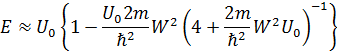
или в переменных X и Y
Y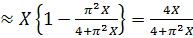 (1.4.186)
(1.4.186)
Данное выражение можно использовать только при очень малых W. Анализ показывает, что расширить интервал приемлемых оценок положения основного состояния в КЯ в области малых X можно, изменяя коэффициент перед X в знаменателе (1.4.18б). На рис. 1.5 представлено поведение ошибки 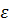 при использовании выражения
при использовании выражения
Y (1.4.19)
(1.4.19)
Еще лучшие результаты могут быть достигнуты при использовании выражения
 (1.4.20)
(1.4.20)
Существует и другая возможность для оценки энергетического положения разрешенных состояний в симметричной КЯ конечной глубины. В этом случае, используя (1.4.16), рассчитывают зависимости Х от Y. При этом
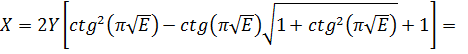
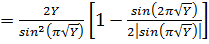 . (1.4.21)
. (1.4.21)
Зависимости Х(Y) для первых трех энергетических уровней, рассчитанные с использованием (1.4.21), приведены на рис. 1.6. По ним, задаваясь параметрами КЯ W, U0 и т (т.е. X), можно определить Y и энергетическое положение уровней. Видно, что для КЯ заданной ширины с уменьшением глубины U0 (т.е. X) будут происходить уменьшение энергии разрешенных состояний Y и последовательное выталкивание их из ямы (т.е. уровни будут сгущаться медленнее, чем уменьшается глубина ямы). Причем при изменении U0 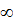 до En-1(
до En-1(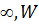 ) энергия n-го уровня в КЯ конечной глубины будет уменьшаться от Еп(
) энергия n-го уровня в КЯ конечной глубины будет уменьшаться от Еп(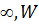 ) лишь до En-1(
) лишь до En-1(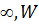 ), а при дальнейшем уменьшении U0 п-й уровень будет вытолкнут из ямы.
), а при дальнейшем уменьшении U0 п-й уровень будет вытолкнут из ямы.
Решив одномерную задачу, в данном случае легко получить решение и для двумерного, и для трехмерного случая. Например, если частица движется в потенциальном поле U=U(x)+U(y)+U(z), где
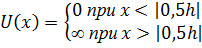 ,
, 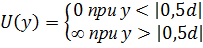 ,
,
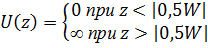 ,
,
то ее волновая функция 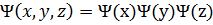 , a E=E1+E2+E3. В этом случае трехмерное уравнение Шредингера распадается на три независимых одномерных уравнения:
, a E=E1+E2+E3. В этом случае трехмерное уравнение Шредингера распадается на три независимых одномерных уравнения:
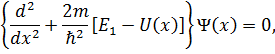
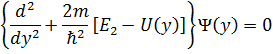
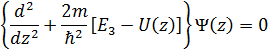

|
| Рис.1.6. Зависимость X(Y) для первых трёх энергетических уровней с n=1,2 и 3 (кривые 1-3 соответственно), рассчитанные с использованием выражения (1.4.21) |
Таким образом, чтобы получить решение для данной трехмерной задачи, достаточно решить одно из этих уравнений (что мы уже сделали ранее) и по аналогии записать решения для двух других уравнений. Отметим, что при h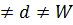 каждому значению энергии будет соответствовать одна волновая функция
каждому значению энергии будет соответствовать одна волновая функция 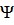 (х,у,z). Другими словами, в системе отсутствуют вырожденные состояния. В случае h=d=W симметрия поля совпадет с симметрией куба и система может иметь двукратно и трехкратно вырожденные уровни. Кроме того, особый характер зависимости потенциальной энергии от координаты в данном случае может приводить к дополнительному (случайному) вырождению.
(х,у,z). Другими словами, в системе отсутствуют вырожденные состояния. В случае h=d=W симметрия поля совпадет с симметрией куба и система может иметь двукратно и трехкратно вырожденные уровни. Кроме того, особый характер зависимости потенциальной энергии от координаты в данном случае может приводить к дополнительному (случайному) вырождению.
– Конец работы –
Эта тема принадлежит разделу:
ЛЕКЦИЯ №1 ФУНДАМЕНТАЛЬНЫЕ ЯВЛЕНИЯ. ПОЛУПРОВОДНИКОВЫЕ СТРУКТУРЫ И ИХ КЛАССИФИКАЦИЯ
ФУНДАМЕНТАЛЬНЫЕ ЯВЛЕНИЯ ПОЛУПРОВОДНИКОВЫЕ СТРУКТУРЫ И ИХ КЛАССИФИКАЦИЯ... План лекции... Фундаментальные явления...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Частица в прямоугольной потенциальной яме.
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов