рефераты конспекты курсовые дипломные лекции шпоры

Раздел Философия
/
Вид работы: Лекции
/
Интерференционные эффекты при надбарьерном пролете частиц.

Реферат Курсовая Конспект

Выберите учебное заведение

Интерференционные эффекты при надбарьерном пролете частиц.

Интерференционные эффекты при надбарьерном пролете частиц. - Лекция, раздел Философия, ЛЕКЦИЯ №1 ФУНДАМЕНТАЛЬНЫЕ ЯВЛЕНИЯ. ПОЛУПРОВОДНИКОВЫЕ СТРУКТУРЫ И ИХ КЛАССИФИКАЦИЯ Рассмотрим Особенности Прохождения Частицы Над Прямоугольным Потенциальным Б...

Рассмотрим особенности прохождения частицы над прямоугольным потенциальным барьером (рис. 1.2, а), когда E>U₁, и E>U₂. Сразу отметим, что надбарьерное прохождение частиц может служить одним из простейших примеров проявления квантовых размерных эффектов. Последние в этом случае приводят к квазипериодической осцилляции коэффициента прохождения частиц при изменении их энергии Е.

В данном случае решение уравнения Шредингера для всех трех областей будет иметь вид

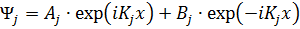здесь j- номер области. При этом, в отличие от (1.2.1),

К₂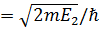 (1.3.1)

где Е₂ =E-U₁.

Полагая, как и ранее, что частицы движутся слева направо, в отсутствии рассеяния можно получить

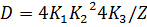, (1.3.2)

R = 1-D; (1.3.3)

Заметим, что выражения (1.3.2), (1.3.3) переходят в (1.2.5), (1.2.6), если учесть, что К₂ =-i

В случае симметричного барьера, когда К₁ = К₃ (рис. 1.2, б), выражения (1.3.2) и (1.3.3) упрощаются и принимают вид

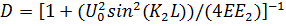(1.3.4)

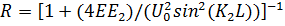(1.3.5)

Анализ (1 .3.4) и (1.3.5) показывает, что при изменении энергии частицы Е будут наблюдаться осцилляции коэффициентов прохождения и отражения. При этом, когда D=D_max, то R = R_min , и наоборот. Период осцилляции соответствует условию

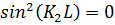
или

K_2,_nL=n (1.3.6)

при выполнении, которого коэффициент прохождения для частиц с волновым вектором K_2,_n обращается в единицу. В этом случае для частиц с энергией

Е_2,_n=Е-U₀ (1.3.7)

на ширине барьера L укладывается целое число полуволн де Бройля и коэффициент отражения равен нулю. Квазиклассически это можно трактовать как результат интерференции волн, отраженных от скачков потенциала на границах барьера. Условие (1.3.7) можно еще записать в виде

(1.3.8)

Величина V_n равна энергии n-го уровня частицы, локализованной внутри потенциальной ямы шириной L с бесконечно высокими стенками, т.е. резонансные значения энергии Е_2,_n совпадают с энергией n-го уровня такой ямы.

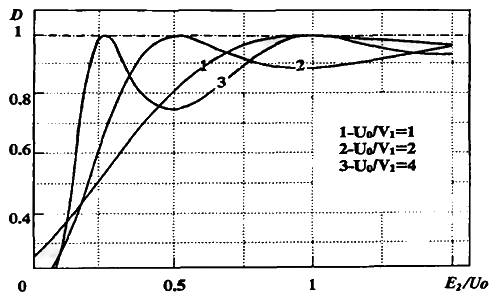
При изменении энергии частицы коэффициент прохождения осциллирует, как показано на рис. 1.3. Минимальные значения D=D_min, соответствующие им значения Е'_2п («антирезонансные» состояния) можно приближенно оценить из условия

Отсюда

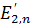остаются постоянными (рис. 1.3).

Используя предыдущие рассуждения (симметричный барьер), можно получить выражение для оценки отношения концентрации

Рис. 1.3 Зависимости коэффициента прохождения над потенциальным барьером от энергии

частиц в окрестности точки с координатой 0 < x < L (над барьером) к концентрации частиц в падающей волне (см. рис. 1.2, б)

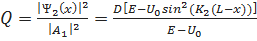(1.3.11)

здесь D определяется выражением (1.3.4).

Согласно (1.3.11) для частиц, имеющих энергию Е, удовлетворяющую условию (1.3.6), когда D> D_m_ах = 1, получим

Q(x=0) =1, Q(x=L/2)=E/(E-U₀)=1+(U₀/E₂), Q(x=L)=1 (1.3.12)

Следовательно, в данном случае концентрация частиц с энергией E в области, занимаемой барьером, будет больше, чем в падающей волне, т.е., несмотря на то, что при Е > U₀ волновая функция электрона «размазана» по всему пространству, существуют избранные значения энергии (и импульса) Е_т при которых вследствие интерференции электронных волн, отраженных от границ барьера, амплитуда волновой функции в области барьера будет больше, чем в других областях.

Сделанные выводы справедливы и в случае несимметричного барьера (см. рис. 1.2, а, в, г). Однако при этом D_m_ах будет меньше единицы, поэтому все эффекты выражены слабее.

В реальных полупроводниковых структурах наблюдать и тем более использовать на практике квантовые осцилляции вероятности надбарьерного прохождения носителей заряда достаточно трудно, поскольку над барьером могут проходить лишь «горячие» электроны, причем увеличение эффекта за счет более высоких барьеров требует соответствующего повышения их энергии. Кроме того, уменьшение коэффициента прохождения при увеличении энергии электронов, которое в принципе могло бы привести к появлению падающего участка на ВАХ структуры, реально оказывается либо малым, либо происходит на интервале энергий 30.. .50 мэВ, сравнимом с тепловым разбросом при комнатной температуре, и поэтому при температурах выше комнатной сильно размыто.

Развернуть

Открыть в широком формате

– Конец работы –

Эта тема принадлежит разделу:

ЛЕКЦИЯ №1 ФУНДАМЕНТАЛЬНЫЕ ЯВЛЕНИЯ. ПОЛУПРОВОДНИКОВЫЕ СТРУКТУРЫ И ИХ КЛАССИФИКАЦИЯ

ФУНДАМЕНТАЛЬНЫЕ ЯВЛЕНИЯ ПОЛУПРОВОДНИКОВЫЕ СТРУКТУРЫ И ИХ КЛАССИФИКАЦИЯ... План лекции... Фундаментальные явления...

Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Интерференционные эффекты при надбарьерном пролете частиц.

Что будем делать с полученным материалом:

Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:

Все темы данного раздела:

Фундаментальные явления.
Поведение подвижных носителей заряда (электронов и дырок) в наноразмерных структурах определяют три группы фундаментальных явлений: квантовое ограничение, баллистический транспорт и квантовая интер

Гетеропереходы первого и второго типов.
Рассмотрим одиночный гетеропереход между двумя полупроводниками A и B, имеющими в общем случае различную ширину запрещенной зоны

Энергетическая диаграмма одномерной сверхрешётки
Полупроводниковые квантово-размерные структуры на основе гетеропереходов принято различать по числу направлений, вдоль которых происходит ограничение движения носителей заряда (электронов или дырок

Рассеяние частиц на потенциальной ступеньке.
Проведем анализ системы, в которой частицы, испускаемые источником, удаленным на большое расстояние, рассеиваются на той или иной преграде, уходя после этого в бесконечность. Простейшей м

Потенциальный барьер конечной ширины.
В реальной физической ситуации мы всегда имеем дело с барьером конечной ширины. Найдем коэффициенты отражения и прохождения при движении частицы через прямоугольный потенциальный барьер ширины

Частица в прямоугольной потенциальной яме.
При выращивании пленки узкозонного полупроводника между двумя слоями широкозонного материала может быть реализован потенциальный рельеф, показанный на рис. 1.4.

Особенности движения частиц над потенциальной ямой.
Мы рассмотрели случай, когда полная энергия частицы Е меньше высоты стенок потенциальной ямы (финитное движение). Здесь размерный эффект проявляется в квантовании энергии и волнового вектора

Движение частицы в сферически симметричной прямоугольной потенциальной яме.
Развитие нанотехнологии инициировало широкое исследование новых классов нанообъектов, в частности квантовых точек, в которых осуществляется пространственное ограничение носителей заряда в трех из

Энергетические состояния в прямоугольной квантовой яме с бесконечными стенками и дополнительным провалом.
Возможность получения слоев с произвольным профилем изменения состава позволила для улучшения характеристик приборов использовать структуры с КЯ сложной формы. Так, для создания нового поколения

Энергетическая диаграмма квантовой ямы с конечными стенками и дополнительным провалом.
В реальности мы имеем дело с потенциальными ямами, стенки которых имеют конечную высоту (см. рис. 1.9, а). Рассмотрим влияние конечной высоты стенок на разрешенные значения энергии основног

Структура со сдвоенной квантовой ямой. Энергетический спектр частицы в системе с δ-образным барьером.
Выше мы рассмотрели поведение частиц в системах, содержащих изолированные КЯ и потенциальные барьеры. Как уже отмечалось, накопленный к настоящему времени опыт и достижения техники для выращивани

Прохождение частицы через многобарьерные квантовые структуры.
При исследовании поведения частицы (электрона) в системах, содержащих изолированные КЯ и потенциальные барьеры, установлено, что при туннелировании через одиночный потенциальный барьер коэффициен

Электрон-фононное рассеяние.
Расчеты механизмов электрон-фононного рассеяния в низкоразмерных полупроводниковых структурах показывают, что они во многом схожи с процессами в объемных полупроводниках, например, такое рассеяни

Межподзонное рассеяние.
Рассмотрим двумерную электронную систему, локализованную в потенциальной яме, входящей в состав модулированно-легированной гетероструктуры или полевого МОП-транзистора. Очевидно, что при достаточн

Экспериментальные данные по продольному переносу
На рис. 6.2 представлены данные, иллюстрирующие прогресс, достигнутый в области повышения подвижности электронов при продольном переносе за последние двенадцать лет в наноструктурах на основе GаАs,

Продольный перенос горячих электронов
В некоторых типах полевых транзисторов и наноструктур кинетическая энергия электронов, ускоряемых электрическим полем, может становиться очень высокой и значительно превышать равновесную тепловую

Поперечный перенос в наноструктурах в электрическом поле.
В этом разделе мы рассмотрим движение носителей в направлении, перпендикулярном плоскостям потенциальных барьеров, разделяющих квантовые гетероструктуры. Такой вид переноса часто ассоциируется с

Резонансное туннелирование
Резонансное туннелирование (РТ) сквозь двойной потенциальный барьер является одним из явлений вертикального квантового переноса, уже нашедший широкое практическое применение в создании диодов и тр

Влияние поперечных электрических полей на свойства сверхрешеток
Ранее уже указывалось, что электронные состояния в сверхрешетках образуют электронные зоны или подзоны, которые гораздо уже, чем соответствующие зоны в обычных кристаллах. Малая ширина зон и энерг

Квантовый перенос в наноструктурах
Рассмотрим далее процессы квантового переноса, происходящие при протекании через наноструктуры тока от присоединенных к ним внешних источников. Такие процессы можно также назвать мезоскопическим

Квантовая проводимость. Формула Ландауэра.
Для самого простого описания эффектов квантовой проводимости удобно рассмотреть одномерную мезоскопическую полупроводниковую структуру, типа квантовой проволоки. Если такая проволока является дос

Формула Ландауэра — Бюттикера для квантового переноса в многозондовых структурах
Полученное в предыдущем разделе выражение (6.15), описывающее квантовый перенос в наноструктуре с двумя контактами, может быть обобщено на случай систем с большим числом контактов. Рассмотрим, на