Теорема Лагранжа об устойчивости положения равновесия

Пусть консервативная механическая система имеет положение равновесия, т.е. положение, в котором она остается бесконечно долго, если она имела в этом положении нулевые обобщенные скорости. Пусть значения обобщенных координат в положении равновесия равны нулю. Пусть также значение потенциальной энергии в этом положении равно нулю:

.

Положение равновесия называется устойчивым, если 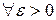такое, что из условий следует

при, .

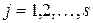Теорема: если в некотором положении равновесия консервативной системы потенциальная энергия имеет строгий минимум, то это положение равновесия является устойчивым.

Доказательство теоремы предполагает «конструирование» величины по заданной величине . Идея доказательства для случая одной переменной изображена на рис. 17.

Если помимо потенциальных и гироскопических сил действуют еще и диссипативные силы, имеющие строго отрицательную мощность, то изолированное положение равновесия является асимптотически устойчивым: 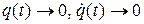при .

Предложение. Определение устойчивого положения равновесия сформулировано для безразмерных обобщенных координат и безразмерного времени. Рассмотрите случай размерных величин. Введите масштабные коэффициенты и попробуйте сформулировать вновь это определение.

Рис. 17. Потенциальная энергия системы с одной степенью свободы

 

4.4.2. Малые колебания консервативной системы вблизи положения устойчивого равновесия

Пусть в положении устойчивого равновесия 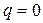, т.е. и пусть .

Рассмотрим движение консервативной системы вблизи положения равновесия. Разложим функцию в окрестности точки равновесия в ряд Маклорена:

По условию 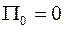; кроме того, согласно принципу виртуальных перемещений в положении равновесия обобщенные силы

.

Отбрасывая члены третьего и высших порядков малости относительно и обозначая 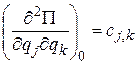, получим

.

 

Пусть связи стационарны. Разложим в выражении 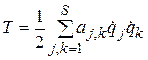коэффициенты также в ряды:

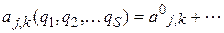
С точностью до малых второго порядка включительно имеем:

.

Таким образом, кинетическая энергия и потенциальная энергия представлены как соответствующие положительно определенные квадратичные формы обобщенных скоростей и координат. Уравнения Лагранжа-2 приобретают вид следующей линейной системы:

.

Будем искать решение этой системы в следующем виде:

.

Подставив в систему дифференциальных уравнений эти формулы и приравняв коэффициенты при , получим систему однородных линейных уравнений относительно амплитуд :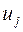

, .

Нетривиальное решение последняя система имеет при условии равенства нулю ее определителя, т.е.

.

Данное уравнение называется частотным уравнением, или вековым. Оно является уравнением 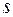- той степени относительно . Благодаря симметричности и положительной определенности матрицы квазиинерционных коэффициентов и симметричности матрицы квазиупругих коэффициентов все корни векового уравнения являются неотрицательными. Каждому корню соответствует своя система однородных линейных уравнений относительно амплитуд . Так как определитель системы равен нулю, существует бесконечно много ее решений. Если положить, например,

, то остальные амплитуды 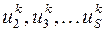выражаются из системы уже однозначно и представляют собой отношения соответствующих амплитуд к первой амплитуде. Совокупность этих отношений называется формой колебаний, соответствующей частоте 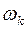. Отношения амплитуд называют также коэффициентами форм.

Квадратичные формы и можно одним и тем же неособенным преобразованием переменных («неособенное» означает) привести обе к диагональному виду, и тогда дифференциальные уравнения движения будут иметь вид

, .

Новые обобщенные координаты называются нормальными координатами колебательной системы.

 

Список литературы

 

1. Яблонский А. А.Курс теоретической механики: учебник длястудентов высших учебных заведений, обучающихся по техническим специальностям. - 15-е изд., стер. - Москва: КноРус, 2010 . - 603 с.

2.Тарг С. М.Краткий курс теоретической механики: учебникдля студентов высших технических учебныхзаведений. - Изд. 20-е, стер. - Москва : Высшая школа, 2010. - 415 с.

3. Бутенин Н.В., Лунц Я.Л., Меркин Д.Р. и др. Курс теоретической механики : учебное пособие для студентов вузов, обучающихся по техническим специальностям : в 2 т. / - Изд. 10-е, стер. – Санкт-Петербург: Лань, 2008. - 729 с. : ил. Т. 1: Статика и кинематика; Т. 2: Динамика.

4. Гантмахер Ф. Р. Лекции по аналитической механике : [учеб. пособие для вузов]. - Изд. 3-е, стер. - М. : Физматлит, 2005. - 262 с.

5. Лойцянский Л.Г., Лурье А.И.Курс теоретической механики : учебное пособие для студентов высших учебных заведений, обучающихся по специальностям 010500 "Механика" : [в 2 т.]. - Изд. 9-е, испр. и доп. - Москва : Дрофа, 2006. - Т. 1: Статика и кинематика. - 2006. - 447 с. : ил. Т. 2: Динамика. - 2006. - 719 с.

6. Поляхов Н.Н., Зегжда С.А., Юшков М.П.; Под ред. проф. Товстика П.Е. Теоретическая механика : Учеб. для студентов вузов, обучающихся по направлениям и специальностям "Математика" и "Механика" [Федер. целевая программа книгопечатания России]. - 2-е изд., перераб. и доп. - М. : Высш. шк., 2000. - 591, [1] c. : ил.

7. Никитин Н.Н. Курс теоретической механики: Учеб. для студентов машиностроит. и приборостроит. специальностей вузов. - 6-е изд., перераб. и доп. - М. : Высш. шк., 2003. - 718, [1] с.: ил.

8. Бать М. И., Джанелидзе Г. Ю., Кельзон А.С. Теоретическая механика в примерах и задачах, ч.1, 2, 3. —М.: Физматгиз, 1995.

 

Quantus tremor est futurus.

Judex ergo cum sedebit.

Quando judex est venturus,

Quidquid latet, apparebit.

Cuncta stricte discussurus.

Nil inultum remanebit!

 

(“Dies irae”)