рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Философия
- /
- Теорема об изменении кинетической энергии
Реферат Курсовая Конспект
Теорема об изменении кинетической энергии
Теорема об изменении кинетической энергии - раздел Философия, ТЕОРЕТИЧЕСКАЯ МЕХАНИКА Опорный конспект лекций Эта Теорема Динамики Применяется В Задачах Механики В Следующих Ситуациях:...
Эта теорема динамики применяется в задачах механики в следующих ситуациях:
- когда условие задачи сформулировано в терминах сила – скорость – перемещение;
- когда требуется исключить реакции идеальных связей (не совершающие работы);
- когда в задаче используются постулаты иных разделов физики (понятие энергии существует не только в механике).
Силы удобно разбить на два класса: внешние и внутренние.
В дифференциальной форме
 или
или 
( - суммарная мощность внешних и внутренних сил) теорема об изменении кинетической энергии применяется для исследования мгновенного состояния механической системы.
- суммарная мощность внешних и внутренних сил) теорема об изменении кинетической энергии применяется для исследования мгновенного состояния механической системы.
В интегральной форме теорема применяется, когда требуется сравнить состояния системы в начальном и конечном ее положениях:
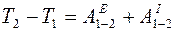 .
.
Здесь 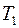 - кинетическая энергия системы в начальном положении,
- кинетическая энергия системы в начальном положении,  - в конечном положении,
- в конечном положении,  и
и  - работа внешних и внутренних сил при перемещении системы из начального положения в конечное положение.
- работа внешних и внутренних сил при перемещении системы из начального положения в конечное положение.
3.2.16. Теорема об изменении количествадвижения. Импульсные функции.
Теорема об изменении количества движения применяется в условиях, когда
- исследуется поступательное движение тел системы;
- требуется исключить внутренние силы;
- в условии задачи фигурирует время движения;
- существенна информация о направлении движения;
- задаются импульсы сил как таковые (без разделения на собственно силу и время).
Дифференциальные формы записи теоремы:
а) 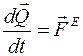 ,
,
б) 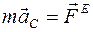 (теорема о движении центра масс),
(теорема о движении центра масс),
в) 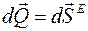 ,
,
где  - суммарный элементарный импульс внешних сил.
- суммарный элементарный импульс внешних сил.
Теорема об изменении кол-ва движения в интегральной форме
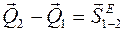 ,
,
где 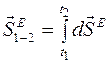 - суммарный импульс внешних сил, приобретенный системой за время перехода из начального состояния 1 в конечное состояние 2.
- суммарный импульс внешних сил, приобретенный системой за время перехода из начального состояния 1 в конечное состояние 2.
Удар тел друг о друга происходит в течение очень малого промежутка времени, и зависимость ударной силы от времени на этом промежутке установить затруднительно. Анализ таких явлений удобно производить с использованием импульсных функций. Определим функцию 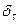 (рис. 11, а):
(рис. 11, а):
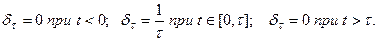
При этом величина интеграла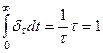 .
.

а б
Рис. 11. Импульсные функции
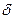 -функцией Дирака (импульсной функцией нулевого порядка) называется функция
-функцией Дирака (импульсной функцией нулевого порядка) называется функция 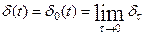 ; при этом
; при этом 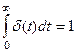 .
.
В теории обобщенных функций 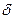 -функция определяется как производная от ступенчатой
-функция определяется как производная от ступенчатой 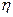 -функции:
-функции: 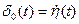 . В свою очередь, производной от импульсной функции нулевого порядка является импульсная функция первого порядка:
. В свою очередь, производной от импульсной функции нулевого порядка является импульсная функция первого порядка: 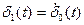 и т.д. Каждая импульсная функция может быть определена отдельно, подобно вышеприведенному определению функции нулевого порядка (рис. 11,б). При исследовании процессов, происходящих во времени,
и т.д. Каждая импульсная функция может быть определена отдельно, подобно вышеприведенному определению функции нулевого порядка (рис. 11,б). При исследовании процессов, происходящих во времени, 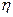 -функция считается безразмерной. Тогда
-функция считается безразмерной. Тогда 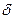 -функция нулевого порядка имеет размерность с-1,
-функция нулевого порядка имеет размерность с-1,  - размерность с-2 и т.д.
- размерность с-2 и т.д.
Пусть гармонический осциллятор при нулевых начальных условиях испытывает внешнее силовое воздействие, выражающееся приложенным в момент времени  импульсом силы
импульсом силы  . Уравнение движения:
. Уравнение движения:  , или
, или  . Построим изображения по Лапласу левой и правой частей уравнения:
. Построим изображения по Лапласу левой и правой частей уравнения:
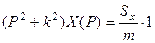 ; отсюда
; отсюда
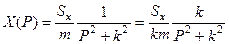 .
.
Переходим к оригиналам: 
(Согласно таблице оригиналов и изображений
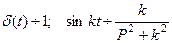 ).
).
Решение соответствует начальному скачку скорости величиной  .
.
3.2.17. Теорема об изменении кинетического момента
используется в условиях, аналогичных п. 3.2.16, но для исследования вращательного движения.
Интегральная форма записи теоремы:
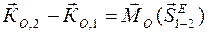 ,
,
где  - суммарный момент импульсов внешних сил относительно полюса О.
- суммарный момент импульсов внешних сил относительно полюса О.
Теорему об изменении кинетического момента (см. п. 2.1.9) можно записать в проекциях на ось 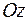 :
:
 ,
,
где 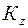 - кинетический момент системы относительно оси
- кинетический момент системы относительно оси 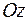 ,
,
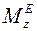 - главный момент внешних сил относительно оси
- главный момент внешних сил относительно оси 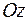 .
.
Применительно к вращающемуся вокруг неподвижной оси  твердому телу получаем уравнение динамики вращающегося твердого тела:
твердому телу получаем уравнение динамики вращающегося твердого тела:
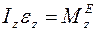 , или
, или 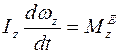 , или
, или  .
.
Каждая из последних двух записей называется дифференциальным уравнением вращательного движения тела.
3.2.18. Физический маятник – твердое тело, которое может вращаться вокруг неподвижной горизонтальной оси, не проходящей через его центр тяжести. Дифференциальное уравнение движения имеет вид
 ,
,
где  - угол отклонения маятника от вертикального его положения – положения устойчивого равновесия,
- угол отклонения маятника от вертикального его положения – положения устойчивого равновесия,  - расстояние от центра тяжести до оси вращения
- расстояние от центра тяжести до оси вращения 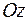 . Это нелинейное дифференциальное уравнение.
. Это нелинейное дифференциальное уравнение.
Рассмотрим малые колебания маятника вблизи положения устойчивого равновесия, считая значения функции  и ее производных малыми величинами одинакового порядка. С точностью до малых второго порядка включительно получаем приближенное дифференциальное уравнение движения
и ее производных малыми величинами одинакового порядка. С точностью до малых второго порядка включительно получаем приближенное дифференциальное уравнение движения
 .
.
Это - линейное уравнение гармонического осциллятора. Отбросив величины высоких порядков малости, мы линеаризовали задачу.
Линеаризованное дифференциальное уравнение малых колебаний математического маятника (см. п. 3.1.19) имеет вид 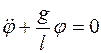 (
(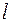 - длина маятника). Сравним уравнения малых колебаний математического и физического маятников. Величина
- длина маятника). Сравним уравнения малых колебаний математического и физического маятников. Величина 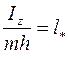 называется приведенной длиной физического маятника.
называется приведенной длиной физического маятника.
Если маятник – однородный стержень длиной 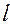 , то
, то 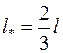 .
.
*3.2.19. Центр удара
Пусть твердое тело вращается вокруг оси  , будучи закреплено в точках А и В (рис. 12). В точке, лежащей на оси
, будучи закреплено в точках А и В (рис. 12). В точке, лежащей на оси  на некотором расстоянии d, прикладывается мгновенная
на некотором расстоянии d, прикладывается мгновенная
сила, импульс которой равен 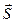 . Рассмотрим вопрос о нахождении вызванных этим ударом ударных реакций опор
. Рассмотрим вопрос о нахождении вызванных этим ударом ударных реакций опор  и
и 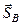 . Теорема об изменении количества движения (п. 3.1.16) дает выражение
. Теорема об изменении количества движения (п. 3.1.16) дает выражение
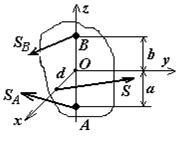
Рис. 12. Центр удара
 .
.
Количество движения тела 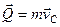 , где
, где 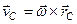 . Записав теорему в проекции на оси, получим:
. Записав теорему в проекции на оси, получим:
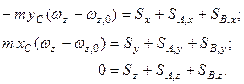
Здесь  означают проекции угловой скорости после и до удара.
означают проекции угловой скорости после и до удара.
Согласно п.3.2.6 кинетический момент вращающегося тела равен
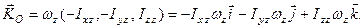
Интегральная форма записи теоремы об изменении кинетического момента в проекциях на оси дает нам уравнения
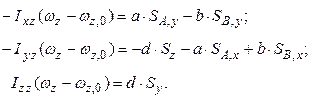
Пусть должны обращаться в нуль ударные реакции 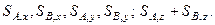 Тогда из шести уравнений движения следует:
Тогда из шести уравнений движения следует:
1) 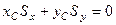 , т.е. удар должен быть направлен перпендикулярно плоскости, проходящей через центр тяжести и ось вращения;
, т.е. удар должен быть направлен перпендикулярно плоскости, проходящей через центр тяжести и ось вращения;
2) 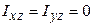 , т.е. ось
, т.е. ось  должна быть главной осью инерции;
должна быть главной осью инерции;
3)  . Это выражение есть приведенная длина физического маятника, при условии, что ось
. Это выражение есть приведенная длина физического маятника, при условии, что ось  проведена через центр тяжести.
проведена через центр тяжести.
*3.2.20. Приближенная теория гироскопа
Гироскопом («указателем вращения») называют твердое тело, имеющее ось симметрии, и совершающее вращение вокруг точки, принадлежащей этой оси. Примем эту ось за ось  собственного вращения. Угловая скорость
собственного вращения. Угловая скорость 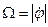 собственного вращения гироскопа весьма велика, так что составляющая
собственного вращения гироскопа весьма велика, так что составляющая  кинетического момента превалирует над другими составляющими. Пусть гироскоп в начале движения имеет угловую скорость
кинетического момента превалирует над другими составляющими. Пусть гироскоп в начале движения имеет угловую скорость  , так что его кинетический момент
, так что его кинетический момент 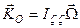 . Приближенная теория гироскопа исследует его движение при малой прецессии и нутации и предполагает, что величина
. Приближенная теория гироскопа исследует его движение при малой прецессии и нутации и предполагает, что величина 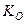 остается практически неизменной. Когда вектор
остается практически неизменной. Когда вектор  поворачивается с угловой скоростью
поворачивается с угловой скоростью 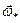 , производная от этого вектора вычисляется по формуле Эйлера-Пуассона
, производная от этого вектора вычисляется по формуле Эйлера-Пуассона 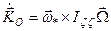 как скорость конца вектора
как скорость конца вектора  (интерпретация Резаля). Согласно теореме об изменении кинетического момента эта скорость равна моменту внешних сил
(интерпретация Резаля). Согласно теореме об изменении кинетического момента эта скорость равна моменту внешних сил 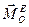 , называемому здесь гироскопическим моментом.
, называемому здесь гироскопическим моментом.
*3.2.21. Удар материальной точки о преграду
Взаимодействие двух твердых тел в результате кратковременного контакта друг с другом называется ударом. Обозначим через  продолжительность удара. Сила взаимодействия
продолжительность удара. Сила взаимодействия  при ударе может достигать большой величины, но при этом ударный импульс
при ударе может достигать большой величины, но при этом ударный импульс  имеет конечную величину. При ударе происходит деформирование соударяющихся тел, сопровождающееся распространением внутри них волн упругих деформаций. Эти волны, отражаясь от свободных поверхностей и интерферируя, создают сложную картину распределения напряжений внутри тел. Величина
имеет конечную величину. При ударе происходит деформирование соударяющихся тел, сопровождающееся распространением внутри них волн упругих деформаций. Эти волны, отражаясь от свободных поверхностей и интерферируя, создают сложную картину распределения напряжений внутри тел. Величина  зависит от этих факторов, как и от скоростей сближения тел. Например, продолжительность соударения двух латунных шаров диаметром 26 мм при относительной скорости сближения 74 мм/с равна
зависит от этих факторов, как и от скоростей сближения тел. Например, продолжительность соударения двух латунных шаров диаметром 26 мм при относительной скорости сближения 74 мм/с равна 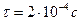 .
.
Пусть тело малых размеров, принимаемое за материальную точку массой  , двигавшееся со скоростью
, двигавшееся со скоростью 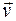 , ударяется о неподвижную преграду (о тело бесконечно большой массы) и отскакивает от преграды со скоростью
, ударяется о неподвижную преграду (о тело бесконечно большой массы) и отскакивает от преграды со скоростью  .
.
Считая, что ударные силы значительно превосходят другие силы, приложенные к материальной точке, пренебрежем импульсами этих других сил. Запишем теорему об изменении количества движения материальной точки:
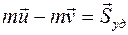 .
.
В простейших задачах об ударе будем пренебрегать и импульсом силы трения, так что проекция скорости точки на касательную плоскость к поверхности преграды не изменяется. Тогда для нормальной составляющей скорости имеем  . Поскольку определение ударного импульса выходит за рамки теоретической механики, введем гипотезу (Ньютона):
. Поскольку определение ударного импульса выходит за рамки теоретической механики, введем гипотезу (Ньютона):
 ,
,
где величина  называется коэффициентом восстановления и считается заранее известной для данного сочетания материалов и форм тел. Этот коэффициент не зависит от скоростей тел и их размеров. Тогда
называется коэффициентом восстановления и считается заранее известной для данного сочетания материалов и форм тел. Этот коэффициент не зависит от скоростей тел и их размеров. Тогда 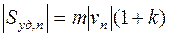 .
.
Коэффициент восстановления принимает значения  . Если
. Если  , то удар называется абсолютно упругим, если
, то удар называется абсолютно упругим, если  , то удар называется абсолютно неупругим.
, то удар называется абсолютно неупругим.
*3.2.22. Прямой удар двух тел
Пусть два тела массами 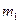 и
и  двигаются вдоль оси
двигаются вдоль оси  и ударяются друг о друга (рис. 14).
и ударяются друг о друга (рис. 14).
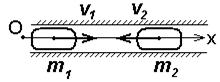
Рис. 14. Прямой удар двух тел
Пусть их скорости до удара равны  и
и  (ось
(ось  направлена в сторону скорости
направлена в сторону скорости  ). Требуется найти их скорости
). Требуется найти их скорости 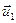 и
и  после удара. Коэффициент восстановления выразим здесь через относительные скорости:
после удара. Коэффициент восстановления выразим здесь через относительные скорости: 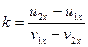 (удар возможен, если тела сближаются, так что знаменатель данной дроби положителен).
(удар возможен, если тела сближаются, так что знаменатель данной дроби положителен).
Применим теорему об изменении количества движения к механической системе, состоящей из соударяющихся тел. Ударные силы здесь внутренние силы, и их импульс равен нулю. Следовательно
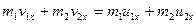 .
.
Используя эту формулу и выражение для коэффициента 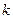 , находим скорости тел после удара:
, находим скорости тел после удара:

При абсолютно неупругом ударе скорости после удара одинаковы.
При абсолютно упругом ударе тела одинаковой массы  обмениваются скоростями:
обмениваются скоростями:
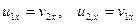 .
.
Обычно рассматривают два этапа удара. Первый этап – от начального соприкосновения соударяющихся тел до их наибольшей деформации, когда относительная их скорость становится равной нулю, и тела приобретают общую скорость (равную скорости центра масс, которая остается неименной в процессе удара). Обозначим величину ударного импульса первого этапа как  . Второй этап – частичное или полное упругое восстановление формы и приобретение телами скоростей
. Второй этап – частичное или полное упругое восстановление формы и приобретение телами скоростей 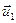 и
и  .
.
Пусть второму этапу соответствует ударный импульс  . Тогда оказывается, что
. Тогда оказывается, что  .
.
Кинетическая энергия системы тел до удара равна  , а после удара
, а после удара 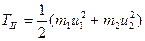 .
.
Выражение 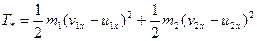 называют кинетической энергией, соответствующей потерянным скоростям
называют кинетической энергией, соответствующей потерянным скоростям  и
и  .
.
Имеет место соотношение  .
.
При абсолютно упругом ударе  , а при абсолютно неупругом
, а при абсолютно неупругом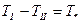 .
.
– Конец работы –
Эта тема принадлежит разделу:
ТЕОРЕТИЧЕСКАЯ МЕХАНИКА Опорный конспект лекций
Федеральное агентство по образованию... Государственное образовательное учреждение высшего профессионального... Санкт Петербургский государственный университет...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Теорема об изменении кинетической энергии
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов