рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Философия
- /
- Геометрия масс. Теоремы динамики
Реферат Курсовая Конспект
Геометрия масс. Теоремы динамики
Геометрия масс. Теоремы динамики - раздел Философия, ТЕОРЕТИЧЕСКАЯ МЕХАНИКА Опорный конспект лекций 3.2.1. Центр Масс (Центр Инерции) Механической Системы...
3.2.1. Центр масс (центр инерции) механической системы
Пусть механическая система состоит из 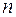 точечных фрагментов. Рассмотрим некоторую точку С пространства и пусть
точечных фрагментов. Рассмотрим некоторую точку С пространства и пусть 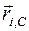 - радиус-вектор
- радиус-вектор  -го фрагмента относительно полюса С (рис. 8). Выражение
-го фрагмента относительно полюса С (рис. 8). Выражение 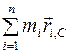 называется статическим моментом масс относительно полюса С. Центр масс системы - такая точка С пространства, относительно которой статический момент равен нулю:
называется статическим моментом масс относительно полюса С. Центр масс системы - такая точка С пространства, относительно которой статический момент равен нулю:
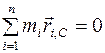 .
.
Пусть  - радиус-вектор
- радиус-вектор  -го фрагмента относительно полюса О абсолютной (инерциальной) системы отсчета,
-го фрагмента относительно полюса О абсолютной (инерциальной) системы отсчета, 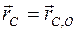 - абсолютный радиус-вектор центра масс;
- абсолютный радиус-вектор центра масс; 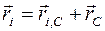 . Тогда, обозначив как
. Тогда, обозначив как  массу системы, получим, что
массу системы, получим, что 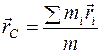 .
.

Рис. 8. Определение положения центра масс
Если тело имеет центр тяжести (центр системы параллельных сил), то он находится в центре масс.
3.2.2. Выражение количества движения системы через скорость центра масс. Уравнение движения центра масс.
Используя определение центра масс, находим, что количество движения системы выражается через скорость 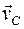 центра масс:
центра масс:
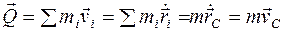 .
.
Теорему об изменении количества движения (Ч. 1, п. 2.1.9) при условии 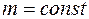 можно представить как уравнение движения центра масс:
можно представить как уравнение движения центра масс:
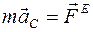 .
.
3.2.3. Теоремы Кёнига
а) Пусть с центром масс связана подвижная система отсчета, движущаяся поступательно, т.е. каждый ее пункт имеет скорость  . Тогда абсолютная кинетическая энергия механической системы равна
. Тогда абсолютная кинетическая энергия механической системы равна
 ,
,
где 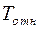 - кинетическая энергия относительного движения системы.
- кинетическая энергия относительного движения системы.
б) Кинетический момент абсолютного движения относительно неподвижного полюса  связан с кинетическим моментом относительно некоторого подвижного полюса
связан с кинетическим моментом относительно некоторого подвижного полюса 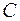 формулой
формулой
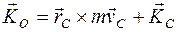 .
.
Если 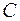 – центр масс, то
– центр масс, то 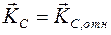 - кинетический момент относительного движения.
- кинетический момент относительного движения.
3.2.4. Кинетическая энергия твердого тела в простейших случаях его движения. Момент инерции тела относительно оси
а) При поступательном движении твердого тела 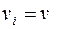 при
при 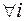
 кинетическая энергия его равна
кинетическая энергия его равна
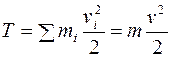 .
.
б) При вращательном движении 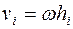 (см. Ч. 1, п. 1.2.8), где
(см. Ч. 1, п. 1.2.8), где 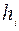 - расстояние от
- расстояние от  -ой точки до оси вращения
-ой точки до оси вращения 
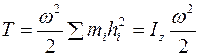 .
.
Выражение 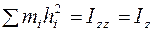 называется моментом инерции тела относительно оси вращения
называется моментом инерции тела относительно оси вращения 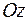 ; оно характеризует разброс масс относительно оси
; оно характеризует разброс масс относительно оси 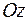 и служит мерой инерционности тела во вращательном движении вокруг этой же оси.
и служит мерой инерционности тела во вращательном движении вокруг этой же оси.
в) При плоскопараллельном движении тела (см. теорему Кёнига)
 .
.
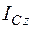 - момент инерции тела относительно оси
- момент инерции тела относительно оси 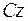 , проходящей через центр масс С перпендикулярно плоскости движения. Если
, проходящей через центр масс С перпендикулярно плоскости движения. Если 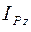 - момент инерции тела относительно оси, проходящей через мгновенный центр скоростей Р, то
- момент инерции тела относительно оси, проходящей через мгновенный центр скоростей Р, то
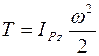 .
.
3.2.5. Кинетический момент вращающегося твердого тела относительно неподвижной оси его вращения
Вектор 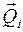 количества движения
количества движения  -ой точки тела направлен так же, как и её скорость
-ой точки тела направлен так же, как и её скорость 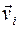 (см. ч. 1, рис. 3). По правилу расчета момента вектора относительно оси (ч. 1, п. 2.1.4) получим, что величина момента вектора
(см. ч. 1, рис. 3). По правилу расчета момента вектора относительно оси (ч. 1, п. 2.1.4) получим, что величина момента вектора 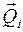 относительно оси вращения
относительно оси вращения 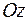 равна
равна 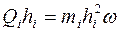 . Знак момента определяется знаком проекции
. Знак момента определяется знаком проекции 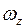 . Кинетический момент всего тела относительно оси
. Кинетический момент всего тела относительно оси 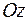
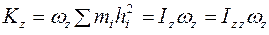 .
.
3.2.6. Кинетический моменти кинетическаяэнергия твердого тела при его сферическом движении. Тензор инерции
При сферическом движении вокруг полюса  скорость
скорость  -ой точки твердого тела равна (см. ч. 1, п. 1.5.4)
-ой точки твердого тела равна (см. ч. 1, п. 1.5.4)
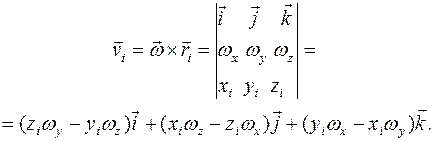
Тогда кинетический момент тела относительно полюса О равен
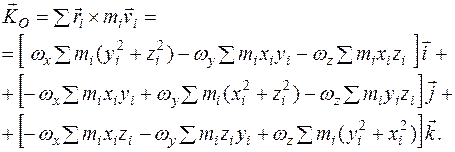
Выражение  есть квадрат расстояния от
есть квадрат расстояния от  -ой точки до оси
-ой точки до оси 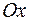 , так что
, так что 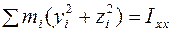 - момент инерции тела относительно оси
- момент инерции тела относительно оси 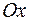 .
.
Выражения 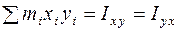 ,
,  ,
, 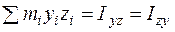 называются центробежными моментами инерции.
называются центробежными моментами инерции.
Симметричная матрица  -
-
матрица инерции - определяет тензор инерции тела в заданной точке.
Тензоры – математические объекты, которые возникли как обобщение понятия о векторах. Скаляр считается тензором нулевого ранга. Вектор в трехмерном пространстве - тензор первого ранга - представляет собой совокупность трех скаляров, перечисляемых в определенной последовательности (кортеж). Тензор второго ранга в трехмерном пространстве можно рассматривать как кортеж из трех векторов.
Пусть прямоугольная декартова система координат 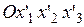 развернута относительно такой же системы
развернута относительно такой же системы 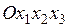 . Обозначим как
. Обозначим как 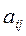 косинусы углов между осями
косинусы углов между осями  и
и 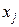 . Между проекциями
. Между проекциями  некоторого вектора
некоторого вектора 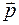 , рассчитанными относительно системы координат
, рассчитанными относительно системы координат 
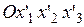 , и проекциями его
, и проекциями его 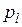 в системе
в системе 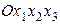 имеют место соотношения:
имеют место соотношения:
 .
.
В такого рода записях символ суммирования опускается; по умолчанию принимается, что суммирование происходит по повторяющимся индексам (в данном случае по индексу 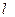 ). Говорят, что векторы
). Говорят, что векторы 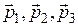 являются компонентами тензора
являются компонентами тензора 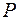 , если эти компоненты преобразуются по аналогичному правилу:
, если эти компоненты преобразуются по аналогичному правилу: 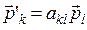 . Таким образом, тензор
. Таким образом, тензор 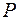 задается девятью скалярами
задается девятью скалярами
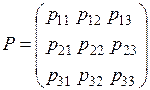 ,
,
которые преобразуются по формуле  .
.
Напряженно-деформированное состояние сплошного упругого тела характеризуется тензором напряжений и тензором деформаций (tendo (лат.) – напрягаю, натягиваю). Обобщенный закон Гука задает соотношения между компонентами этих тензоров через упругие параметры материала тела.
Если 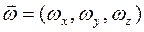 обозначает вектор-строку, а
обозначает вектор-строку, а  - транспонированный вектор (вектор-столбец), то можно записать
- транспонированный вектор (вектор-столбец), то можно записать
 .
.
(Согласно правилу перемножения матриц результат умножения матрицы на столбец есть столбец; результат умножения строки на матрицу - строка.)
Сравним полученное выражение для  с выражением для количества движения при поступательном движении
с выражением для количества движения при поступательном движении 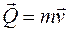 ; их структура одна и та же: произведение инерционного коэффициента на кинематический параметр тела.
; их структура одна и та же: произведение инерционного коэффициента на кинематический параметр тела.
Отметим, что при вращении тела вокруг неподвижной оси 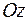
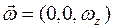 , и тогда
, и тогда
 В выражении для кинетической энергии тела
В выражении для кинетической энергии тела  величины
величины  (
(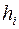 - расстояние от
- расстояние от  -ой точки тела до мгновенной оси вращения
-ой точки тела до мгновенной оси вращения  , вдоль которой направлен вектор
, вдоль которой направлен вектор  ). Тогда
). Тогда
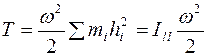 ,
,
где  - момент инерции тела относительно мгновенной оси. С другой стороны, подставив в формулу
- момент инерции тела относительно мгновенной оси. С другой стороны, подставив в формулу 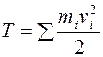 приведенное выше выражение для вектора
приведенное выше выражение для вектора 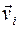 , получим
, получим
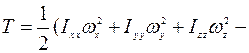
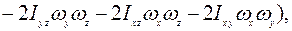
или 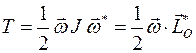 .
.
Сравним: при поступательном движении твердого тела
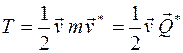 .
.
Рассмотрим орт направления мгновенной оси 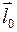 , такой, что
, такой, что 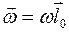 . Тогда
. Тогда 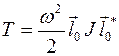 . Из сравнения с вышеприведенной формулой следует, что момент инерции относительно оси
. Из сравнения с вышеприведенной формулой следует, что момент инерции относительно оси  находится по формуле
находится по формуле 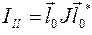 . Пусть ось
. Пусть ось  проходит через точку
проходит через точку  на единичной сфере с центром
на единичной сфере с центром  , имеющую координаты
, имеющую координаты 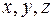 - проекции орта
- проекции орта 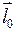 . Тогда получим выражение
. Тогда получим выражение
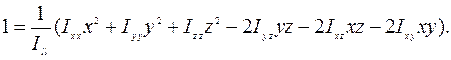 Изменим масштаб расстояний. Если точку М на оси
Изменим масштаб расстояний. Если точку М на оси 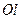 брать на
брать на
расстоянии 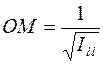 , то получим выражение
, то получим выражение

Это уравнение поверхности второго порядка – эллипсоида инерции. Величины 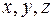 - координаты точки М эллипсоида, при этом расстояние ОМ характеризует момент инерции относительно оси ОМ в соответствии с вышеприведенной формулой. Оси симметрии его называются главными осями инерции. Матрицу
- координаты точки М эллипсоида, при этом расстояние ОМ характеризует момент инерции относительно оси ОМ в соответствии с вышеприведенной формулой. Оси симметрии его называются главными осями инерции. Матрицу 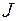 квадратичной формы, определяющей левую часть уравнения эллипсоида, можно с помощью неособенного преобразования, задающего поворот осей координат, привести к диагональному виду. Компоненты диагональной матрицы суть главные моменты инерции. Оси соответствующей системы координат называются главными осями инерции. Центробежные моменты относительно главных осей равны нулю.
квадратичной формы, определяющей левую часть уравнения эллипсоида, можно с помощью неособенного преобразования, задающего поворот осей координат, привести к диагональному виду. Компоненты диагональной матрицы суть главные моменты инерции. Оси соответствующей системы координат называются главными осями инерции. Центробежные моменты относительно главных осей равны нулю.
Можно построить эллипсоид инерции с центром в любой точке тела. Если за центр принять центр масс тела, то оси инерции называются центральными.
3.2.7. Теорема Гюйгенса-Штейнера о соотношении между моментами инерции относительно двух параллельных осей, одна из которых – центральная
Пусть 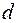 - расстояние между осью
- расстояние между осью  и параллельной ей центральной осью
и параллельной ей центральной осью  ;
;  - масса тела (рис. 9,а). Моменты инерции связаны формулой:
- масса тела (рис. 9,а). Моменты инерции связаны формулой: 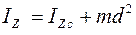 .
.
– Конец работы –
Эта тема принадлежит разделу:
ТЕОРЕТИЧЕСКАЯ МЕХАНИКА Опорный конспект лекций
Федеральное агентство по образованию... Государственное образовательное учреждение высшего профессионального... Санкт Петербургский государственный университет...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Геометрия масс. Теоремы динамики
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов