рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Образование
- /
- ПРОЦЕСС ЮЛА
Реферат Курсовая Конспект
ПРОЦЕСС ЮЛА
ПРОЦЕСС ЮЛА - раздел Образование, АВТОРЕГРЕССИЯ ВТОРОГО ПОРЯДКА ...

Для того чтобы процесс был стационарным, корни 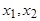 характеристического уравнения
характеристического уравнения 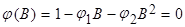 (
(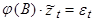 ) должны быть вне единичного круга, т.е.
) должны быть вне единичного круга, т.е. 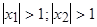 . Это означает, что на параметры авторегрессионого уравнения накладываются следующие ограничения:
. Это означает, что на параметры авторегрессионого уравнения накладываются следующие ограничения:
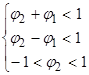
Действительно, если 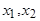 - корни уравнения
- корни уравнения
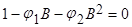 , (1)
, (1)
то уравнение авторегрессии второго порядка
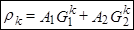 (2)
(2)
можно представить как
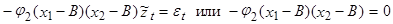 (3)
(3)
Действительно,
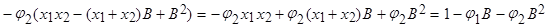
Следовательно,
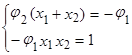 (
(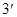 )
)
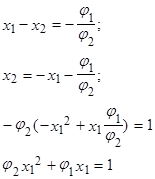
Что и требовалось доказать (пункт 1). Это теорема Виета.
Делаем в уравнении (3) замену переменных:
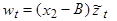 (4)
(4)
тогда 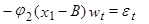 (5)
(5)
(5) можно представить, как 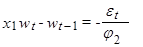
или 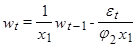 (6)
(6)
Чтобы процесс 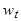 был стационарен,
был стационарен, 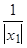 должен быть меньше 1 или
должен быть меньше 1 или 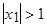 .
.
Аналогично (4) представляем как 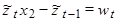
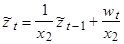 (7)
(7)
Для стационарности процесса 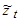 ,
,  должно быть больше 1.
должно быть больше 1.
Действительно, раскрываем (7):

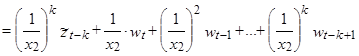
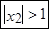 .
.
Аналогично разворачиваем уравнение (6), используя рекурентность составляющих:
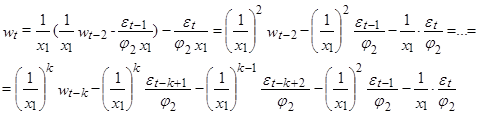
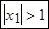 .
.
Для стационарности процессов 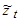 и
и 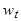 необходимо чтобы
необходимо чтобы 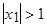 и
и 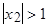 .
.
Какие это накладывает ограничения на 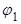 и
и 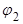 :
:
1. если 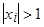 , то
, то 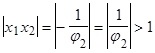 из (
из (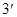 ), отсюда
), отсюда 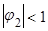 или
или 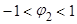
2. уравнение 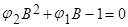 имеет корни:
имеет корни: 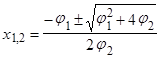 ,
, 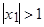 ,
, 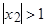 .
.
I. Пусть корни вещественные, т.е. дискриминант 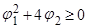 . Возможны следующие ситуации:
. Возможны следующие ситуации:
a) 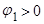 ,
, 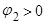 . Выбираем меньший по модулю корень:
. Выбираем меньший по модулю корень:
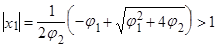
(т.к. модуль положительного числа есть само число, а под корнем значение большее, чем 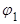 ).
).
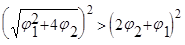
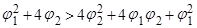 ,
,
т.к. 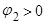 , то делим на
, то делим на 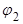 :
:
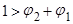 , или
, или 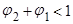
b) 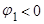 ,
, 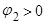 . Второй корень по абсолютной величине меньше, поэтому берем
. Второй корень по абсолютной величине меньше, поэтому берем 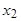 , причем корень больше
, причем корень больше 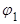 , значит модуль отрицательного числа равен числу, противоположному данному:
, значит модуль отрицательного числа равен числу, противоположному данному:
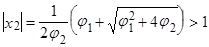
корень - отрицательное число, 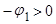 , но меньше по модулю, чем корень.
, но меньше по модулю, чем корень.
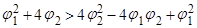 ,
,
т.к. 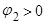 , то:
, то:
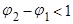
c) 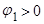 ,
, 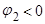 . Меньший по абсолютной величине корень -
. Меньший по абсолютной величине корень - 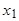 , причем числитель
, причем числитель 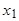 меньше 0:
меньше 0:
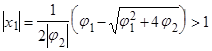
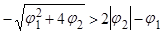 или
или 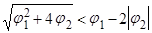
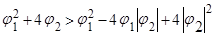
делим на 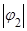 :
:
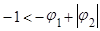 ,
,
т.к. 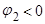 , то модуль
, то модуль 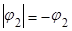 :
:
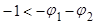 или
или 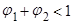
d) 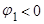 ,
, 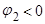 . Меньший по абсолютной величине корень -
. Меньший по абсолютной величине корень - 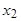 , причем числитель
, причем числитель 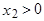 , значит модуль равен самому числу:
, значит модуль равен самому числу:
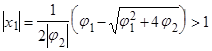
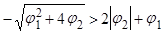
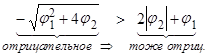
следовательно, при возведении в квадрат знак неравенства меняется на противоположный.
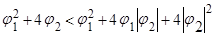
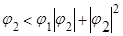
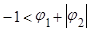
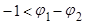 или
или 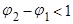
II. Пусть корни 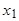 и
и 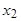 - комплексные, т.е.
- комплексные, т.е. 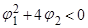 , тогда т.к. квадрат модуля комплексного числа равен сумме квадратов действительной и мнимой частей
, тогда т.к. квадрат модуля комплексного числа равен сумме квадратов действительной и мнимой частей
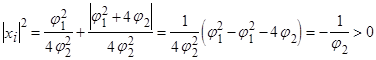 т.к. квадрат числа >0,
т.к. квадрат числа >0,
отсюда 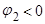 .
.
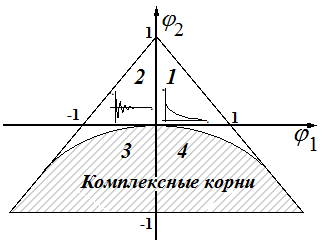
Таким образом, для стационарности процесса 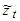 необходимо, чтобы
необходимо, чтобы 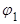 и
и 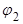 находились в треугольной области:
находились в треугольной области:
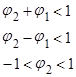 (8)
(8)
Далее посмотрим, как будет выглядеть для (АР2) автокорреляционная функция. Запишем авторегрессионый процесс порядка p:
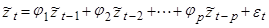
Умножим обе части уравнения на 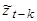 :
:
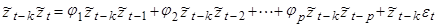
Переходя к математическим ожиданиям получим:
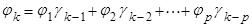 (9)
(9)
Заметим, что матожидание 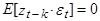 при k > 0, т.к.
при k > 0, т.к. 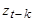 может включать лишь импульсы
может включать лишь импульсы 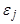 до момента t-k и зависит от
до момента t-k и зависит от 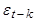 и предшествующих e, но не будущих импульсов.
и предшествующих e, но не будущих импульсов.
Поделив все члены выражения (9) на 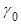 находим выражение для автокорреляционной функции:
находим выражение для автокорреляционной функции:
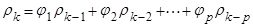 (10)
(10)
Это выражение можно записать иначе, используя оператор сдвига назад:
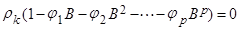 , (11)
, (11)
где 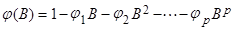 .
.
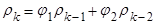
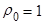
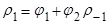
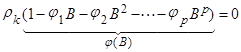
Если 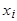 - корни полинома (i = 1, …, p), то по теореме Виета
- корни полинома (i = 1, …, p), то по теореме Виета
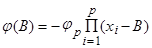
Обозначим через 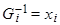 . Т.к. по теореме Виета (из
. Т.к. по теореме Виета (из  )
)
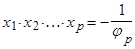 , то
, то
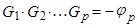
Тогда:
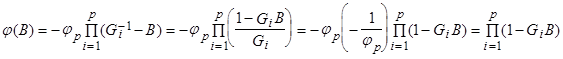
Следовательно, характеристическое уравнение
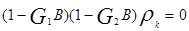 (12)
(12)
Для авторегрессии второго порядка:
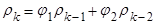
или 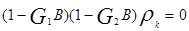 (13)
(13)
Производим замену переменных:
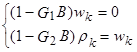 (14)
(14)
Тогда из первого уравнения (14) имеем:
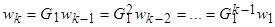 (15)
(15)
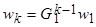
Из (14) 
Т.к. 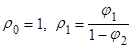 - это следует из выражения автокорреляционной функции для (АР,2)
- это следует из выражения автокорреляционной функции для (АР,2)
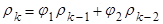
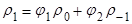
Т.к. 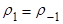 , то
, то 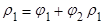 , отсюда
, отсюда
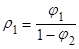
Следовательно, 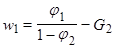
Выразим, используя теорему Виета, 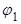 и
и 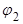 через
через 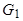 и
и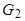 ;
;  , тогда
, тогда 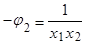
или 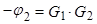
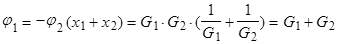 , т.е.
, т.е.
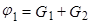
Следовательно, 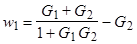 (*)
(*)
Из второго уравнения (14) 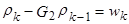 ,
,
или, используя рекуррентный характер соотношения:
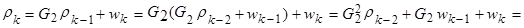
= … используя (15) … =
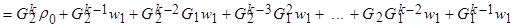 (16)
(16)
Далее используем (*) для 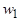
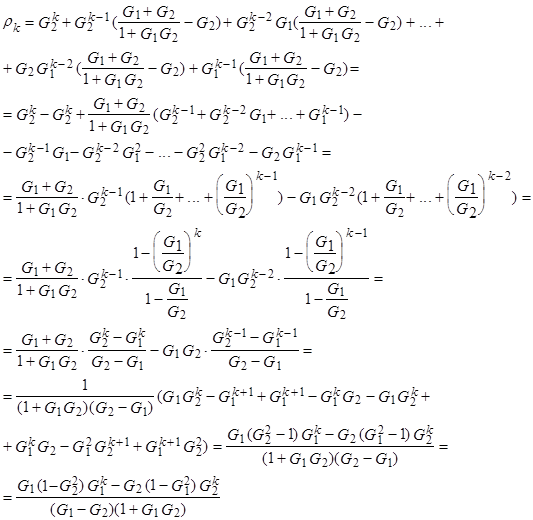
Итак, 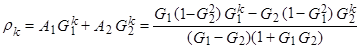 (17)
(17)
причем  - корни характеристического уравнения (1)
- корни характеристического уравнения (1) 
Когда корни действительны, автокорреляционная функция состоит из совокупности затухающих экспонент. Это происходит, когда 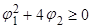 и соответствует областям 1 и 2, лежащим выше параболической границы. Конкретнее: в области 1 автокорреляционная функция затухает, оставаясь положительной, что соответствует положительному доминирующему корню [G] в (17). В области 2 затухающая функция автокорреляции знакопеременна, что соответствует отрицательному доминирующему корню [G].
и соответствует областям 1 и 2, лежащим выше параболической границы. Конкретнее: в области 1 автокорреляционная функция затухает, оставаясь положительной, что соответствует положительному доминирующему корню [G] в (17). В области 2 затухающая функция автокорреляции знакопеременна, что соответствует отрицательному доминирующему корню [G].
Если корни  - комплексные (
- комплексные (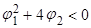 ), процесс авторегрессии второго порядка ведет себя как псевдопериодической.
), процесс авторегрессии второго порядка ведет себя как псевдопериодической.
Это поведение отражается на функции автокорреляции, т.к. заменой 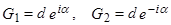 , если в уравнении 2 корня, и один - сопряженный, то другой - комплексно-сопряженный) получаем:
, если в уравнении 2 корня, и один - сопряженный, то другой - комплексно-сопряженный) получаем:
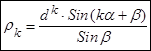 (18)
(18)
Комплексное число можно представить как

Т.к. 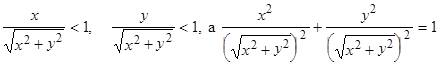 , то существует такой угол
, то существует такой угол 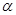 , что
, что 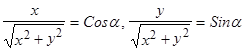 , т.е.
, т.е.
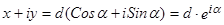
(т.к. 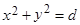 - длина вектора).
- длина вектора).
Тогда комплексно-сопряженное число 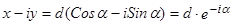 .
.
Делаем замену переменных в (17): 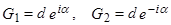 . Тогда
. Тогда
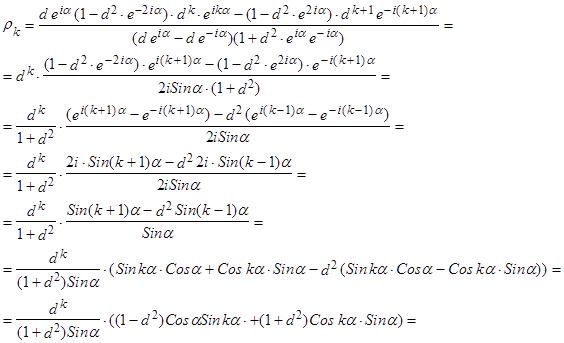
Умножим и разделим это выражение на 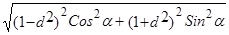 :
:
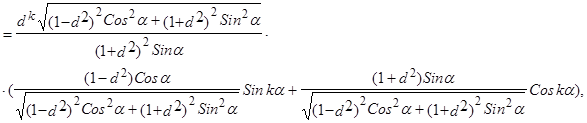
Тогда существует такой угол 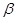 , что
, что
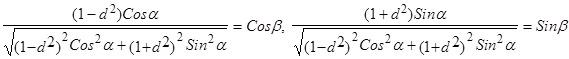 ,
,
Тогда
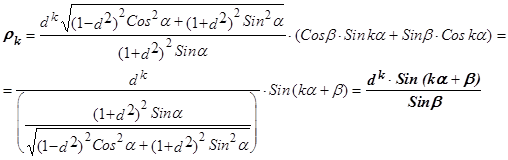 (18)
(18)
Нетрудно заметить, что 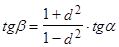 (19)
(19)
Стало быть, зная 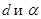 , можно найти
, можно найти 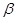 ;
; 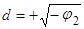 .
.
Действительно, известно, что (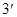 ):
): 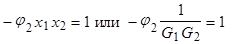
Отсюда 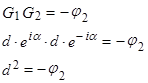
Следовательно, 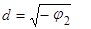 (20)
(20)
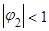 , следовательно
, следовательно 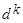 - затухающий коэффициент,
- затухающий коэффициент,
а для случая комплексных корней (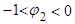 ) см. (8)
) см. (8)
Наконец, 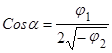 (21)
(21)
На самом деле, из (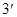 ) имеем:
) имеем:
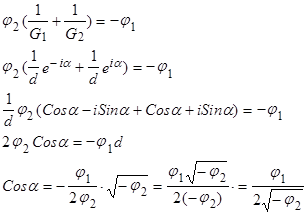
Выражение (18) показывает, что коррелограмма (или автокорреляционная функция) в процессе Юла является затухающей синусоидой.
Здесь появляются новые ограничения на 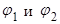 :
:
1. 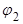 должно быть отрицательным, чтобы d было действительным
должно быть отрицательным, чтобы d было действительным
 (
(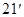 )
)
2. т.к. 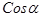 не может быть больше 1, то
не может быть больше 1, то
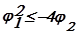 (22)
(22)
3. 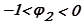 (
( )
)
4. Тогда 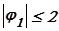 (23)
(23)
В противном случае ряд не будет колебаться в определенных пределах, а будет неограниченно расходиться.
Итак, в области 3 и 4 автокорреляционная функция - затухающая синусоида
Попробуем очертить область допустимых значений для 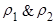 .
.
– Конец работы –
Эта тема принадлежит разделу:
АВТОРЕГРЕССИЯ ВТОРОГО ПОРЯДКА
На сайте allrefs.net читайте: "АВТОРЕГРЕССИЯ ВТОРОГО ПОРЯДКА"
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: ПРОЦЕСС ЮЛА
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов