ПРОЦЕСС АВТОРЕГРЕССИИ - ПРОИНТЕГРИРОВАННОГО СКОЛЬЗЯЩЕГО СРЕДНЕГО

Рассмотрим свойства важнейшего класса моделей, в которых d-я разность есть стационарный (смешанный) процесс авторегрессии - скользящего среднего. Эти модели называются процессами авторегрессии - проинтегрированного скользящего среднего (АРПСС)

Введем еще один важный оператор - разностный оператор со сдвигом назад (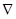), который можно выразить через В (оператор сдвига назад) как

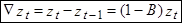
При этом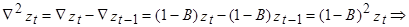

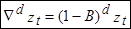(1)

В свою очередь оператор, обратный 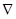, - это оператор суммирования S, выражаемый как

()

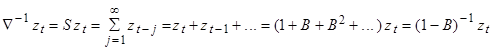
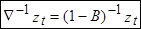Мы видели, что процесс АРСС стационарен, если корни уравнения 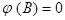лежат вне единичного круга, и нестационарен, если корни лежат внутри единичного круга.

Единственный нерассмотренный возможный случай - когда корни уравнения 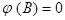лежат на единичной окружности. Оказывается, что соответствующие модели очень важны, т.к. позволяют описывать однородные нестационарные временные ряды. В частности, несезонные ряды могут нередко хорошо описываться моделями, у которых один или несколько корней равны единице.

БОКС И ДЖЕНКИНС решают проблему исключения тренда путем перехода к разностям ряда, и их модель соответствует предположению, что d-я разность ряда может быть представлена стационарным обратимым процессом АРСС.

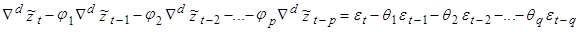(2)

Эту модель можно представить иначе (3):

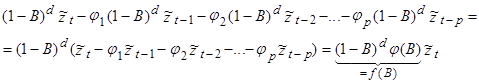
Следовательно, 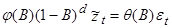(3)

где , и тогда

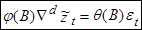(4)

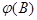- стационарный оператор авторегрессии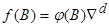

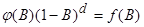- нестационарный оператор авторегрессии, такой, что d корней уравнения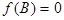 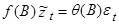равны единице, а остальные лежат вне единичного круга.

Так как , модель (4) можно представить в виде

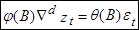(5)

Эквивалентное определение процесса можно дать двумя уравнениями:

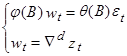(6)

Т.е. мы видим, что модель Бокса-Дженкинса соответствует предположению, что d-я разность ряда может быть представлена стационарным обратимым процессом АРСС.

Другой способ трактовки этого процесса при 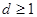получим, обратив :

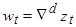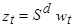(7)

где S - бесконечный оператор суммирования, определенный как

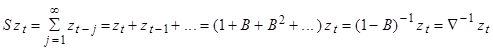
Таким образом,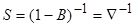

Оператор 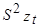определен аналогично:

(?)

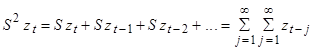Далее 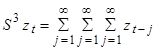и т.д.

Уравнение (7) показывает, что процесс (5) можно получить суммированием (или интегрированием) процесса (6) d раз. Поэтому процесс (5) мы будем называть процессом аиторегрессии - проинтегрированного скользящего среднего (АРПСС).

Как указывалось в лекции 3, модель (5) эквивалентна описанию процесса 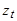, как выхода линейного фильтра (если 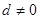, это неустойчивый линейный фильтр), на входе которого белый шум .

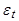Иначе мы можем рассматривать его как средство для преобразования сильно зависимых и, возможно, нестационарных членов 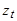процесса в последовательность некоррелированных случайных переменных 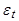, т.е. для преобразования процесса в белый шум.

Если в (5) оператор авторегрессии имеет порядок р, взята d-я разность и оператор скользящего среднего 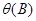имеет порядок q, мы говорим, что имеем модель АРПСС порядка (p,d,q) или просто АРПСС (p,d,q).

Когда d=0, модель (5) описывает стационарный процесс. Требования стационарности и обратимости накладываются независимо, и в общем случае операторы 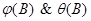имеют разные порядки.

Оператор 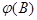- стационарен, т.е. корни уравнения 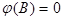лежат вне единичного круга. Оператор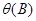предполагается обратимым, т.е. корни 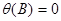лежат вне единичного круга.