Тема 4. Линейное пространство
Тема 4. Линейное пространство
1о. Определение и простейшие свойства
Пусть даны поле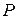 
с элементами, называемыми скалярами и обозначаемыми малыми греческими буквами 
, 
, 
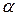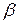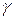, … и множество 
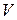элементов, называемых векторами и обозначаемых латинскими буквами 
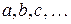. Введем на 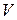алгебраическую операцию сложения, которая каждой паре элементов 
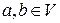ставит в соответствие третий элемент 
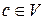, называемый суммой 
и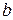 
и обозначаемый 
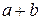, а также операцию умножения скаляра на вектора, которая
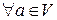и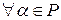 
ставится в соответствие 
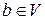, называемый произведением вектора на скаляр 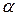и обозначаемый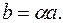 
Определение 1. Множество 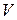вместе с заданными на нем операциями сложения векторов и умножения вектора на скаляр называется линейным (векторным) пространством над полем 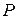, если удовлетворяются следующие аксиомы:
1) 
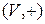является абелевой группой;
2) Для любых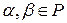 
и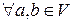
выполняются равенства:
а) Умножение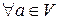 
на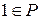 
не изменяет 
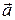, т.е. 
.
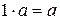б)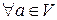 
.
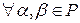
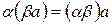в) Умножение вектора на скаляр дистрибутивно относительно сложения скаляров, т.е.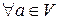 
.
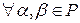
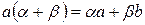г) Умножение вектора на скаляр дистрибутивно относительно сложения векторов, т.е.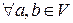 
.
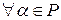
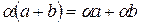Обозначение. .
Свойства линейного пространства. 1) выполняется . 2) выполняется .Примеры.
1) Если 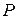− поле и 
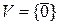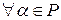, то имеем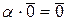 
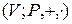− векторное пространство, называемое нулевым.
2) 
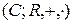− векторное пространство комплексных чисел над полем вещественных чисел. 
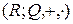− векторное пространство вещественных чисел над полем рациональных чисел.
3) Множество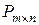 
матриц размера 
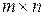образует векторное пространство 
.
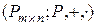4) Множество многочленов степени не выше n образует векторное пространство 
.
5) Множество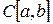 
непрерывных на 
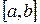функций образует векторное пространство 
.
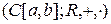6) 
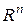– n-мерное координатное пространство (или арифметическое пространство), элементами которого являются упорядоченные наборы из n чисел: 
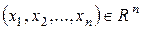. Операции определены следующим образом:
;
.
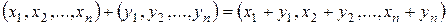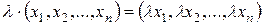Задача. Проверить выполнение аксиом векторного пространства.
2о. Линейно зависимые и линейно независимые системы векторов
Это понятие является обобщением понятия линейной зависимости строк.
Определение 2. Линейной комбинацией векторов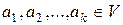 
с коэффициентами 
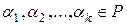называется выражение вида: 
.
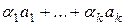Определение 3. Вектора 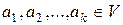называются линейно независимыми, если 
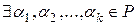, из которых хотя бы одно отлично от нуля, т.е. линейная комбинация 
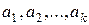с этими 
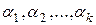является нулевым вектором V, т.е. 
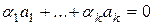. Вектора 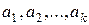, не являющиеся линейно зависимыми, называются линейно независимыми. Другими словами, 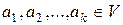называются линейно независимыми, если их линейная комбинация является нулевым элементом V лишь при условии, что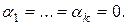 
Теорема 1.
2) Если среди один элемент нулевой, то они линейно зависимы. 3) Если часть элементов множества линейно зависима, то и все элементы линейно…Доказательство.
2. Если и – любое, например, линейно зависимы. 3. Если – линейно зависимы, то одновременно неравные нулю, так что и хотя бы… Пример. Рассмотрим линейное пространства и докажем, что n элементов из вида , ,…, линейно независимы, а добавление еще…Свойства изоморфных пространств.
Доказательство: Если . 2. Если элементам соответствуют , то линейная комбинация векторов равна нулю… Доказательство следует из 1.Как пример линейного пространства
1о. Направленные отрезки.
Рассмотрим в пространстве две точки А и В. Они определяют отрезок АВ.
Определение 1.Отрезок АВ называется направленным, если его концы А и В упорядочены; если при этом первой является точка А, а второй – точка В, то А – начало отрезка, а В – его конец.
Направленный отрезок обозначается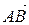 
или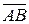 
. На чертеже направленный отрезок снабжен стрелкой на конце(см. рис.1)
Определение 2.Длиной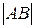 
направленного отрезка 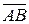называется длина отрезка АВ.
 |
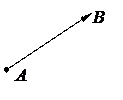Рис.1. Направленный отрезок АВ.
Определение 3.Направленные отрезки 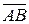и 
называются сонаправленными (обозначается 
), если они лежат на параллельных прямых и направлены в одну сторону.
Направленные отрезки и называют противоположно направленными (пишут 
), если они лежат на параллельных прямых и направлены в разные стороны.
Направленные отрезк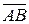и и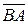 
называются противоположными.
Каждую точку А пространства можно рассматривать как направленный отрезок с совпадающим началом и концом. Этот отрезок обозначается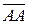 
и называется нулевым направленным отрезком. Его длина считается равной нулю, а направление не определено.
Определение 4.Два направленных отрезка 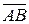и 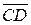считаются эквивалентными, если они сонаправлены и имеют равные длины. (Обозначают 
).
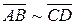Эквивалентность является отношением эквивалентности в множестве всех направленных отрезков, т.к. из определения эквивалентности следует:
1) отрезок 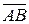эквивалентен сам себе;
2) если 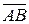эквивалентен 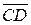, то 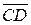эквивалентен ;
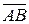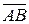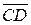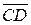3) если эквивалентен и эквивалентен 
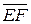, то 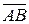эквивалентен .
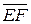Так как эквивалентность направленных отрезков является отношением эквивалентности, то множество всех направленных отрезков пространства разбивается на непересекающиеся классы – классы эквивалентности. Классы эквивалентности образуют фактор-множество множества всех направленных отрезков пространства.
Определение 5.Множество всех эквивалентных направленных отрезков называется вектором (или свободным вектором).
Замечание. Напомним, что в средней школе вектор характеризуетпараллельный перенос.
Направление эквивалентных направленных отрезков называется направлением вектора, а их длина – длиной вектора.
Таким образом, любой направленный отрезок однозначно определяет вектор, а вектор – это класс эквивалентных направленных отрезков.
Поэтому часто будем пишут вектор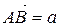 
, 
.
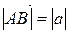Определение 6.Вектор a такой, что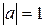 
называется единичным вектором или ортом. Множество нулевых отрезков называется нулевым вектором 
; Его длина равна нулю, а направление не определено.
Определение 7.Два ненулевых вектора, направления которых совпадают или противоположны, называются коллинеарными. Обозначают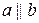 
.
Нулевой вектор считается коллинеарным любому вектору.
Очевидно, что прямые, на которых лежат представители классов коллинеарных векторов, параллельны.
Определение 8.Три и более векторов называются компланарными, если они параллельны некоторой плоскости.
Для определенности любую тройку векторов, содержащую нулевой вектор, считают комплонарной.
Пусть даны два вектора a и b. Из произвольной точки O пространства отложим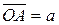 
и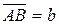 
. Тогда 
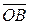есть направленный отрезок и значит, определяет вектор.
Покажем, что вектор 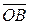не зависит от выбора точки O. Для этого выберем другую точку 
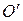. Пусть 
, 
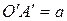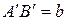. Тогда 
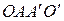– параллелограмм; аналогично, 
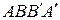– параллелограмм 
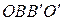– параллелограмм 
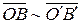, т.е. они определяют один и тот же вектор.
Определение 9.Вектор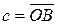 
называется суммой векторов и 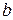. Пишут: 
.
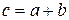Способ сложения векторов, изложенный выше, называется правилом треугольника. Можно также использовать правило параллелограмма.
Свойства сложения векторов.
2. . 3. , т.к. . 4. Для каждого вектора вектор, называемый вектором, противоположным , такой, что . Доказательство свойств может быть…Свойства умножения вектора на число.
2) и вектора . 3) и вектора . 4) вектора .Свойства проекции.
.Свойства скалярного произведения.
Действительно, (т.к. , т.е. четная функция, то ) . 2) Скалярное произведение двух векторов равно длине одного вектора умноженной… Действительно, .Построение вектора векторного произведения.
1. Через точку проведем плоскость . 2. Спроецируем на П точку . Получим вектор . 3. Далее повернем вектор по часовой стрелке на угол p/2 (если смотреть из конца вектора ) и получим вектор .Свойства векторного произведения.
Доказательство: Пусть и Þ Þ т.к. , Þ Þ , т.е. ||. Пусть ||, тогда Þ Þ .Вычисление векторного произведения в прямоугольных координатах
Þ очевидно, из коллинеарности. . Из этого следует, что . (см. рисунок).Свойства смешанного произведения.
Доказательство: Отложим вектора , , из одной точки. Возможны две ситуации: a) Тройка , , – правая; б) Тройка , , – левая.Вычисление смешанного произведения в прямоугольных координатах.
Тогда . ,Решение.
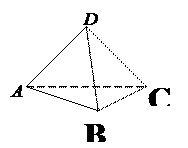
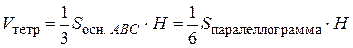. Но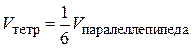 
.
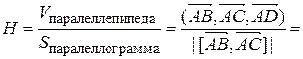
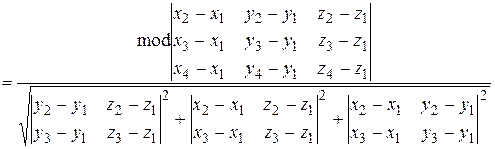