Лекция 1. Начала теории множеств.

Цель: Изучить основные понятия теории множеств.

План:

1. Понятие множества

2. Операции над множествами.

3. Отображения множеств.

3. Вопросы для контроля знаний и подведения итога прочитанной лекции

1. Понятие множества. Множество — это совокупность, собрание каких-либо объектов, объединяемых общим признаком или свойством. Эту фразу нельзя рассматривать как определение понятия «множество», так как в ней слово «множество» заменено столь же неопределенным термином «совокупность». Так, можно говорить о множестве всех студентов данного курса, о множестве телевизоров с цветным изображением в данной аудитории, о множестве всех натуральных чисел и т.д. Объекты, входящие в данное множество, будем называть элементами множества.

Множества будем обозначать прописными (большими) латинскими буквами А, В, С, ... , X, Y, ... , а их элементы — малыми буквами а, b, с, ..., х, у, ... .

Если элемент а является элементом множества А, то пишут а Î А (читается «а принадлежит А», или «а из А»). В этом случае говорят также, что «а содержится в А», «а входит в А» и т. п.

Если а не является элементом множества А, то будем писать аÏ А («а не принадлежит А» или «а не содержится в А» и т.д.).

Если элементами множества являются числа, то оно называется числовыми.

Многие из числовых множеств имеют специальные названия и обозначения. Таковы, например, сегмент, или отрезок [а, Ь], по­луинтервалы [а, b) и (а, b] (см. подразд. 2.1, п. 1).

Множество всех целых положительных чисел 1, 2, 3, ... n, ... называют натуральным рядом и обозначают N.

Множество всех действительных чисел обозначают R, или (-∞, +∞) (см. подразд. 2.1, п. 1).

Если множество содержит лишь конечное число элементов, то оно называется конечным. В противном случае множество называется бесконечным. Например, множество листьев на дереве или множество слушателей в данной аудитории — конечные множества; множество точек на плоскости — бесконечное множество. Числовые множества N, R,, [а, b] (при а ≠ b] также бесконечны.

Существуют разные формы задания множества. Наиболее простая состоит в указании всех элементов множества. Так, запись A = {1, 2, 3} означает, что множество A состоит из трех элементов 1, 2 и 3. Если число элементов бесконечно, то используется многоточие. Например, множество всех натуральных чисел записывается так: N= {1, 2, 3,...}. Иной способ задания множества состоит в описании элементов определяющим свойством Р(х) (формой от х), общим для всех элементов А = {х: Р(х)}. Например, А = {х: х = 2k, k = 1, 2, ...} означает, что множество А состоит из четных положительных целых чисел 2, 4, 6, ... .

Если множества А и В состоят из одних и тех же элементов, т. е. если каждый элемент множества А является элементом множества В и, наоборот, каждый элемент множества В является элементом множества A, то множества А и В равны (тождественны, совпадают). Таким образом, множество однозначно определяется своими элемен­тами и не может содержать одинаковых элементов. Если множества А и В равны, то пишут А = В. Например, {1, 2} = {2, 1}.

Пусть теперь имеются два множества А и В, относительно которых известно только, что каждый элемент множества В является элементом множества А. В этом случае говорят, что В есть подмножество А, и пишут В ÌА (“Ì “ - знак включения). Говорят еще, что «А содержит В» или «В включено в А». В частности, В может совпадать с А.

Пример 11.1.Множество четных чисел есть подмножество множества целых чисел.

Теорема 11.1. Если В Ì А и А Ì В, то А = В.

Доказательство. Из В Ì А следует, что любой элемент из В является элементом множества А, а из А Ì В — что любой элемент из А является элементом множества В, т.е. множества А и В состоят из одних и тех же элементов и, значит, А = В.

Обычно приходится рассматривать множества А, В, С и т.д., которые являются подмножествами некоторого достаточно обширного множества, рамки которого определяются целями нашего исследования. Такое исходное множество называется универсальным и обозначается через U. Если изучаются всевозможные числовые множества, то универсальным будет множество всех действительных чисел.

Множество, не содержащее ни одного элемента, называется пустым. Его обозначают Æ. Примерами пустого множества могут служить: множество людей на Солнце, множество действительных корней уравнения х² + 1 = 0.

Теорема 11.2. Пустое множество является подмножеством любого множества А.

Доказательство. Из определения подмножества следует, что В является подмножеством А, если В не содержит элементов, не являющихся элементами А. Но пустое множество не содержит ни одного элемента, поэтому оно не содержит и элементов, не принадлежащих А. Отсюда следует, что пустое множество есть подмножество любого множества А.

2. Операции над множествами.Пусть даны два множества А и В.

Определение 1. Объединением (или суммой) этих множеств называется множество С, состоящее из всех тех элементов, которые принадлежат хотя бы одному из множеств А или В.

Обозначается: С = А È В (или С = А + В). Знак «È» называется знаком объединения.

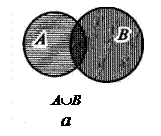
На рис. 11.1 изображены два множества точек плоскости: круг А и круг В. Их объединение — это область, покрытая или горизонтальной, или вертикальной штриховкой.

Заметим, что А È А = А. В общем случае А с А и В так же, как и В с А и В.

Пример 11.2. {1, 2, 3}È{2, 3, 4} = {1, 2, 3, 4}.

Определение 2. Пересечением (или произведением) множеств А и В называется множество С, состоящее из всех тех элементов, которые принадлежат и множеству А, и множеству В.

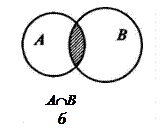
Обозначается: С = А Ç В (или С = А В). Знак Ç называется знаком пересечения. На рис. 11.1 пересечение множеств А и В — это область покрытая и горизонтальной, и вертикальной штриховкой.

Заметим, что А Ç А = А. В общем случае (А Ç В) Ì А и (А Ç В) Ì В.

Пример 11.3. {1, 2, 3} п {2, 3, 4} = {2,3}.

Рис. 11.3

 

	Рис. 11.4

 

Для некоторой пары множеств может оказаться, что их пересечение — пустое множество. Так, например, {1, 2, 3} Ç {5, 6, 7} = Æ. Пустым будет и пересечение множеств А и B, изображенных на рис. 11.2.

Множества, пересечение которых пусто, называются непересекающимися.

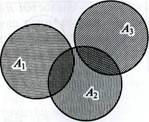
Введенные операции объединения и пересечения множеств легко обобщаются на большее чем два число множеств. Так, множество С называется объединением множеств А₁ ÈА₂ È ... А_п, если С состоит из всех тех элементов, которые принадлежат хотя бы одному из множеств А_k, k=1,2,..., п. Обозначается С = А₁ ÈА₂ È ... А_п , или кратко С = 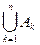. На рис. 11.3 изображено объединение множеств А₁, А_2,, A₃ (вся заштрихованная область).

Аналогично множество С называется пересечением или общей частью множеств А_ь А₂,..., А„, если оно состоит из всех тех элементов, которые принадлежат всем множествам А_k,, к =1, 2,..., п. Обозначается С = А₁ ÇА₂Ç ... А_п или кратко С = .

На рис. 11.4 пересечение множеств А_ь А_2> А₃ — область, покрытая тройной штриховкой.

Введем еще одну операцию — вычитание множеств. Пусть имеются два множества А и В.

Определение 4. Разностью множеств А и В называется совокупность тех элементов множества А, которые не являются элементами множества В.

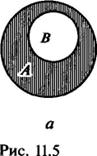
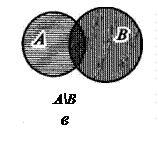
Разность множеств А и В обозначается АВ. При этом В может содержаться в множестве А полностью, частично или совсем не включаться. На рис. 11.5, а — в изображены эти три случая. Разность АВ каждый раз заштрихована. Заметим, что в последнем случае, т. е. когда А Ç В = Æ, разность АВ = А. В общем случае АВ Ì А.

в

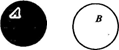б