МЕХАНИКА
МЕХАНИКА
Лекция 1
Материальной точкой называют тело, размерами которого можно пренебречь по… К телам больших (по сравнению с массой атомов) масс и малых (по сравнению со скоростью света) скоростей можно считать…Средняя скорость .
Средняя путевая скорость .
Модуль скорости . В системе СИ скорость имеет размерность – м/с . В проекциях на координатные осиЛекция 2
Силы Силой называется векторная величина, характеризующая воздействия на рассматриваемое тело со стороны других тел, в…Однородная сила тяжести: .
, где – ускорение свободного падения; – ускорение тела вместе с опорой относительно Земли.Лекция 3
Закон сохранения момента импульса
, где – радиус-вектор, проведённый из точки О в точку А приложения силы.JO = JC + m.а 2 .
Доказательство теоремы:

Пусть положение i-го элемента твёрдого тела относительно осей О и С характеризуется векторами  и
и  , а положение оси С относительно оси О – вектором
, а положение оси С относительно оси О – вектором  , плоскость которого перпендикулярна осям О и С . Воспользовавшись связью между этими векторами
, плоскость которого перпендикулярна осям О и С . Воспользовавшись связью между этими векторами 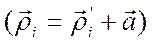 , преобразуем выражение для момента инерции тела относительно оси О следующим образом:
, преобразуем выражение для момента инерции тела относительно оси О следующим образом:
 , или
, или

 .
.
В правой части этого равенства первая сумма представляет собой момент инерции тела JC i-го элемента твёрдого тела относительно оси С, а последняя сумма равна m.а 2. Покажем, что средняя сумма равна нулю.
Пусть 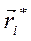 – радиус-вектор i-го элемента твёрдого тела относительно центра масс, тогда относительно центра масс суммарный вектор
– радиус-вектор i-го элемента твёрдого тела относительно центра масс, тогда относительно центра масс суммарный вектор 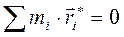 . Но
. Но  – это составляющая вектора
– это составляющая вектора  , перпендикулярная осям О и С . Очевидно, что если суммарный вектор равен нулю, то сумма его составляющих в плоскости, перпендикулярной осям О и С , также равна нулю, т.е.
, перпендикулярная осям О и С . Очевидно, что если суммарный вектор равен нулю, то сумма его составляющих в плоскости, перпендикулярной осям О и С , также равна нулю, т.е. 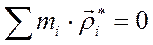 и теорема доказана.
и теорема доказана.
Моменты инерции некоторых однородных твёрдых тел:
| Тело | Положение оси | Момент инерции |
| Обруч или полый тонкостенный цилиндр радиуса R и массы т | Ось обруча или цилиндра | mR2 |
| Сплошной цилиндр или диск радиуса R и массы т | Ось цилиндра или диска |
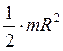
|
| Шар радиуса R и массы т | Ось проходит через центр шара |
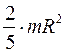
|
| Тонкостенная сфера радиуса R и массы т | Ось проходит через центр сферы | 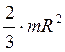
|
| Прямой тонкий стержень длины l и массы т | Ось перпендикулярна к стержню и проходит через его середину Ось перпендикулярна к стержню и проходит через его конец |

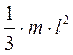
|
Основной закон динамики вращательного
движения
Выражение 2-ого закона Ньютона 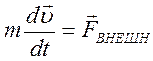 можно преобразовать, умножив левую и правую часть на
можно преобразовать, умножив левую и правую часть на 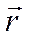 :
:
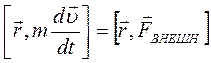 или
или 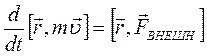 или
или

Рассмотрим вращение твёрдого тела вокруг оси OZ.

Момент импульса твёрдого тела относительно начала координат (точки О)
 .
.
Вектор  перпендикулярен оси
перпендикулярен оси  , а вектор
, а вектор  направлен вдоль оси OZ. Таким образом ,
направлен вдоль оси OZ. Таким образом ,  или
или
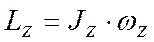 .
.
Тогда
 .
.
Если тело в процессе вращения не деформируется, то  и
и
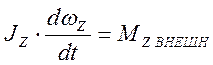 или
или
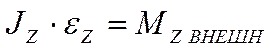 , где
, где
 – проекция вектора углового ускорения
– проекция вектора углового ускорения 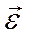 на ось вращения OZ.
на ось вращения OZ.
Для замкнутой (изолированной) системы момент внешних сил МВНЕШН всегда равен нулю, так как на неё внешние силы не действуют. Поэтому из основного закона динамики вращательногодвижения (закона изменения момента импульса) вытекает закон сохранения момента импульса:
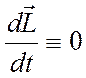 и
и 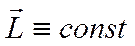 .
.
Момент импульса замкнутой системы относительно неподвижной точки не изменяется с течением времени.
Если за неподвижную точку взять центр масс системы, то для замкнутой системы 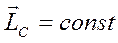 .
.
Момент импульса замкнутой системы относительно любой неподвижной оси OZ также всё время остаётся постоянным:
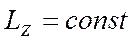 .
.
Если в незамкнутой системе сумма моментов относительно какой-либо неподвижной оси всех внешних сил, действующих на систему, тождественно равен нулю, то момент импульса системы относительно этой оси не изменяется с течением времени. Т.е. если 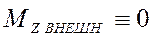 , то
, то  .
.
Пример: Скамья Жуковского
Скамья Жуковского представляет собой горизонтальную площадку, имеющую форму круга и свободно вращающуюся без трения вокруг неподвижной вертикальной оси OZ . Человек, стоящий на скамье, держит в руках массивные гимнастические гантели и вращается вместе со скамьёй вокруг OZ .
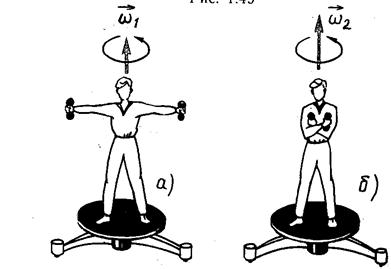
Прижимая гантели к груди, человек уменьшает момент инерции системы, и угловая скорость её вращения возрастает.
Поскольку момент внешних сил (сил тяжести и реакции подшипников скамьи) относительно оси OZ равен нулю, момент импульса системы относительно оси OZ в рассматриваемом процессе не изменяется, т.е.
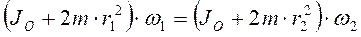 . где
. где
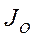 – момент инерции человека и скамьи;
– момент инерции человека и скамьи;
т – масса одной гантели.
Лекция 4
Работа. Рассмотрим малое перемещение , в пределах которого силу , действующую… В механике вводится понятие элементарной работы силы на перемещение:Консервативные силы
. Работа консервативной силы на произвольной замкнутой траектории l точки её приложения равна нулюПотенциальная энергия
Работа А1-2 , совершаемая консервативными (потенциальными) силами при изменении конфигурации системы , т.е. расположения её частей (материальных… A1-2 = W1 – W2.Пример 1. Потенциальная энергия материальной точки в однородном поле силы тяжести.
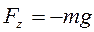 ;
;
h – высота подъёма тела над поверхностью Земли ;
W0 = 0 на поверхности Земли.

 .
.
Пример 2. Потенциальная энергия упруго деформируемого тела.
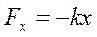 по закону Гука ;
по закону Гука ;
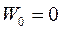 при х = 0 (для недеформированного тела);
при х = 0 (для недеформированного тела);
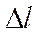 – деформация (удлинение или сжатие деформируемого тела).
– деформация (удлинение или сжатие деформируемого тела).
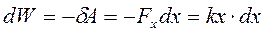
 .
.
Пример 3. Потенциальная энергия материальной точки в поле центральных сил.
Силы, действующие на материальную точку, называются центральными, если они зависят только от расстояния между материальной точкой и некоторой неподвижной точкой – центром силы – и направлены всюду от центра силы либо всюду к центру силы. Если центр силы принять за начало координат, то центральная сила
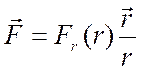 , где
, где
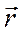 – радиус вектор, проведённый из центра силы в рассматриваемую точку поля;
– радиус вектор, проведённый из центра силы в рассматриваемую точку поля;
 – расстояние от точки до центра силы;
– расстояние от точки до центра силы;
 – проекция силы
– проекция силы  на радиус-вектор
на радиус-вектор  .
.
Для сил отталкивания  ;
;
Для сил притяжения 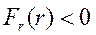 .
.
Докажем, что поле центральных сил потенциально:
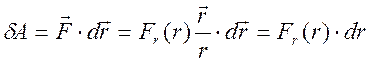 т.к.
т.к.  и
и
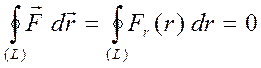 .
.
Найдём потенциальную энергию материальной точки:
 .
.
Обычно полагают, что  . Тогда
. Тогда
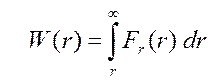 .
.
а) для гравитационного поля материальной точки или однородного шара 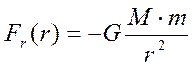 , где
, где
М – масса материальной точки или однородного шара, создающих гравитационное поле;
т – масса материальной точки, находящейся в рассматриваемом поле.

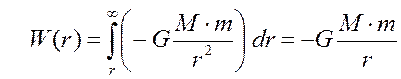 .
.
б) для электростатического поля точечного электрического заряда или равномерно заряженных шара или сферы  .
.
 .
.
Механической энергией системы называют величину Е , равную сумме кинетической и потенциальной энергий системы:
E = K + W .
Изменение механической энергии системы равно алгебраической сумме работ всех неконсервативных сил, действующих на систему, и изменения потенциальной энергии системы за рассматриваемый промежуток времени, обусловленного нестационарностью внешних консервативных сил
 .
.
Если система замкнута то  .
.
Закон сохранения механической энергии: механическая энергия замкнутой системы не изменяется, если все внутренние силы консервативные (потенциальные) либо не совершают работы (например, силы трения покоя и гироскопические силы работы не совершают).
Сопоставление формул механики поступательного движения и вращения вокруг неподвижной оси
| Поступательное движение | Вращение |
 – линейная скорость – линейная скорость
|  – угловая скорость – угловая скорость
|
 – линейное ускорение – линейное ускорение
|  – угловое ускорение – угловое ускорение
|
| т – масса | J – момент инерции |
 – импульс – импульс
|  – момент импульса – момент импульса
|
 – сила – сила
|  – момент силы – момент силы
|
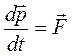 или или 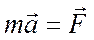 – уравнение движения – уравнение движения
|  или или  – уравнение движения – уравнение движения
|
 – кинетическая энергия – кинетическая энергия
| 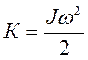 – кинетическая энергия – кинетическая энергия
|
 – работа – работа
| 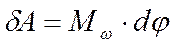 – работа – работа
|
 – мощность – мощность
|  – мощность – мощность
|
Лекция 5
Колебания
Колебания называют периодическими если значения всех физических величин, характеризующих колебательную систему и изменяющихся при её колебаниях,… Т0 – период колебаний (наименьший промежуток времени, удовлетворяющий этому… – частота колебаний;А) сложение колебаний одного направления
Б) сложение взаимно перпендикулярных гармонических колебаний одинаковой частоты.
Пусть точка М одновременно колеблется вдоль осей координат ОХ и ОУ по законам: иСвободные незатухающие колебания
, тогда иE, K, W
 E
E
K
W
Линейный гармонический осциллятор – 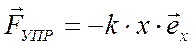 (например, пружинный маятник).
(например, пружинный маятник).
 или
или 
Это уравнение является дифференциальным уравнением гармонических колебаний, решением которого является
 ,
,
где 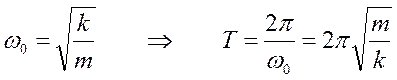


Импульс гармонического осциллятора
 .
.
Если из системы уравнений р(t) и x(t) исключить время то после преобразований приходим к уравнению, которое на координатной плоскости х, р (фазовой плоскости) является уравнением эллипса
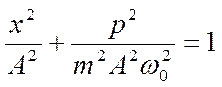 .
.
График зависимости р = р(х) называют фазовой траекторией. Любая точка этой траектории соответствует состоянию осциллятора в некоторый момент времени. Ниже представлены фазовые траектории свободных незатухающих колебаний, образующих семейство подобных эллипсов (отношение длин полуосей равно k2 ).

Каждому эллипсу соответствует определённый уровень энергии осциллятора. Площадь эллипса равна произведению его полуосей, умноженному на  :
:
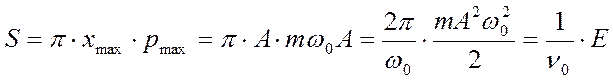 .
.
Следовательно, для полной энергии осциллятора можно записать 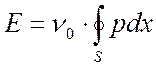 ,
,
где интеграл представляет из себя площадь, охватываемую фазовой кривой.
 Физический маятник – твёрдое тело, которое может вращаться под действием своей силы тяжести mg вокруг неподвижной горизонтальной оси О , не проходящей через центр масс тела и называемой осью качания маятника.
Физический маятник – твёрдое тело, которое может вращаться под действием своей силы тяжести mg вокруг неподвижной горизонтальной оси О , не проходящей через центр масс тела и называемой осью качания маятника.
Если пренебречь силами трения в подвесе маятника, то момент относительно оси качания создаёт только mg и при отклонении маятника на угол α эта сила создаёт момент численно равный 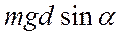 и стремящийся возвратить маятник в положение равновесия (α = 0).
и стремящийся возвратить маятник в положение равновесия (α = 0).
В соответствии с основным законом динамики твёрдого тела, вращающегося вокруг неподвижной оси, уравнение движения физического маятника имеет вид
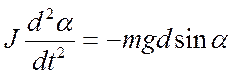 , где
, где
 – расстояние от центра масс маятника до оси качания;
– расстояние от центра масс маятника до оси качания;
J – момент инерции маятника относительно той же оси.
При малых колебаниях 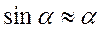 . Тогда
. Тогда

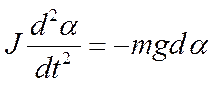 и угол α удовлетворяет дифференциальному уравнению гармонических колебаний
и угол α удовлетворяет дифференциальному уравнению гармонических колебаний
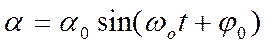 , где
, где
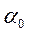 – амплитуда колебаний угла
– амплитуда колебаний угла 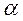 .
.
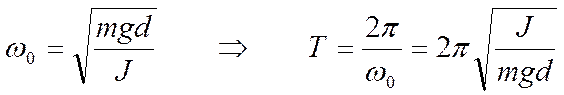
Математический маятник – предельный случай физического маятника – материальная точка, подвешенная на невесомой нерастяжимой нити и совершающая колебания в вертикальной плоскости под действием силы тяжести.
В этом случае d = l – длина математического маятника, а J = ml2.
Соответственно  .
.
Длина математического маятника, имеющего такой же период колебаний, что и данный физический маятник называется приведённой длиной lпр этого физического маятника
 .
.
Точка О1 , лежащая на прямой ОС на расстоянии lпр от точки подвеса О , называется центром качания физического маятника. Точки О и О1 обладают свойством взаимности.
Лекция 6
Свободные затухающие колебания
Свободные колебания реальных систем всегда затухают. Затухания свободных механических колебаний вызываются главным образом трением, сопротивлением… Система называется линейной если параметры, характеризующие существенные в… Пример: свободные затухающие колебания пружинного маятника массы т , движущегося в вязкой среде вдоль оси ОХ. На…И δ2 – корни характеристического уравнения .
, где – мнимая единица. Общее решение дифференциального уравнения затухающих колебаний имеет видВынужденные колебания
Переменная внешняя сила, приложенная к системе и вызывающая её вынужденные механические колебания, называется вынуждающей или возмущающей. Дифференциальное уравнение вынужденных колебаний гармонического осциллятора … , гдеЛекция 7
Механические волны
Среду называют упругой, а деформации, вызываемые внешними воздействиями, называют упругими деформациями, если они полностью исчезают после… Газу присуща объёмная упругость, т.е. способность сопротивляться изменению его… По закону Гука для объёмной деформацииЭнергия волны
Упругая среда, в которой распространяются механические волны, обладает как кинетической энергией колебательного движения частиц, так и потенциальной… Выбрав малый объём среды dV можно записать для плотности энергии , гдеИнтерференция волн
Рассмотрим наложение двух гармонических волн, возбуждаемых в однородной и изотропной среде точечными источниками S1 и S2 , с циклическими частотами…Лекции 8 и 9
Элементы релятивистской механики
В общем случае принцип относительности Галилея можно записать следующим образом: законы механики одинаковы во всех инерциальных системах отсчёта… После того как во второй половине ХIХ в. Максвеллом были сформулированы… В электродинамике Максвелла скорость распространения электромагнитных волн в вакууме одинакова по всем направлениям и…Пример с поездом
Световой сигнал из середины поезда для пассажира поезда (в системе отчёта К*) приходит в точки 1 и 2 одновременно, а для наблюдателя, находящегося на платформе (в системе отсчёта К) точка1 движется навстречу сигналу, а точку 2 сигналу приходится «догонять».

Таким образом в разных системах отсчёта время течёт неодинаково.
Чтобы описать «точечное» событие (например, распад элементарной частицы) нужно указать, в каком месте и в какой момент времени оно происходит. Эта задача может быть осуществимой, если создать в пространстве равноотстоящие координатные метки и совместить с каждой такой меткой часы. Синхронизацию часов можно сделать, посылая от одних часов к другим световой согнал.
Постоянство скорости света приводит к тому, что пространство и время оказываются взаимосвязанными, образуя единое пространство-время. Эта взаимосвязь может быть представлена в виде виртуального четырёхмерного пространства