рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Философия
- /
- Теоретична частина
Реферат Курсовая Конспект
Теоретична частина
Теоретична частина - раздел Философия, Теорія ймовірностей та математична статистика. ПРАКТИКУМ Математи́чна Інду́кція – Засто...
Математи́чна інду́кція – застосування принципу індукції для доведення теорем в математиці. Зазвичай полягає в доведенні вірності твердження стосовно одного з натуральних чисел, а потім всіх наступних.
Отже, загальна схема доведення по індукції така: є деяка послідовність тверджень (A1; A2; …; An;..). Ми доводимо, що чергове твердження (An) вірно, вважаючи відомим, що всі попередні твердження (Ak при k <n) вірні. Це дозволяє нам стверджувати, що всі твердження An вірні.
Такий спосіб міркування називається математичної індукцією, а величина n називається параметром індукції. Кажуть, що ми доводимо твердження An індукцією по n.
Принцип повної математичної індукції. Нехай є послідовність тверджень A1; A2; …; An. Якщо для будь-якого натурального n з того, що істинні всі A1; A2; …; An-1, слідує також істинність An, то всі твердження в цій послідовності істинні, тобто (" n Є N) (" i Є {1, 2, … , n-1} Ai®An) ®(" n Є N) An.
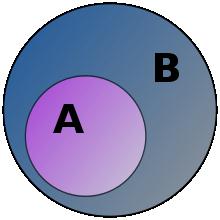
Принцип суми. Якщо множина A містить m елементів, а множина B – n елементів, і ці множини не перетинаються, то A Ư B містить m+n елементів.
Принцип добутку. Якщо об’єкт а можна обрати m – способами, та при кожному вибору об’єкту об’єкт bможна обрати n – способами, то вибір пари (а b) можна виконати m×n – способами.
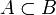
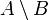
Розміщення без повторень. Кількість розміщень з n елементів по k обчислюють за формулою:
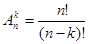
Перестановки без повторення. Число перестановок з n – елементів дорівнює добутку всіх натуральних чисел від 1 до n.
Pn=1*2*…*n=n!
Комбінації без повторень. Кількість комбінацій з n елементів по k обчислюють за формулою:
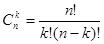
Розміщення з повторенням. За правилом множення кількість розміщень з повтореннями з n по k одне:
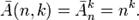
Перестановки з повторенням. Кількість перестановок з повтореннями з елементів множини A={a1, a2, …, an} складу (k1, k2, …, kn) позначається P(k1, k2, …, kn) і виражається формулою:
Комбінації з повторенням. Кількість комбінацій з повторенням з n–елементів по k обчислюють за формулою:
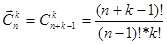
Приклад 1. Застосовуючи метод математичної індукції, довести, що для будь-якого натурального n>1 вірна така рівність:
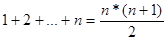
Розв’язок:
Базис індукції: При n=1 вірне твердження
При n=2
Крок індукції: Виділимо в сумі 1+2+3+..+( n-1)+ n останній член
(1+2+3+..+( n-1))+ n
За твердженням індукції праву частину можна переписати таким чином:
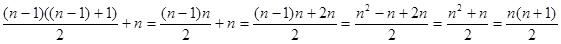
Що треба було довести.
Приклад 2. Існують множини A і B, які складаються з елементів:
A ={1, 2, 5, 8, 10}
B= {1, 3. 5, 9, 12}
Знайти: A∩B, A ∕ B, АUB.
Розв’язок:
A∩B. Слід обрати елементи, які присутні як в множині А так і в множині B:
A∩B={1, 5}
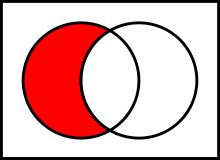
A∕B. Слід виписати такі елементи, які не співпадають з елементами як множини A так і множини B.
A∕B={2, 3, 8, 9, 10, 12}
АUB. Слід спочатку виписати елементи множини А, а потім дописати елементи множини B, яких не вистачає в множині А.
АUB={1, 2, 5, 8, 10, 3, 9, 12}
Приклад 3. Скількома способами можна зробити триколірний прапорець з горизонтальними смугами однакової ширини, якщо є тканина 6 різних кольорів?
Розв’язок:
Елементи у сполуцi не повторюються.
Кiлькiсть мiсць (m) у сполуцi менша за кiлькiсть елементiв (n), якi претендують на цi мiсця (m < n).
Порядок розташування елементiв у сполуцi має значення.
Задано 6 різнокольорових тканини, причому місць для цих тканин 3, тому що прапор складається з трьох кольорів. Порядок розташування має значення, тому обчислюємо за формулою:
A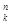
= 
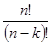
n=6
k=3
A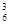
= 
= 
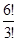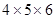= 120
Приклад 4. У шаховому турнірі беруть участь 7 чоловік. Скількома способами можуть розподілитись місця між ними?
Розв’язок:
Якщо участь у шаховому турнірі беруть 7 чоловік, то кількість місць, які можна між ними розподілити теж 7. Перше місце можна присудити одному з n, тобто 7-мі гравців, друге – одному з n-1, тобто з 6-ти гравців, третє – одному з n-2, тобто з 5-ти гравців і так далі. За правилом добутку отримаємо n*(n-1)*(n-2)*(n-3)*…*1= n!
Число всіх можливих перестановок з n-елементів можна розрахувати за формулою
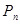= n!
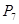= 7!
Приклад 5. У змаганнях з баскетболу беруть участь 10 команд, з яких тiльки чотири перших змагатимуться у фiнальнiй частинi. Скiльки iснує варiантiв складу фiнальної четвiрки?
Розв’язок: Не має значення, яке з чотирьох перших мiсць посяде команда. Усього 10 команд, кiлькiсть мiсць для фiналiстiв дорiвнює 4, отже, iснує
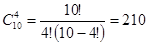варiантiв складу фiнальної четвiрки.
Приклад 6. На шкільному вечорі присутні 12 дівчат та 15 юнаків. Скількома способами можна вибрати з них 4 пари для танців?
Розв’язок:
Серед 12 дівчат слід обрати 4 для пари в танці, тобто
n1=12 к=4
Серед 15 юнаків теж слід обрати 4 пари для танців, тобто
n2=15 к=4
Для знаходження розв’язку слід знайти добуток комбінацій з
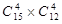
де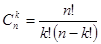 
Приклад 7. Скільки двоцифрових чисел можна скласти з цифр 1, 2, 3, 4, 5, 6?
Розв’язок: Задачу можна розв’язати двома способами. Розглянемо перший спосіб, тобто складемо всі можливі варіанти пар з шести чисел по 2, враховуючі, що числа можуть повторюватися.
(1,1) (1,2) (1,3) (1,4) (1,5) (1,6)
(2,1) (2,2) (2,3) (2,4) (2,5) (2,6)
(3,1) (3,2) (3,3) (3,4) (3,5) (3,6)
(4,1) (4,2) (4,3) (4,4) (4,5) (4,6)
(5,1) (5,2) (5,3) (5,4) (5,5) (5,6)
(6,1) (6,2) (6,3) (6,4) (6,5) (6,6)
Таким чином, ми отримали деяку матрицю, яка складається з 6-ти стовпців та рядків, використовуючи правило добутку можна отримати результат задачі 6*6=36.
Другий засіб набагато простіше, достатньо скористатися формулою про розміщення з повторенням:
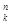= n
n=6
k=2
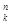=62=36
Приклад 8. Скільки різних слів можна утворити, переставляючи букви слова «Паралелограм»
Розв’язок. Розрахуємо скільки разів зустрічаються букви в слові «паралелограм»
п-1
а-3
р-2
л-2
о-1
г-1
м-1
е-1
Застосовуючи формулу перестановки з повторенням отримаємо:
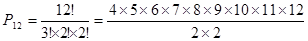
Приклад 9. У кондитерському магазині продавалися 4 сорти тістечок: еклери, пісочні, наполеони і листкові. Скількома способами можна купити 7 тістечок.
Розв’язок. Покупка не залежить від того, в якому порядку укладають куплені тістечка в коробку. Покупки будуть різними, якщо вони відрізняються кількістю куплених тістечок хоча б одного сорту. Отже, кількість різних покупок дорівнює числу сполучень чотирьох видів тістечок по сім.
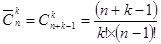
Приклад 10. У класі 35 учнів. З них 20 відвідують математичний гурток, 11- фізичний, 10 учнів не відвідують жодного з цих гуртків. Скільки учнів відвідують обидва гуртки? Скільки учнів відвідують лише математичний гурток?
– Конец работы –
Эта тема принадлежит разделу:
Теорія ймовірностей та математична статистика. ПРАКТИКУМ
Первомайський політехнічний коледж... Первомайського політехнічного інституту... Національного університету кораблебудування ім адмірала Макарова...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Теоретична частина
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?
Подпишитесь на Нашу рассылку
Реклама
Информация в виде рефератов, конспектов, лекций, курсовых и дипломных работ имеют своего автора, которому принадлежат права. Поэтому, прежде чем использовать какую либо информацию с этого сайта, убедитесь, что этим Вы не нарушаете чье либо право.
© copyright 1999 - 2024 allRefs.net. Все права защищены. Страница сгенерирована за: 0.022 сек.
Новости и инфо для студентов