рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Компьютеры
- /
- Уравнение касательной и нормали к плоской кривой
Реферат Курсовая Конспект
Уравнение касательной и нормали к плоской кривой
Уравнение касательной и нормали к плоской кривой - раздел Компьютеры, Непрерывность функции. Точки разрыва. Асимптоты графика функции У1 ...
|
|



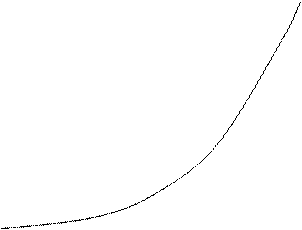



Пусть дана кривая L, заданная уравнением 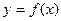 . Возьмем на ней фиксированную точку Мо(х0;у0). Если точка М1(х1;у1) тоже принадлежит кривой L, то прямая М0 М1 называется секущей. Будем перемещать М1 вдоль L так, чтобы
. Возьмем на ней фиксированную точку Мо(х0;у0). Если точка М1(х1;у1) тоже принадлежит кривой L, то прямая М0 М1 называется секущей. Будем перемещать М1 вдоль L так, чтобы
М1 стремилась к совпадению с М0 . Предельное положение секущей М0 М1 (если оно существует) при
М1 →М0 называется касательной к кривой L в точке М0.
Обозначим: 
Т.к. М1 →М0, 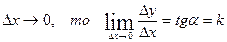 , где k – угловой коэффициент касательной.
, где k – угловой коэффициент касательной.
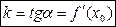
В этом и заключается геометрический смысл производной функции:
- производная  функции
функции 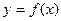 равна угловому коэффициенту касательной, проведённой к графику данной функции в точке с абсциссой
равна угловому коэффициенту касательной, проведённой к графику данной функции в точке с абсциссой 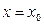 , а также тангенсу угла наклона касательной к оси абсцисс.
, а также тангенсу угла наклона касательной к оси абсцисс.
Уравнение касательной, проведенной к кривой, заданной графиком 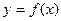 , в точке Мо(х0;у0) с конечным угловым коэффициентом
, в точке Мо(х0;у0) с конечным угловым коэффициентом 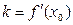 запишется так:
запишется так:
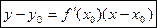
Из вышеизложенного видно, что наличие в точке графика функции 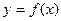 касательной, непараллельной оси ординат (т.к.
касательной, непараллельной оси ординат (т.к. 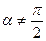 ), эквивалентно дифференцируемости функции в соответствующей точке.
), эквивалентно дифференцируемости функции в соответствующей точке.
Кроме касательной к графику функции в некоторой точке Мо(х0;у0), рассматривается и другая прямая, проходящая через эту точку. Прямая, перпендикулярная касательной к кривой и проходящая через точку касания, называется нормалью к кривой. Из определения нормали следует, что её угловой коэффициент связан с угловым коэффициентом касательной равенством, выражающим условие перпендикулярности двух прямых. Тогда уравнение нормали запишется так:
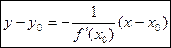
Если же 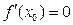 , то нормаль параллельна оси ординат.
, то нормаль параллельна оси ординат.
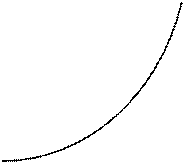 Пример1. Напишите уравнение касательной и нормали к линии
Пример1. Напишите уравнение касательной и нормали к линии 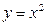 в точке
в точке 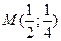
|
|
|


 В рассматриваемом примере
В рассматриваемом примере 
Найдем 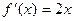
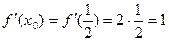
Подставим полученные значения в уравнения
касательной и нормали.
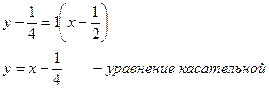
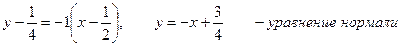
Пример2. Определите угол наклона касательной, проведенной к кривой  в точке с абсциссой
в точке с абсциссой 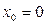
Т.к.  , то следует найти производную.
, то следует найти производную.
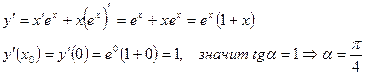
*Составьте уравнение касательной и нормали к графику 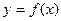 в точке
в точке 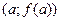
а) 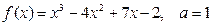
б) 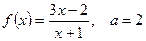
в) 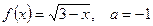
*Найдите углы, которые образуют касательные к кривым, проведенные в точке пересечения с осью абсцисс
а) 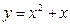
б) 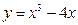
*В какой точке графика функции 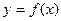 касательная наклонена к оси Ох под углом
касательная наклонена к оси Ох под углом 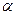 ?
?
а) 
б) 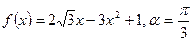
*Является ли прямая 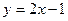 касательной к графику функции
касательной к графику функции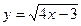
*Найдите точки, в которых касательная к графику функции 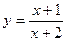 параллельна прямой
параллельна прямой 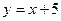
*Найдите уравнение прямой, проходящей через точку Р(0;2), касающейся графика функции 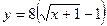 и пересекающей в двух различных точках параболу
и пересекающей в двух различных точках параболу 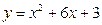
– Конец работы –
Эта тема принадлежит разделу:
Непрерывность функции. Точки разрыва. Асимптоты графика функции
Правила дифференцирования... Таблица производных основных функций...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Уравнение касательной и нормали к плоской кривой
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов