рефераты конспекты курсовые дипломные лекции шпоры

Раздел Компьютеры
/
Приближенные вычисления.

Реферат Курсовая Конспект

Выберите учебное заведение

Приближенные вычисления.

Приближенные вычисления. - раздел Компьютеры, Непрерывность функции. Точки разрыва. Асимптоты графика функции Формулу ...

Формулу 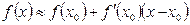используют для приближённого вычисления значений функций. Допускаемая при этом погрешность мала при малых значениях 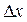, т.е. близких к 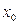. Применяя данную формулу легко получить различные формулы для нахождения приближенных числовых значений.

Приближенное вычисление степеней. Рассмотрим функцию 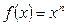. Пусть аргумент х получает малое приращение 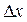.Вычислим приближенное значение функции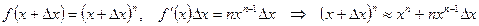

Пример1

Найти приближенное значение 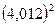. Полагая, что х = 4, =0,012, получим, 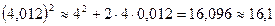(точный ответ 16,096144)

Приближенное вычисление корней. Рассмотрим функцию 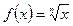. Пусть аргумент х получает малое приращение 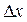.Вычислим приближенное значение функции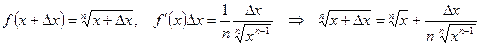

Пример2

Найти приближенное значение 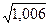. Полагая, что х = 1, =0,006, получим,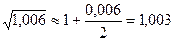

Приближенное вычисление синусов и тангенсов малых углов. Пусть для функции 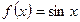аргумент х=0 получает малое приращение . Вычислим приближенное значение функции: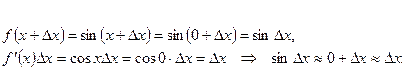

Синус малого угла приближенно равен самому углу (угол берется в радианной мере). Аналогичным образом можно показать, что имеет место приближение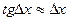

Пример3

Вычислить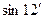

Т.к. 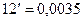рад, то sin0.0035=0.0035. По таблице натуральных значений синуса находим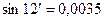

*Найдите приближенное значение степеней: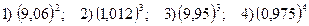

*Найдите приближенное значение корней: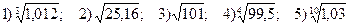

*Вычислите: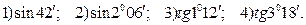

Развернуть

Открыть в широком формате

– Конец работы –

Эта тема принадлежит разделу:

Непрерывность функции. Точки разрыва. Асимптоты графика функции

Правила дифференцирования... Таблица производных основных функций...

Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Приближенные вычисления.

Что будем делать с полученным материалом:

Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:

Все темы данного раздела:

Непрерывность функции. Точки разрыва. Асимптоты графика функции

Уравнение касательной и нормали к плоской кривой
у1 у0

Эластичность функции
Будем рассматривать дифференцируемую функцию . Как и ранее,

Вычисление дифференциала функции
Дифференциалом функции у=f(x) называется произведение производной этой функции на произвольно

Применение производной к исследованию функции
Функция y=f(x) называется возрастающей в промежутке , ес

Интегральное исчисление. Неопределенный интеграл и его свойства
Будем считать, что мы достаточно хорошо освоили операцию дифференцирования одной переменной и, используя таблицу производных и основные правила дифференцирования, уверенно вычисляем производные осн

Основные свойства неопределенного интеграла
1° 2°

Несколько стандартных правил интегрирования
Правило подведения под знак дифференциала. Правило основано на следующем очевидном утверждении, которое следует из инвариантности фо

Определенный интеграл
Понятие определенного интеграла. Рассмотрим функцию

Дифференциальные уравнения
Некоторые понятия теории дифференциальных уравнений. Многие процессы экономики, физики, химии, астрономии, биологии описываются одной функцией у=у(х), заданной на некотором множеств

Дифференциальные уравнения I порядка
Простейшим дифференциальным уравнением I порядка называется дифференциальное уравнение вида

Линейное дифференциальное уравнение второго порядка с постоянными коэффициентами
До сих пор мы ограничивались рассмотрением дифференциальных уравнений первого порядка, т.е. таких уравнений, в которые искомая функция входит только под знаком первой производной. Но в приложениях

Теорема 2. Для того чтобы функция являлась решением уравнения (2), необходимо и достаточно, чтобы число являлось корнем уравнения
(4) Доказательство. Очевидно, что для указанной функ