рефераты конспекты курсовые дипломные лекции шпоры

Раздел Программирование
/
Линейная корреляция

Реферат Курсовая Конспект

Выберите учебное заведение

Линейная корреляция

Линейная корреляция - раздел Программирование, Курсовая работа по курсу "Вычислительная математика и программирование" по теме "Обработка экспериментальных данных" Предположим, Известно, Что Случайные Величины Х И Y Связаны Линейной Корреляц...

Предположим, известно, что случайные величины Х и Y связаны линейной корреляционной зависимостью (обе линии регрессии прямые). Требуется по опытным данным найти уравнения прямых линий регрессии Х на Y и Y на Х и оценить силу линейной корреляционной связи.

Рассмотрим сначала простейший случай, когда в результате независимых опытов была получена совокупность n пар чисел (x₁,y₁), (x₂,y₂), … , (x_n,y_n) (каждая пара чисел наблюдалась только по одному разу). Тогда искомое уравнение прямой линии регрессии Y на Х будет иметь вид:

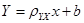(2.3)

где 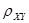- выборочный коэффициент регрессии Y на Х.

Уравнение (2.3) называют выборочным уравнением прямой линии регрессии Y на Х. Будем находить параметры 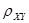и b уравнения (2.3), основываясь на методе наименьших квадратов, т.е. такими, чтобы сумма квадратов отклонений опытных значений y_i от значений 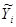(i=1,2, … , n), вычисленных по уравнению (2.3), была минимальной:

Метод наименьших квадратов описан в разделе 2.3.

Система нормальных уравнений для определения 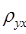и b имеет вид :

(2.4)

Решив эту систему, найдём искомые параметры:

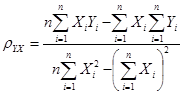	;	(2.5)
	.	(2.6)

Аналогично можно найти выборочное уравнение прямой линии регрессии X на Y:

Х=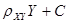

(2.7)

где 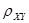- выборочный коэффициент регрессии Х на Y.

Для характеристики силы линейной корреляционной связи между величинами Х и Y по опытным данным находим выборочный коэффициент корреляции :

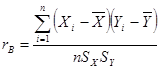(2.8)

где

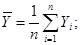
S_X, S_Y – выборочные средние квадратические отклонения:

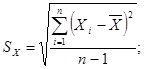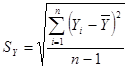(2.9)

Для практического использования более удобным являются формулы:

	;	(2.10)
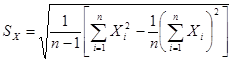	;	(2.11)
	.	(2.12)

Проверка значимости коэффициента корреляции изложена выше.

Пример 2.2. Термодинамические характеристики гидратации ионов в растворе – энтальпия и энтропия 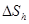для ряда ионов имеют значения, представленные в табл. 2.3 (Y=; Х=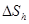). Найти зависимость энтальпии Y от энтропии Х и вычислить выборочный коэффициент корреляции.

Решение. Представим в табл.2.3, кроме исходных данных, результаты вычислений коэффициентов системы (2.4). Подставим из табл.2.3 вычисленные суммы в (2.5) и (2.6) найдём значения 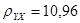и b = 260,58. Следовательно, искомое уравнение регрессии Y на Х будет иметь вид: Y=10,96Х + 260,58.

Выборочный коэффициент корреляции найдём по формуле (2.8), предварительно вычислив по формулам (2.10 –2.12):

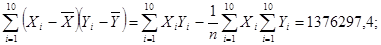
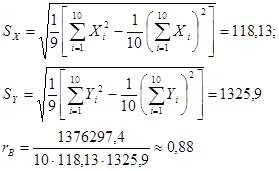
Коэффициент корреляции значимый, т.к. произведение H =½r½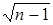= 0.88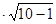= 2.64 больше табличного для уровня значимости 0.95 (H_табл=1.90).

Таблица 2.3

Исходные данные и результаты вычислений коэффициентов системы (2.4)

I	Ион	Х_i кДж /(моль ∙К)	Y_i кДж/моль
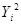
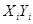
1	Ва²⁺	-134	-1329	17956	1766241	178086
2	Be²⁺	-239	-2516	57121	6330256	601324
3	Ca²⁺	-184	-1613	33856	2601769	296792
4	Co²⁺	-258	-2041	66564	4165681	526578
5	Cr³⁺	-422	-4618	178084	21325924	1948796
6	Fe³⁺	-418	-4476	174724	20034576	1870968
7	In³⁺	-394	-4194	155236	17589636	1652436
8	La³⁺	-364	-3328	132496	11075584	1211392
9	Pb²⁺	-130	-1516	16900	2298256	197080
10	Sr²⁺	-171	-1503	29241	2259009	257013
S	-2714	-27134

Таким образом, можно считать достаточно тесной линейную зависимость энтальпии и энтропии для любых ионов, т.к. это подтвердилось для десяти различных ионов.

По аналогии с примером 2.2 в курсовой работе необходимо исследовать наличие линейной связи между двумя физическими свойствами из приведенных в задании ко второй части курсовой работы (например, Х_i=ρ_i; Y_i=μ_iили Х_i=μ_i; Y_i=Ср_i).

Развернуть

Открыть в широком формате

– Конец работы –

Эта тема принадлежит разделу:

Курсовая работа по курсу "Вычислительная математика и программирование" по теме "Обработка экспериментальных данных"

ОДЕССКИЙ ГОСУДАРСТВЕННЫЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ... Химико технологический факультет...

Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Линейная корреляция

Что будем делать с полученным материалом:

Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:

Все темы данного раздела:

М Е Т О Д И Ч Е С К И Е У К А З А Н И Я
по выполнению курсовой работы по курсу "Вычислительная математика и программирование" по теме "Обработка экспериментальных данных" для

Одесса 1999
Методические указания по выполнению курсовой работы по курсу "Вычислительная математика и программирование" по теме "Обработка экспериментальных данных" для студентов 1 кур

СТРУКТУРА КУРСОВОЙ РАБОТЫ
Курсовая работа состоит из двух частей. При выполнении первой части курсовой работы по заданным экспериментальным данным необходимо: 1) провести корреляционный анализ и установить наличие

Теоретические сведения
Под корреляцией понимается всякая связь между двумя или несколькими исследуемыми явлениями. Она может быть детерминистической или случайной (вероятностной). Первый тип связи

Метод наименьших квадратов
Исследование и оптимизация сложных, плохо организованных систем возможны лишь с помощью статистических, вероятностных методов. Исходной точкой для таких исследований является аналог

Метод наименьших квадратов
Эмпирическая формула в общем виде может быть записана в следующем виде:

Требуется определить коэффициент эмпирической формулы
F(Xi,aj) = a + b∙Xi. (2.17) Тогда выражение (2.15) примет вид:

Анализ уравнения регрессии
Дисперсия адекватности модели Sад2 характеризует меру отклонения данных , пол

Представление экспериментальных данных формулами без использования МНК
Для расчетов и оптимизации, как правило, вместо табличных данных и графиков используются формулы, которые отражают закономерности табличного или графического материала. Когда теория процесса отсутс

Выбор эмпирической формулы. Метод выравнивания.
В некоторых случаях выбор типа эмпирической формулы может быть произведен на основе теоретических представлений о характере изучаемой зависимости. В других случаях приходится подбир

Метод выбранных точек
Пусть эмпирическая формула имеет вид (2.35) Требуется найти значение коэффициентов а и b. Наносим на координатную плоскость опытные точки (Xi,Yi). Как можно ближе к этим точкам проводим пр

Метод средних
Пусть эмпирическая формула имеет вид (2.35). Подставим в нее в место Х и Y опытные значения Xi и Yi. Так как левая часть формулы обычно не равна правой, получим систему уравне

Постановка задачи интерполирования
Пусть некоторая функция Y=f(Х) задана таблицей (табл. 3.1), т.е. при значениях аргумента X = X0, X1, ..., Xn функция f(Х)

Метод Лагранжа
Пусть при Х = Х0, Х1, Х2, ..., Хn функция f(X)принимает соответственно значения Y0, Y1, Y

Понятие о конечных разностях различных порядков
Для таблицы функцииY = f(X) с постоянным шагом h (т.е. с равноотстоящими узлами интерполяции): Xk

Первая интерполяционная формула Ньютона для равноотстоящих узлов интерполяции
Будем искать многочлен Рn(х) степени п, удовлетворяющий условиям (3.2), в виде

Вторая интерполяционная формула Ньютона для равноотстоящих узлов интерполяции
Получим формулу, которой удобно пользоваться для интерполирования (экстраполирования) функции у =f(х) в конце таблицы. Напишем искомый интерполяционный мног

Конечные разности
X y Dy D2y D3y 283,15 1,308

Обратное интерполирование
Пусть функция у = f(х) задана таблично. Задача обратного интерполирования заключается в том, чтобы по заданному значению функции