рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Программирование
- /
- Первая интерполяционная формула Ньютона для равноотстоящих узлов интерполяции
Реферат Курсовая Конспект
Первая интерполяционная формула Ньютона для равноотстоящих узлов интерполяции
Первая интерполяционная формула Ньютона для равноотстоящих узлов интерполяции - раздел Программирование, Курсовая работа по курсу "Вычислительная математика и программирование" по теме "Обработка экспериментальных данных" Будем Искать Многочлен РN(Х) Степ...
Будем искать многочлен Рn(х) степени п, удовлетворяющий условиям (3.2), в виде
| Рп(х)= a0 + a1 (x – x0) + a2 (x – x0) (x – x1) + a3 (x – x0) (x – x1) (x – x2) + … + an (x – x0) (x – x1) (x – x2) …(x – xn-1), | (3.15) |
где x0, x1, … xn — заданные значения аргумента х, причем xi — xi–1 = h = сопst (i=0,1, ... , n), коэффициенты a0, a1, .. , an нам неизвестны. Будем их определять, исходя из условий (3.2).
Положим в формуле (3.15) х =x0 . Тогда Рn(x0) = a0 . Однако, в силу условий (3.2), Рn(x0) = y0 . Следовательно, a0 = y0 .
Для определения a1полагаем в (3.15) х = х1, после чего получим
Рn(x1) = a0 + a1 (x1 – x0).
Учитывая, что Рn(x1) = y1 , a0 = y0 , (x1 – x0) = h , можем записать y1 = y0 + a1h, откуда 
. Однако y1 – y0 = Dy0 — конечная разность 1-го порядка, следовательно, 
.
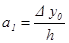Далее, полагая х = х2, получим
Рn(x2) = a0 + a1 (x2 – x0) + a2 (x2 – x0) (x2 – x1).
Так как Рn(x2) = y2 , a0 = y0 , 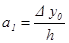, (x2 – x0) = 2h, (x1 – x0) = h , запишем:
y2 = y0 +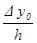 
2h + a22hh;
отсюда
a2 = 
.
Но Dy0 = y1 – y2, поэтому
y2 – y0 – 2Dy0 = y2 – y0 – 2 (y1 – y0) = y2 – 2 y1 + y0 =D2y0 .
Следовательно,
a2 = 
.
Аналогичные дальнейшие вычисления (с учетом формулы {3.14), выражающей разности различных порядков через значения функции), позволяют записать остальные коэффициенты:
a3 = 
,… ak = 
,… an = 
.
Подставив найденные выражения коэффициентов в формулу (3.15), получим
Рп(х) = y0 + 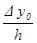(x – x0) + (x – x0) (x – x1) + (x – x0) (x – x1) (x – x2) + … +
+…+ (x – x0) (x – x1) (x – x2)… (x – xn–1). (3.16)
Это и есть первая интерполяционная формула Ньютона. Ее можно представить в несколько ином виде, более удобном для практического использования. Обозначим
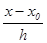= q.
Тогда
= q — 1;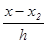 
= q — 2; …
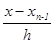= q – n + 1
и формула (3.16) приобретает вид
Рп(х) = y0 + qDy0 + 
D2y0 + 
D3y0 + … +
+…+  Dny0 .
| (3.17) |
Формулу (3.17) целесообразно использовать для интерполирования (экстраполирования) функции y=f(x) в окрестности начального значения x0, где qмало по абсолютной величине.
Если в формуле (3.17) принять п= 1, получим формулу линейного интерполирования:
Р1(х) = y0 + qDy0 .
При n = 2 будем иметь формулу параболического, или квадратичного, интерполирования:
Р2(х) = y0 + qDy0 + D2y0 .
При применении первой интерполяционной формулы Ньютона удобно пользоваться горизонтальной таблицей конечных разностей, так как тогда нужные значения разностей функции находятся в соответствующей горизонтальной строке таблицы.
Степень п многочлена Рn(х) на практике желательно выбирать так, чтобы конечные разности Dnyi были практически постоянными. За начальное значение x0 можно принимать любое табличное значение аргумента х.
– Конец работы –
Эта тема принадлежит разделу:
Курсовая работа по курсу "Вычислительная математика и программирование" по теме "Обработка экспериментальных данных"
ОДЕССКИЙ ГОСУДАРСТВЕННЫЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ... Химико технологический факультет...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Первая интерполяционная формула Ньютона для равноотстоящих узлов интерполяции
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?
Подпишитесь на Нашу рассылку
Реклама
Информация в виде рефератов, конспектов, лекций, курсовых и дипломных работ имеют своего автора, которому принадлежат права. Поэтому, прежде чем использовать какую либо информацию с этого сайта, убедитесь, что этим Вы не нарушаете чье либо право.
© copyright 1999 - 2024 allRefs.net. Все права защищены. Страница сгенерирована за: 0.018 сек.
Новости и инфо для студентов