рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Программирование
- /
- Анализ уравнения регрессии
Реферат Курсовая Конспект
Анализ уравнения регрессии
Анализ уравнения регрессии - раздел Программирование, Курсовая работа по курсу "Вычислительная математика и программирование" по теме "Обработка экспериментальных данных" Дисперсия Адекватности Модели SАд2 Хара...
Дисперсия адекватности модели Sад2 характеризует меру отклонения данных 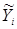 , полученных расчетом по уравнению регрессии (2.17) от реальных экспериментальных результатов yi для i-й точки, в которой проведено измерение. Значение Sад2 находят по формуле:
, полученных расчетом по уравнению регрессии (2.17) от реальных экспериментальных результатов yi для i-й точки, в которой проведено измерение. Значение Sад2 находят по формуле:
Sад2 = 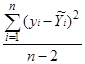 , ,
| (2.23) |
при числе степеней свободы f = n – 2.
После вычисления коэффициентов модели a и b вычисляют дисперсии Sa2 и Sb2,связанные с определением коэффициентов:
Sb2=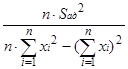 ; Sa2= ; Sa2=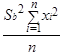 , ,
| (2.24) |
при числе степеней свободы f = n – 2.
После вычисления дисперсий следует проверить статистическую значимость a и b. Эта проверка дает ответ на вопросы о том, проходит ли прямая (2.13) через начало координат или нет, и отличается ли угол ее наклона от 450. Наиболее простым критерием значимости для такой проверки является критерий Стьюдента (t–.критерий). Величина критерия Стьюдента зависит от уровня доверительности Р и числа степеней свободы f , т.е. t = t(Р, f). Часто вместо уровня доверительности пользуются понятием уровень значимости α = 1– Р .
Значения критерия Стьюдента для Р = 0.95приведены в табл.2.4.
Таблица 2.4
Значения критерия Стьюдента для уровня доверительности Р = 0.95
| n-k | |||||||||
| t | 12.7 | 4.30 | 2.80 | 2.45 | 2.30 | 2.23 | 2.03 | 2.09 | 2.04 |
где n – число опытов, k – число определяемых из них констант
Доверительные границы 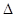 a и
a и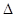 b для этих коэффициентов вычисляются по формулам:
b для этих коэффициентов вычисляются по формулам:
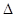 a= a= tα/2,f ∙sa ; tα/2,f ∙sa ; 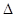 b= b= tα/2,f ∙sb tα/2,f ∙sb
| (2.25) |
Коэффициенты уравнения значимы, если выполняются условия a>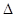 a и b>
a и b>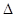 b.
b.
После определения коэффициентов регрессии и оценки их значимости проверяют адекватность самого уравнения регрессии. Отклонение расчетного значения 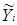 от экспериментального yi может иметь место либо потому, что избранная модель несовершенна, либо вследствие случайных погрешностей. Поэтому статистическая оценка адекватности производится по F–критерию:
от экспериментального yi может иметь место либо потому, что избранная модель несовершенна, либо вследствие случайных погрешностей. Поэтому статистическая оценка адекватности производится по F–критерию:
| Fэксп=Sад2/Sy2 | (2.2) |
при числе степеней свободы числителя n–2, а знаменателя n(m –1). Здесь  Sy2 –дисперсия воспроизводимости при измерении величины y или выборочная дисперсия.
Sy2 –дисперсия воспроизводимости при измерении величины y или выборочная дисперсия.
Значения критерия Фишера для уровня доверительности Р = 0.95приведены в табл.2.5.
Таблица 2.5
Значения критерия Фишера для уровня доверительности Р = 0.95
| m–1 (m-k) | F–критерий при разных n-k | |||||||
| 18.50 | 19.00 | 19.25 | 19.33 | 19.37 | 19.39 | 19.43 | 19.47 | |
| 10.13 | 9.55 | 9.12 | 8.94 | 8.84 | 8.78 | 8.69 | 8.60 | |
| 7.71 | 6.94 | 6.39 | 6.16 | 6.04 | 5.96 | 5.84 | 5.71 | |
| 6.61 | 5.79 | 5.19 | 4.95 | 4.82 | 4.74 | 4.60 | 4.46 | |
| 5.99 | 5.14 | 4.53 | 4.28 | 4.15 | 4.06 | 3.92 | 3.77 | |
| 5.32 | 4.46 | 3.84 | 3.58 | 3.44 | 3.34 | 3.20 | 3.06 |
где m – число параллельных опытов
Выборочная дисперсия Sy2 определяется при обработке результатов параллельных измерений yi в каждой точке по формуле:
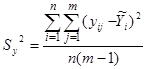 .
.
Eсли значение Fэксп , полученное по формуле (2.26), меньше табличного при избранном уровне значимости, то уравнение (2.3) адекватно описывает экспериментальные результаты. Если Fэксп. Fтабл, следует предложить другой вид уравнения и исследовать новое уравнение регрессии.
Fтабл, следует предложить другой вид уравнения и исследовать новое уравнение регрессии.
Пример2.3. Зависимость давления насыщенного пара бензола от температуры выражается следующими экспериментальными данными (табл. 2.6)
Таблица 2.6
Давление насыщенного пара бензола при разных температурах
| T, K | 270.5 | 280.8 | 288.6 | 299.2 | 315.4 | 333.8 | 353.2 |
| P×10—5, Па | 0.0267 | 0.0533 | 0.080 | 0.1333 | 0.2667 | 0.5333 | 1.0133 |
Для этой зависимости определить коэффициенты уравнений линейной регрессии
| Р = b + a × T | (2.27) |
и нелинейной регрессии вида
| Р = b × exp (a/T) | (2.28) |
Произвести анализ адекватности обеих моделей
Для линейной регрессии (Y = a + b × X) определяем коэффициенты нормальных уравнений.
Для этого проводим предварительные вычисления (см. табл. 2.7).
Система нормальных уравнений имеет вид:
| 7 × а + 2.141×10 3× b = 2.106×10 5 2.141×10 3 × а + 6.609×10 5 × b = 7.052×10 7 | (2.29) |
Решив систему (2.29) находим значения коэффициентов
a = – 2.806 × 105
b = 1016
Линейная регрессия имеет вид:
| P = – 2.806 × 105 + 1016 T, | (2.30) |
где Р – давление, Па; Т – температура, К.
Таблица 2.7
Данные для расчета коэффициентов нормальных уравнений
| I | X = T | Y = P | X×Y | X2 |
| 1 | 270.5 | 2670 | 722200 | 73170 |
| 2 | 280.8 | 5330 | 1496700 | 78849 |
| 3 | 288.6 | 8000 | 2308800 | 83290 |
| 4 | 299.2 | 13330 | 3988300 | 89521 |
| 5 | 315.4 | 26670 | 8411700 | 99477 |
| 6 | 333.8 | 53330 | 17801500 | 111422 |
| 7 | 353.2 | 101330 | 35789700 | 125174 |
| S | 2141.5 | 2.106×105 | 7.052×107 | 6.609×105 |
Рассчитываем по уравнению (2.30) давление пара в каждой точке (табл. 2.8).
Таблица 2.8
Расчетное давление пара (по уравнению (2.30))
| I | X = T | Y = P | 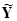
| Y–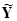
| (Y–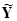 )2 )2
|
| 1 | 270.5 | 2670 | –5800 | 8470 | 71.74×106 |
| 2 | 280.8 | 5330 | 4700 | 630 | 0.040×106 |
| 3 | 288.6 | 8000 | 12600 | –4600 | 21.16×106 |
| 4 | 299.2 | 13330 | 23400 | –10070 | 101.40×106 |
| 5 | 315.4 | 26670 | 39800 | –13130 | 172.40×106 |
| 6 | 333.8 | 53330 | 58500 | –5170 | 26.73×106 |
| 7 | 353.2 | 101330 | 78200 | –23130 | 535.00×106 |
| S | 928.43×106 |
Дисперсия адекватности модели (по формуле 2.23)
Sад = (928.43×106)/(7–2) = 185 ×106
Выборочную дисперсию Sy2 определяем по точности измерения давления dy = ± 2% и, следовательно, по среднему отклонению
Dy = ± 0.02×Y ср = ± 0.02×SYi / 7 = ± 0.02× 210660 / 7 = ± 602 Па
При минимальном количестве параллельных измерений в каждой точке m = 2 дисперсия воспроизводимости составит:
Sy2=  = 0.725∙106
= 0.725∙106
Критерий Фишера по формуле (2.26)

Табличное значение критерия Фишера (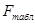 ) находим по числу степеней свободы числителя (
) находим по числу степеней свободы числителя (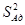 ) и знаменателя (
) и знаменателя (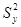 )
)
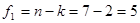
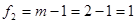 ,
,
где 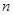 = 7, количество экспериментальных точек ;
= 7, количество экспериментальных точек ;
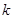 = 2, количество найденных коэффициентов модели ;
= 2, количество найденных коэффициентов модели ;
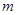 = 2, количество параллельных измерений в каждой точке, принимаем минимальное значение
= 2, количество параллельных измерений в каждой точке, принимаем минимальное значение 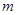 = 2.
= 2.
По табл.2.5 F5,1 = 229.5.
Так как Fэкс > Fтабл,, то линейная модель неадекватна результатам эксперимента. Это видно и по величинам вычисленных значений 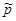 , которые значительно отличаются от экспериментальных.
, которые значительно отличаются от экспериментальных.
При выполнении курсовой работы возможны варианты адекватности линейной модели.
Рассмотрим теперь уравнение нелинейной регрессии. Заданную нелинейную зависимость (2.28) необходимо предварительно привести к линейному виду. Логарифмируя формулу (2.28), получим:
| lg P = lg b + a×lg e/T | (2.31) |
Обозначив Y= lgP; a0 = lgb; a1= a×lge; X= 1/T, получим следующую линейную зависимость:
| Y = a0 + a1×X | (2.32) |
Вычисленные значения Y= lgP; X= 1/T приведены в табл. 2.9.
Таблица 2.9
Определение коэффициентов системы нормальных уравнений
| I | X = 1/T | Y = lgP | X2 | X×Y |
| 0.003697 | -1.5735 | 1.367×10-5 | -5.817×10-3 | |
| 0.003561 | -1.2733 | 1.268×10-5 | -4.534×10-3 | |
| 0.003465 | -1.0969 | 1.201×10-5 | -3.801×10-3 | |
| 0.003342 | -0.8752 | 1.117×10-5 | -2.925×10-3 | |
| 0.003171 | -0.5740 | 1.006×10-5 | -1.820×10-3 | |
| 0.002952 | -0.2730 | 0.8714×10-5 | -0.806×10-3 | |
| 0.002831 | 0.005738 | 0.8015×10-5 | 0.01624×10-3 | |
| S | 0.02302 | -5.6602 | 7.632×10-5 | -0.01969 |
Система нормальных уравнений имеет вид:
| 7×a0 + 0.02303×a1= -5.6602 | (2.33) | |
| 0.02303×a0 + 0.7632×10-4×a1 = -0.01969 |
Решив систему (2.33), находим значение коэффициентов a0 = 4.998 и a1 = -1767.4.
Поскольку, в силу введенных нами обозначений a0 = lgb, то b = 99471.8; a1= a×lge, то a =lgа = –1767.4/0.4343= -4069.5.
Тогда искомая зависимость примет вид:
| p = 99471.8×e-4069.5/T | (2.34) |
где р – давление насыщенного пара, бар (1 бар = 105Па).
Рассчитываем по уравнению (2.34) давление пара в каждой точке (табл. 2.10).
Адекватность модели проверяем аналогично предыдущему варианту.
Дисперсия адекватности модели (по формуле 2.23)
Sад = (6.2476×10-3)/(7–2) = 1.2495 ×10-3
Среднее отклонение при измерении давления (в барах) составит:
∆y = ± 602×10-5 = ± 6.02×10-3 бар
Выборочная дисперсия воспроизводимости
Sy2 = 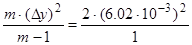 =7.248×10-5
=7.248×10-5
Критерий Фишера по формуле (2.26)
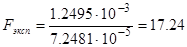
Таблица 2.10
Расчетное давление пара (по уравнению (2.34))
| I | X = T, K | Y = P, бар | 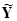
| Y–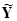
| (Y–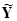 )2 )2
|
| 1 | 270.5 | 0.0267 | 0.0291 | –0.0024 | 0.00576×10-3 |
| 2 | 280.8 | 0.0533 | 0.0505 | 0.0028 | 0.00784×10-3 |
| 3 | 288.6 | 0.0800 | 0.0748 | 0.0052 | 0.0270×10-3 |
| 4 | 299.2 | 0.1333 | 0.1233 | 0.010 | 0.100×10-3 |
| 5 | 315.4 | 0.2667 | 0.2477 | 0.0190 | 0.361×10-3 |
| 6 | 333.8 | 0.5333 | 0.6039 | –0.0706 | 4.984×10-3 |
| 7 | 353.2 | 1.0133 | 0.9857 | 0.0276 | 0.762×10-3 |
| S | 6.2476×10-3 |
Табличное значение критерия Фишера (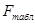 ) остается такое же F5,1 = 229.5.
) остается такое же F5,1 = 229.5.
В данном случае Fэкс < Fтабл,, поэтому исследуемая нелинейная модель может быть принята как адекватная.
При выполнении курсовой работы возможен вариант неадекватности и нелинейной модели.
– Конец работы –
Эта тема принадлежит разделу:
Курсовая работа по курсу "Вычислительная математика и программирование" по теме "Обработка экспериментальных данных"
ОДЕССКИЙ ГОСУДАРСТВЕННЫЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ... Химико технологический факультет...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Анализ уравнения регрессии
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов