рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Математика
- /
- Случайные события.
Реферат Курсовая Конспект
Случайные события.
Случайные события. - раздел Математика, Предмет теории вероятностей Случайный Опыт – Это Создание Заданного Комплекса Условий И ...
Случайный опыт – это создание заданного комплекса условий и наблюдение результата. Результат интерпретируется как случайное событие(исход).
Пространство элементарных исходов – мн-во простейших(неразложимых в рамках данного опыта на более простые) взаимоисключающих исходов  так, что опыт всегда заканчивается появлением одного и только одного элементарного исхода
так, что опыт всегда заканчивается появлением одного и только одного элементарного исхода 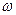 .
.
Случайное событие – любое подмн-во  пр-ва элем. исходов заданного случайного опыта. Если результат опыта
пр-ва элем. исходов заданного случайного опыта. Если результат опыта  , то событие А произошло.
, то событие А произошло.
Основные понятия связанные со случайными событиями:
1) Всё пр-во элементарных исходов в 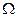 называется достоверным событием. Очевидно достоверное событие происходит в любом опыте.
называется достоверным событием. Очевидно достоверное событие происходит в любом опыте.
2) Пустое множество Ǿ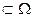 называется невозможным событием. Очевидно невозможное событие не происходит в опыте.
называется невозможным событием. Очевидно невозможное событие не происходит в опыте.
3) Суммой событий А и В называется событие А+В состоящее из элем исходов входящих в мн-во  . Т.о. событие А+В состоит в том что произошло хотябы одно из событий А и В.
. Т.о. событие А+В состоит в том что произошло хотябы одно из событий А и В.
4) Произведение А и В это событие сост. из элементарных исходов входящих в мн-во  . Т.о. произведение А и В состоит в том что А и В произошли одновременно.
. Т.о. произведение А и В состоит в том что А и В произошли одновременно.
5) Разность событий А и В – событие состоящее из элементарных исходов, входящих в мн-во АВ. Т.о. событие А произошло, а В нет.
6) Событие А влечет за собой В, если А – подмножество В(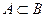 ). Т.о. всякий раз, когда происходит А, происходит и В.
). Т.о. всякий раз, когда происходит А, происходит и В.
7) Событие 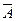 состоит из
состоит из  , не входящих в А, называется противоположным А
, не входящих в А, называется противоположным А
8) События А и В называются несовместными если нет  входяих в А и в В одновременно.
входяих в А и в В одновременно.
Св-ва:
1)Коммутативность:
А+В=В+А; АВ=ВА.
2)Ассоциативность:
(А+В)+С=А+(В+С); (АВ)С=А(ВС).
3)Дистрибутивность:
(А+В)С=АС+ВС; А+ВС=(А+В)(А+С).
№3 Классическое определение вероятности.
События равновероятные, если нет объективных оснований для того, чтобы, одно из них было более или менее вероятным чем другое.
Случайный опыт удовлетворяющий условиям:
а) 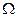 конечно.
конечно.
б) все элем. исходы равновозможны
называется классической схемой.
Пусть 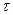 классическая схема,
классическая схема, 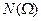 -число элементарных исходов,
-число элементарных исходов, 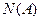 - число исходов благоприятствующих событию А. Тогда вероятность события А:
- число исходов благоприятствующих событию А. Тогда вероятность события А:
Р(А)= 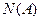 /
/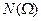 - формула классической вероятности.
- формула классической вероятности.
Св-ва:
1)Р(А)>0
2) 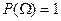
3)Если А и В несовместны, (АВ= Ǿ), то Р(А+В)=Р(А)+Р(В).
№4 Геометрические вероятности
Пусть случайный опыт состоит в случайном выборе точки на прямой R1 или плоскости R2 или n мерного пространства Rn.
На прямой рассмотрим только мн-ва 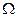 имеющие длину, на плоскости площадь, в R3-объем, в Rn- обобщенный объем.
имеющие длину, на плоскости площадь, в R3-объем, в Rn- обобщенный объем.
Длина, площадь, объем – мера множества 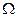 .
.
Пусть случайная точка  пропорциональна мере А (mes A) и не зависит от других обстоятельств. Такой случайный опыт называется геометрической схемой.
пропорциональна мере А (mes A) и не зависит от других обстоятельств. Такой случайный опыт называется геометрической схемой.
Пусть 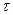 геометрическая схема, событие
геометрическая схема, событие  -измеримое мн-во. Тогда вероятностью события А называется число P(A)=mes(A)/mes(
-измеримое мн-во. Тогда вероятностью события А называется число P(A)=mes(A)/mes(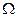 )
)
П1. 2 судна должны подойти к причалу для разгрузки в течении суток. Одновременная разгрузка невозможна. Разгрузка любого из них длится 8 часов. С какиой вероятностью одно будет ожидать разгрузки другого?
х- время прихода однеого
|
 у – время прихода другого
у – время прихода другого
(х,у) 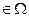 в R2
в R2
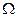 ={(х,у)
={(х,у) 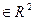 |
| 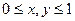 }
}
A = {(х,у) 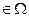 | |x-y|
| |x-y| 1/3}
1/3}
mes(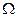 )=1, mes(A)=5/9;
)=1, mes(A)=5/9;
P(A)=5/9
Cв-ва:
1)Р(А) 
2) 
3)А и В несовместимы.
№5 Понятие об аксиоматической вероятности
Пусть  событию А, связанному со случайным опытом
событию А, связанному со случайным опытом 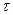 сопоставлена P(A). Это означает, что на мн-ве всех событий F определена числовая функция P(A),
сопоставлена P(A). Это означает, что на мн-ве всех событий F определена числовая функция P(A),  .
.
Чтобы вместе с вероятностью событий А и  можно было найти А+В, АВ, А-В,
можно было найти А+В, АВ, А-В, 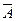 ,
, 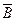 ,
, 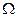 , Ǿ, нужно чтобы эти события входили в F, т.е. чтобы F было алгеброй событий.
, Ǿ, нужно чтобы эти события входили в F, т.е. чтобы F было алгеброй событий.
Если 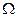 конечное или счетное мн-во, то алгеброй событий F будет мн-во всех подмн-в в
конечное или счетное мн-во, то алгеброй событий F будет мн-во всех подмн-в в 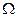 .
.
П1. А={ из 4х карточек 1,2,3 и 4 случайно выбирают одну}
Найдем F:
Ǿ

Пусть 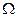 - множество элем. исходов, F – алгебра событий. Числова функция Р(А), определенная на F, называется вероятностью, если она подчиняется аксиомам:
- множество элем. исходов, F – алгебра событий. Числова функция Р(А), определенная на F, называется вероятностью, если она подчиняется аксиомам:
1) Р(А)  ,
,  (аксиома неотрицательности)
(аксиома неотрицательности)
2) 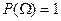 (аксиома нормировки)
(аксиома нормировки)
3) Для  и В
и В  , таких что АВ= Ǿ. Р(А+В)=Р(А)+Р(В) (аксиома сложения)
, таких что АВ= Ǿ. Р(А+В)=Р(А)+Р(В) (аксиома сложения)
1)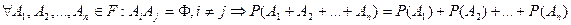
2)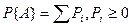 - вероятность элементарного исхода
- вероятность элементарного исхода
В П1 Р 
№6 Св-ва вероятности
Из основных св-в вероятности:
1) Р(А) 
2)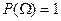
3)АВ= Ǿ => Р(А+В)=Р(А)+Р(В)
Вытекают другие св-ва:
4) 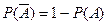
5) Р(Ǿ)=0
6) 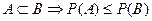
7) 
8)Р(А+В)=Р(А)+Р(В)-Р(АВ)
№7 Условная вероятность и ее свойства. Теорема умножения.
Пусть в случайном опыте Т могут появиться события А и В. Если известно что В произошло то говорят об условной вероятности события А при условии В Р(А/В).
В произошло => реализуется один из N(B) элементарных исходов  . Из N(AB) исходов
. Из N(AB) исходов 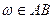 благоприятствуют A
благоприятствуют A
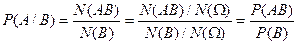
Опр. Пусть (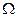 ,F,P) – вер. пространства , А,
,F,P) – вер. пространства , А,  и
и 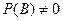 , тогда усл.вероятностью А наз-тся число :
, тогда усл.вероятностью А наз-тся число :

Замеч. 1)Аналогично , если  :
: 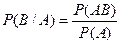
2) Теорема умноженияВер-ть произведения  событий равна вер-ти одного из них и умноженной на усл.вер-ть другой.
событий равна вер-ти одного из них и умноженной на усл.вер-ть другой.
1. 
2. 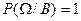
3. 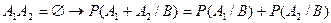

4)Усл вер-ть обладает всеми св-ми дрю вер-тей.
5) Усл. Вер-ть P(A/B) можно рассм.,как обычную вероятность, определенную на новом про-ве Эл. Исходов 
6) Для n событий формула :  обобщаеться
обобщаеться 
№8 Независимые события, их свойства. Независимость в совокупности.
Опр. А независимое событие от В , если P(A/B)=P(A)
Свойства:
1) Свойство независимости взаимно, т.е. P(B/A)=P(B)
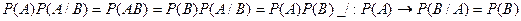
Т.е. А и В взаимно независимы.
2) Если А и В независимы , то P(AB)=P(A)*P(B) верно и обратное:
Опр. События А1,A2,A3,…,An независимы в совокупности , если любое из них не зависит от каждого из остальных n от всех возможных произведений этих остальных.
Опр. События A1,A2,…,An независимы в совокупности если : P(A1,A2,…,An)=P(A1)*P(A2)…P(An)
Замечание Для независимости в совокупности недостаточно попарной независимости.
№9 Формула полной вероятности.
Пусть события H1,…,Hn могут произойти в случайном опыте Т. Эти события образуют полную группу событийб если H1+H2+…+Hn=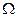
Если к томуже события {Hz} попарно несовместимы (Hi,Hj 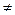 0, i
0, i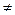 j), то они образуют полную группу несовместимых событий , т.е. в каждом опыте происходит одно и только одно из этих событий.
j), то они образуют полную группу несовместимых событий , т.е. в каждом опыте происходит одно и только одно из этих событий.
Теорема.
Пусть в случ опыте могут произойти события А,H1,..,Hn, причем {Hi} образуют полную группу несовместимых событий , то 
A=A*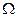 =A(H1+…+Hn)=AH1+…+AHn
=A(H1+…+Hn)=AH1+…+AHn
P(A)=P(AH1)+P(AH2)+…+P(AHn)=> теоре. Умножения
P(A)=P(H1)P(A/H1)+…+P(Hn)P(A/Hn)
№10 Формула Байеса
Теорема В условиях предыдущей теоремы
P(Hk/A)=(P(Hk)P(A/Hk))/P(A)
По теореме умножения P(A)*P(Hk/A)=P(A*Hk)=P(Hk)P(A/Hk) /: P(A)
P(Hk/A)=(P(Hk)P(A/Hk)/P(A))
№11 Схема Бернулли
Повторные испытания – это проведение n раз одного и тогоже случ опыта или проведение одновременное n одинаковых опытов.
Схема Бернулли – это случ опыт состоящий в n повторных испытаниях, причем
1) z исхода (А-успех, (не)А – неудача)
2) испытания независимы , т.е. P(A) не зависит от исходов в др. испытыниях
3) p и q=1-p не изм от пыта к опыту
Найдем вер-ть pn,m появления ровно m раз успеха в серии из т испытаний.
В силу независимости испытаний вер-ть каждого такого исхода равно  Число таких элементарных исходов
Число таких элементарных исходов 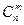 Потому :
Потому :
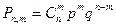
– Конец работы –
Эта тема принадлежит разделу:
Предмет теории вероятностей
На сайте allrefs.net читайте: "Предмет теории вероятностей"
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Случайные события.
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов