рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Математика
- /
- Дисперсия
Реферат Курсовая Конспект
Дисперсия
Дисперсия - раздел Математика, Предмет теории вероятностей D[X]= ...
D[x]= 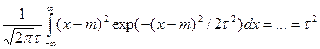
Найдем для x~N(m, 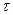 ) P{a<x<b}
) P{a<x<b}
P{a<x<b}=
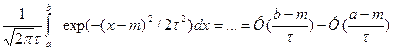
В частном случае P{/X-m/<l}=2Ф(l/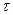 )-1
)-1
18. Случайный вектор. Функции совместного распределения вероятностей, её свойства.



19. Дискретный случайный вектор. Связь закона распределения двумерного случайного вектора с законами распределения его компонент. Независимость случайных величин. Условные законы распределения.


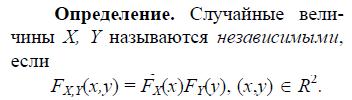

21. Математическое ожидание дискретной случайной величины, его свойства.

22. Начальные и центральные моменты
Опр. Начальным моментом k-ого порядка X называется число
αk[X]=M[X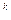 ]
]
1) α1[X]=M[X]
2) X – СВДТ => αk[X]=∑ X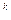 p
p
Опр. Центр. моментом k-ого порядка X называется число
μk[X]=M[(X-M[X])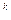 ]
]
1) Сл.величина X-M[X]=X (с точкой сверху) наз-ся центрир. случ. величиной.
2) μ1[X]=0
Связь между αk[X] и μk[X].
μk=M[(X-M[X])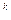 ]= M[
]= M[ X
X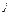 (-1)
(-1)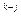 (M[X])
(M[X])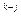 ]=
]=
=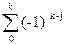
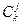 M[X
M[X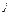 ](M[X])
](M[X])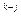
=> μk[X] = 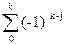
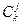 αj[X] * α
αj[X] * α [X]
[X]
23. Дисперсия случайной величины
Опр. Дисперсией случ.величины X назыв. ее второй центральный момент μ2[X]:
D[X] = M[(X-M[X]) ]
]
Для X – СВДТ: D[X] =  pi
pi
D[X] характеризует степень рассеяния, разбросанности значений X вокруг M[X].
Опр. Среднеквадратическим отклонением X назыв. число T[X] = 
Свойства:
1. D[X] больше, либо равно 0
2. D[C] = 0, C=const
3. D[X] = M[X ]-M
]-M [X]
[X]
4.D[cX] = c D[X]
D[X]
5.Если X и Y независимы, то D[X+Y] = D[X]+D[Y]
D[X+Y] = M[(X+Y-M[X+Y])  ] = M[(X-M[X]+Y-M[Y])
] = M[(X-M[X]+Y-M[Y]) ] =
] =
= M[(X-M[X])  ]+M[(Y-M[Y])
]+M[(Y-M[Y])  ] + 2M[(X-M[X])]*M[(Y-M[Y])] =
] + 2M[(X-M[X])]*M[(Y-M[Y])] =
= D[X] + D[Y] | M1=0 | | M1=0 |
24. Мат.ожидание и дисперсия СВНТ
Опр. Пусть X – СВНТ с функцией плотности fx(x), причем  fx(x)dx сходится абсолютно, тогда мат. Ожиданием X называется число M[X] =
fx(x)dx сходится абсолютно, тогда мат. Ожиданием X называется число M[X] =  fx(x)dx
fx(x)dx
Опр. Пусть X – СВНТ с функцией плотности fx(x), причем  fx(x)dx сходится абсолютно, тогда дисперсией X называется число: D[X] =
fx(x)dx сходится абсолютно, тогда дисперсией X называется число: D[X] = fx(x)dx
fx(x)dx
Замечание.
1)M[X] для X – СВНТ обладает теми же свойствами, что и для X-СВДТ
2)Опр-е нач. и центр. моментов сохр. на случай непр. случ. величины. Их свойства зависят от свойств M[X].
П1. X~N(m,τ);M[X] - ?
M[X] = 
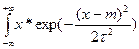 dx=…= m = M[X]
dx=…= m = M[X]
П2. X~N(m,τ);D[X] - ?
D[X] = = 
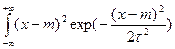 dx=… =
dx=… = 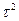
25. Функция случайной величины.





26. Характеристики распределения случайной величины: мода, медиана, квантили, коэффициенты асимметрии и эксцесса.






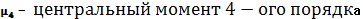
27. Характеристическая функция случайной величины, её свойства.


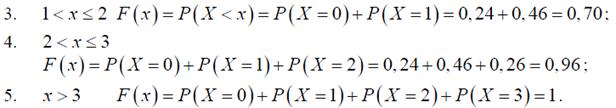
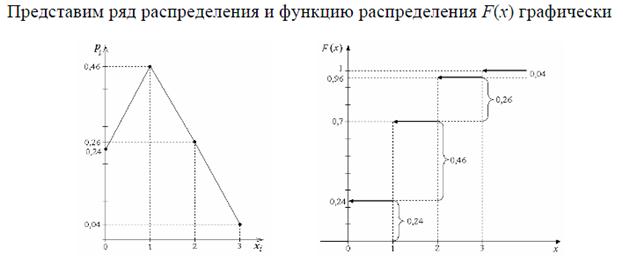
28. Характеристические функции биноминального, пуассоновского и нормального распределений вероятности.
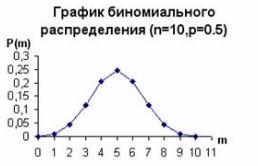
Биномиальное распределение в теории вероятностей — распределение количества «успехов» в последовательности из n независимых случайных экспериментов, таких что вероятность «успеха» в каждом из них равна p.

| 
|
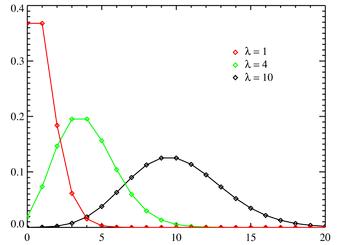
Распределение Пуассона моделирует случайную величину, представляющую собой число событий, произошедших за фиксированное время, при условии, что данные события происходят с некоторой фиксированной средней интенсивностью и независимо друг от друга. Распределение Пуассона играет ключевую роль в Теории массового обслуживания.

| 
|
Нормальное распределение, также называемое распределением Гаусса, — распределение вероятностей, которое играет важнейшую роль во многих областях знаний

| 
|
№29 Композиционая устойчивость
Опр.: Пусть X1 и Х2 распределены по одному и тому же закону (возможно с разными параметрами) и независимы. Если при этом Х1+Х2 распределена по тому же закону, то говорят, что данный закон композиционно устойчив.
П1:  ,
,  и Х1,Х2 независимы
и Х1,Х2 независимы
•  ,
, 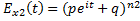 . Т.к. Х1 и Х2 независимы:
. Т.к. Х1 и Х2 независимы:  =>
=> 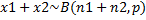 •
•
Т.е. при фиксированном значении p з-н B(n,p) композиционно устойчив.
П2:  ,
, 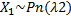
• 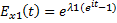 ,
, 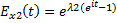 . Т.к. Х1 и Х2 независимы:
. Т.к. Х1 и Х2 независимы: 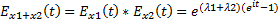 =>
=> 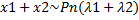 •
•
П3: 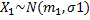 ,
, 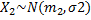 и Х1,Х2 независимы
и Х1,Х2 независимы
• 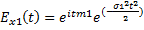 ,
, 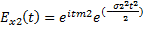
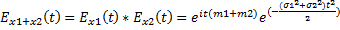 =>
=> 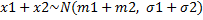 •
•
№30 Ковариация двух случайных величин:
Опр: Ковариацией Х и Y называется число (если  ):
):
сov[X,Y] = M[(X-M[X])(Y-M[Y])]= M[Ẋ,Ẏ].
Св-ва:
1) сov[X,Y] = сov[Y,X]
2) сov[X,X] = D[X]
3) сov[X,Y1+Y2] = сov[X,Y1] + сov[X,Y2]
4) сov[C*X,Y]= C* сov[X,Y]
5) D[X+Y]=D[X] + D[Y] + 2 сov[X,Y]
6) |сov[X,Y]| ≤ 
• 0≤ D[tX+Y] = t^2*D[X] + D[Y] + 2t*cov[X,Y]
 = 4 (сov[X,Y])^2 – 4* D[X]*D[Y] => |сov[X,Y]| ≤
= 4 (сov[X,Y])^2 – 4* D[X]*D[Y] => |сov[X,Y]| ≤  •
•
№31 Коэффициент корреляциии.
Опр: Коэффициентом корреляции называется число:
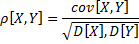
Св-ва:
1) 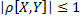
2) Если X и Y независимы => 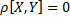 (обратное неверно)
(обратное неверно)
•cov[X,Y]=M[XY] – M[X]M[Y] = |тк Х и Y независимы|= M[X]M[Y] – M[X]M[Y] =0 =>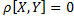 •
•
3) Если Y=aX+b, то 
• Пусть M[X] = m , D[X]=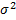 тогда M[Y] = am+b , D[Y]=
тогда M[Y] = am+b , D[Y]=
cov[X,Y] = M[(X-m)(ax+b – (am+b))] = a* M[(X-m)^2] = 
 •
•
Замеч: Если X и Y независимы, то 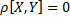 . Если Х и Y лин. зависимы
. Если Х и Y лин. зависимы  . Поэтому
. Поэтому  используется в качестве меры линейной зависимости Х и Y. Если
используется в качестве меры линейной зависимости Х и Y. Если 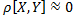 – зависимость слабая. Если
– зависимость слабая. Если 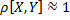 - зависимость сильная. Если
- зависимость сильная. Если  - то при росте одной случайной величины, другая в среднем растет.
- то при росте одной случайной величины, другая в среднем растет.
№32 Распределения 
Опр: Пусть Xi – независимые случайные величины,  . Тогда случайная величина
. Тогда случайная величина  имеет распределение
имеет распределение 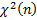 ( «хи-квадрат») с n степенями свободы -
( «хи-квадрат») с n степенями свободы - 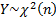
Св-ва:
1) M[Y]=n ; D[Y]=2n
2) Рисуем графики (оси: f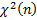 (x) и ось «х»)...n2>n1 хотя n2 более пологий и лежит ниже n1
(x) и ось «х»)...n2>n1 хотя n2 более пологий и лежит ниже n1
Опр: Пусть случ. величины  и
и 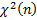 независимы. Тогда случ. величина Y распределена по закону Стьюдента:
независимы. Тогда случ. величина Y распределена по закону Стьюдента: 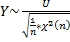 с n степенями свободы.
с n степенями свободы.  .
.
1) Рисуем графики (оси: St (x) и ось «х»)...n1>n2 - n2 более пологий и лежит ниже n1
(x) и ось «х»)...n1>n2 - n2 более пологий и лежит ниже n1
2) При 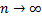 St(0,1) приближается к N(0,1)
St(0,1) приближается к N(0,1)
Опр: Пусть  и
и  - независимые случайные величины. Тогда
- независимые случайные величины. Тогда 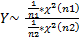 распределена по закону Фишера со степенями свободы n1 и n2
распределена по закону Фишера со степенями свободы n1 и n2
Св-во: Пусть Fn1,n2,p – квантиль распределения F(n1,n2) порядка p, тогда Fn1,n2,(1-p) = 1/ Fn1,n2,p
№33 Неравенства Чебышева
Теорема 1 ( 1ое неравенство Чебышева) :
Пусть Х – случайная величина,  . Тогда
. Тогда 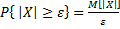
• Рассмотрим случайную величину 
Очевидно,  или
или 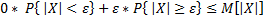 ;
;
 •
•
Теорема 2 (2ое неравенство Чебышева):
Пусть Х-случайная величина, 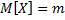 ,
, 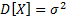 . Тогда
. Тогда 
• Рассмотрим непр. Х:
 •
•
№34 Закон больших чисел(теорема Маркова):
Опр: Говорят, что последовательность случ. величин  сходится по вероятности к числу a (
сходится по вероятности к числу a ( ), если
), если  ( или
( или 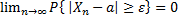 )
)
Теорема Маркова:
Пусть последовательность случ величин 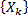 удовлетворяет условиям:
удовлетворяет условиям: 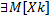 и
и 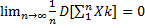 . Тогда
. Тогда  , т.е.
, т.е.  .
.
•Обозначим 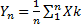 ,
,  ,
,  . Применяем второе неравенство Чебышева:
. Применяем второе неравенство Чебышева:
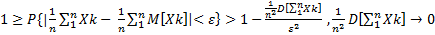 •
•
№35 Следствия из закона больших чисел
1) Теорема Чебышева
Пусть 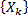 – последовательность независимых или попарно некоррелированных случ. величин(*).:
– последовательность независимых или попарно некоррелированных случ. величин(*).: 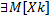 и
и 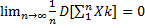 . Тогда Тогда
. Тогда Тогда 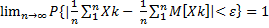
2) Пусть 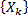 - последовательность одинаково распр. случ. величин, удовл. условию (*).
- последовательность одинаково распр. случ. величин, удовл. условию (*).
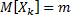 ,
, 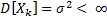 . Тогда
. Тогда 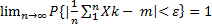 или
или 
3) Пусть  , т.е
, т.е 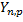 - число успехов в серии n испытаний в схеме Бернулли с вероятностью успеха p. Тогда
- число успехов в серии n испытаний в схеме Бернулли с вероятностью успеха p. Тогда 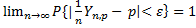 , т.е
, т.е 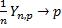
•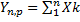
| Xk | ||
| p | q | p |

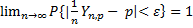 по следствию (2)•
по следствию (2)•
№36 Центральная предельная теорема
Опр: Пусть  - последовательность случайных величин. Говорят, что случайная величина
- последовательность случайных величин. Говорят, что случайная величина  имеет асимптотическое нормальное распределение с параметрами
имеет асимптотическое нормальное распределение с параметрами 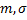 при
при 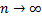 , если для
, если для 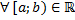
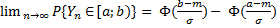 .
. 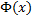 - функция Лапласа. Обозн:
- функция Лапласа. Обозн:  .
.
Теорема:
Пусть последовательность 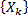 удовлетворяет условиям:
удовлетворяет условиям:
1) 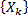 - независимы.
- независимы.
2) 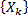 - одинаково распределены
- одинаково распределены
3) 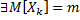 ,
, 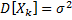
Тогда для  справедливо
справедливо  .
.
Замечания:
1)При достаточно больших n - 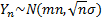 , т.е. сумма большого числа одинаково распределенных независимых случайных величин имеет распределение, близкое к нормальному.
, т.е. сумма большого числа одинаково распределенных независимых случайных величин имеет распределение, близкое к нормальному.
2) Условие (2) не является принципиальным. Если 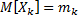 ,
, 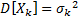 , то при некоторых требованиях вместо условия (3) при больших n имеем:
, то при некоторых требованиях вместо условия (3) при больших n имеем:
 ,т.е. и в этом случае сумма достаточно большого числа случайных величин распределена приблизительно нормально.
,т.е. и в этом случае сумма достаточно большого числа случайных величин распределена приблизительно нормально.
– Конец работы –
Эта тема принадлежит разделу:
Предмет теории вероятностей
На сайте allrefs.net читайте: "Предмет теории вероятностей"
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Дисперсия
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов